18 svar

55 visningar

Dkcre behöver inte mer hjälp

Skriv ett uttryck för

Hej

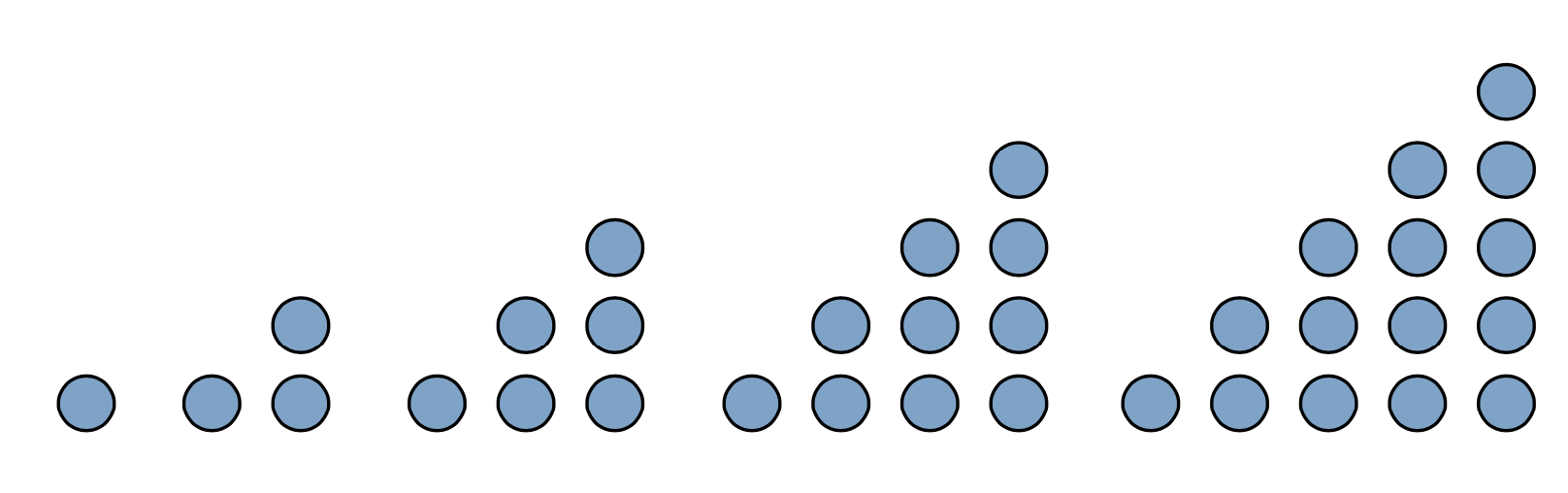
triangeltalen är 1,3,6,10,15

kvadrattalen är 1,4,9,16

a) skriv ett uttryck för n:te talet för respektive.

Mönstret för triangeltalen är att det ökar med befintligt tal sedan summan av alla tidigare tal i serien. Sen hur man skriver det matematiskt vet jag inte.

¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤

Ett uttryck för tredje talet exempelvis är 3 + (3-1) + (3-2) + (3-3)

Det verkar ju stämma faktiskt generellt :P

Är det såhär man gör? Vet inte varför summasymbolen blir konstig. Ser för övrigt att den är fel ändå med -1 där

$\sum_{n = 1}^{n} n + (n - 1)$

Här vill man ha enklare uttryck.

Du behöver undersöka talföljderna och hitta ett mönster.


Nr	$a_{n}$
1	$1 = 1 ²$
2	$4 = 2 ²$
3	$9 = 3 ²$
4	$16 = 4 ²$
5	$25 = 5 ²$

Kvadrattal: $a_{n} = n^{2}$

Jo.

Jag ser mönstret.

nr
1	1
2	3
3	6
4	10
5	15

Så det ökar med befintligt tal + summan av alla tidigare tal

En rekursiv formel för mönster du ser blir $a_{n + 1} = a_{n} + n$ .

Med de vill nog ha en sådan formel så att man inte behöver räkna alla tal före.

Kanske en bild kan hjälpa:

Jag vet inte vad jag ska säga.

Dom ökar enligt mönstret jag sa..

Diagonalen är lika lång som kateterna.

kvadraten av högsta stolparna minus talet innan är lika med nuvarande tal

K värdet är 1.

Tar man bort nuvarande nummer på talet på befintlig summa så får man resultatet av det tidigare talet

Hur kan man beräkna antalet prickar i en triangel utan att titta på föregående triangel?

Bra observation höjden på staplarna. Kan du titta på "bredden"?

Både höjden och bredden är lika som det tal man räknar, så för tal nummer 4 är det 4x4.

4x4 = 16, men resultatet ska vara 10. Så det ska bort nuvarande tal -2

Triangel 3 har mönstret 3x3 - n, dvs n(n-1)

på 4e då så n(n-1).. stämmer inte.

Dkcre skrev:
kvadraten av högsta stolparna minus talet innan är lika med nuvarande tal

Det här var också bra, men om man ska uttrycka det på ett matematiskt sätt så

${(n + 1)}^{2} - a_{n} = a_{n + 1}$

Kanske kan du förenkla uttrycket?

EDIT: Nej, tolkade det fel först ${(n + 1)}^{2} - a_{n} = (n + 1)$

MaKe skrev:
Dkcre skrev:
kvadraten av högsta stolparna minus talet innan är lika med nuvarande tal

Det här var också bra, men om man ska uttrycka det på ett matematiskt sätt så

${(n + 1)}^{2} - a_{n} = (n + 1)$

Kanske kan du förenkla uttrycket?

Nej jag kan utveckla kvadraten bara.

Kan man göra något av uttrycket jag skrev ovan och tidigare

$a_{n + 1} = a_{n} + (n + 1)$

OBS! Jag rättade uttrycket: ${(n + 1)}^{2} - a_{n} = a_{n + 1}$

Jag vet dock inte riktigt vad det där betyder ^^' jag lär kolla det först

n^2 +2n +1 - 1+ (n-1) * n

n^2+2n + (n-1)n

n^2+2n+n^2-n

2n^2+n

2n(n+1)

VL = 2n(n+1)

HL = 1+(n+1-1) * n

1+n^2

2n(n+1) = 1+n^2

2n^2 + 2n = n^2+1

n^2+2n = 1

-1n+-sqrt(1+1)

n = -1 $\pm$ $\sqrt{2}$

Sammanfattningsvis så, nej, jag kan inte förenkla det ^^'

Två uttryck för samma tal $a_{n + 1}$ .

${(n + 1)}^{2} - a_{n} = a_{n + 1} = a_{n + 1} = a_{n} + (n + 1) {(n + 1)}^{2} - a_{n} = a_{n} + (n + 1) {(n + 1)}^{2} - (n + 1) = 2 a_{n}$

Dubbelpost

Nej, jag begriper inte det här.

Men det bottnar i att man måste kunna titta på det där och sen identifiera mönstret och komma fram till att "ah, hey, så här är det".

Kollade upp svaret och jag hade ärligt talat aldrig identifierat det mönstret.

n(n+1)/2

¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤¤

I fråga b) här..

Så ska man undersöka summan av två på varandra följande triangeltal. Formulera en slutsats.

Slutsatsen jag kommer fram till att det är ett tal som går att kvadrera. Och dessutom att roten av det talet är lika med talnumret för det första talet i summering.

då i C) så ska detta bevisas, hur gör man det..

Tänker såhär:

$n (n + 1) / 2 + n (n + 1) / 2$

Men man måste då kunna särskilja på båda på något sätt, och ja.. kan man sätta in en variabel K = n+1 och placera i högra talet kanske?

${(n + 1)}^{2} - (n + 1) = 2 a_{n} a_{n} = \frac{n ² + 2 n + 1 - n - 1}{2} = \frac{n ² + n}{2} = \frac{n (n + 1)}{2}$

Dkcre skrev:
Men man måste då kunna särskilja på båda på något sätt, och ja.. kan man sätta in en variabel K = n+1 och placera i högra talet kanske?

$a_{k} = \frac{k (k + 1)}{2} k = n + 1 a_{n + 1} = \frac{(n + 1) (n + 2)}{2}$

Sedan lägger du ihop $a_{n} + a_{n + 1}$

MaKe skrev:
Dkcre skrev:
Men man måste då kunna särskilja på båda på något sätt, och ja.. kan man sätta in en variabel K = n+1 och placera i högra talet kanske?

$a_{k} = \frac{k (k + 1)}{2} k = n + 1 a_{n + 1} = \frac{(n + 1) (n + 2)}{2}$

Sedan lägger du ihop $a_{n} + a_{n + 1}$

Okej.. varför har man n+2 med där?

$a_{k} = a_{n + 1} = \frac{k (k + 1)}{2} = \frac{(n + 1) ((n + 1) + 1)}{2} = \frac{(n + 1) (n + 2)}{2}$

Det är ett uttryck för nästa tal, det måste ju bli större.

Tack

Svara

Visa senaste svar