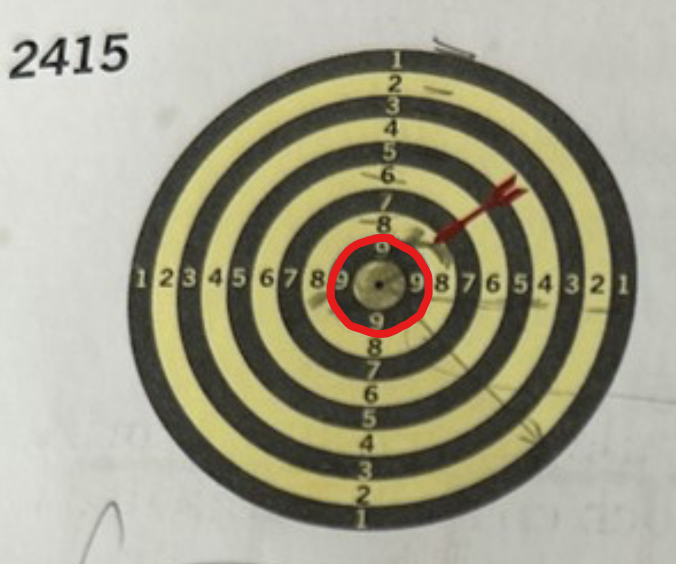
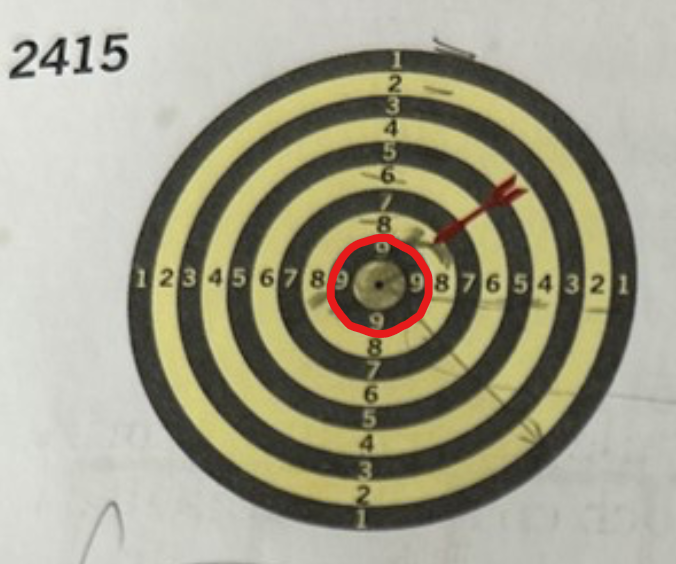
Skriv ett ett uttryck för arean

Hur gjorde du på a)?

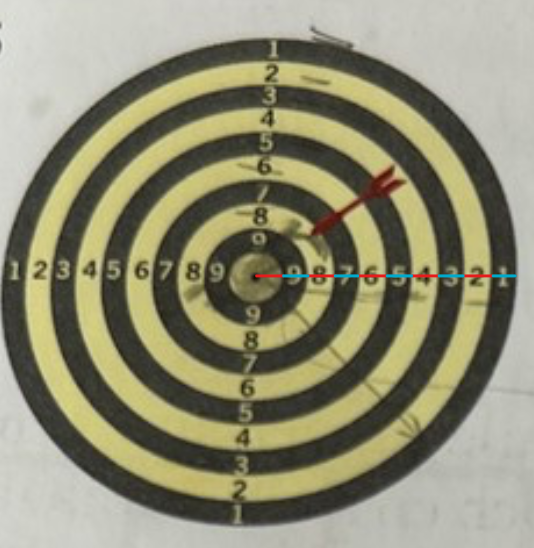
Okej. Hur stor radie har denna cirkel:

fner skrev:

Okej. Hur stor radie har denna cirkel:

A=ska man räkna roten ur sen a/pi=r?

Radien för 10p var $\frac{\sqrt{a/\pi }}{10}$. Radien för den röda cirkeln är dubbelt så stor, dvs $\frac{\sqrt{a/\pi }}{5}$. Kommer du vidare?

fner skrev:

Radien för 10p var $\frac{\sqrt{a/\pi }}{10}$. Radien för den röda cirkeln är dubbelt så stor, dvs $\frac{\sqrt{a/\pi }}{5}$. Kommer du vidare?

Men varför är det /5? förstår inte

Är du med på att den röda cirkelns radie är dubbelt så lång som radien för 10p-området?

fner skrev:

Är du med på att den röda cirkelns radie är dubbelt så lång som radien för 10p-området?

hur kan den vara dubbelt?

Troligtvis av samma anledning som varför du tog $\frac{\sqrt{a/\pi }}{10}$. Varför valde du 10 i nämnaren? Kanske kan denna bild hjälpa dig. Notera att de röda och de blå sträckorna är lika långa.

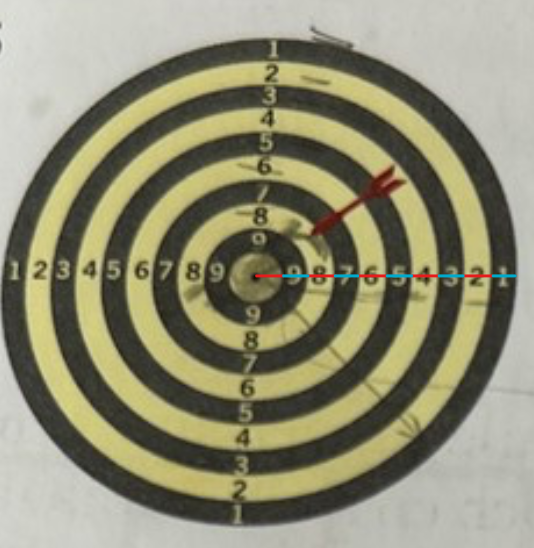
fner skrev:

Troligtvis av samma anledning som varför du tog $\frac{\sqrt{a/\pi }}{10}$. Varför valde du 10 i nämnaren? Kanske kan denna bild hjälpa dig. Notera att de röda och de blå sträckorna är lika långa.

för det stod 10 poäng:)

Okej, jag tror att jag förstår. Vi testar att tänka bakvägen: om vi säger att radien för 10p-ytan är x, vad är så radien för hela tavlan?

fner skrev:

Okej, jag tror att jag förstår. Vi testar att tänka bakvägen: om vi säger att radien för 10p-ytan är x, vad är så radien för hela tavlan?

är det så att hälften av 10 poäng är redien 5

Tänk bort poängen för ett tag. Vilka poäng som står på respektive område har ingenting med matematiken att göra. Det hade lika gärna kunnat stå 7 poäng längst ut och 50 innerst.

Det du behöver inse för att kunna lösa uppgiften är att alla cirklar har samma bandbredd, se inlägg #11. Att du delar med 10 och får rätt svar i inlägg #3 beror på att det finns tio olika områden med samma bandbredd, inte just att det är 10 poäng i mitten. Om radien för 10p är x så är radien för hela tavlan 10x. Du räknade att radien för hela tavlan var r och att radien för 10p var r/10, vilket går lika bra!

fner skrev:

Tänk bort poängen för ett tag. Vilka poäng som står på respektive område har ingenting med matematiken att göra. Det hade lika gärna kunnat stå 7 poäng längst ut och 50 innerst.

Det du behöver inse för att kunna lösa uppgiften är att alla cirklar har samma bandbredd, se inlägg #11. Att du delar med 10 och får rätt svar i inlägg #3 beror på att det finns tio olika områden med samma bandbredd, inte just att det är 10 poäng i mitten. Om radien för 10p är x så är radien för hela tavlan 10x. Du räknade att radien för hela tavlan var r och att radien för 10p var r/10, vilket går lika bra!

jaha nu förstod jag

Kommer du vidare och kan lösa uppgiften då?

fner skrev:

Kommer du vidare och kan lösa uppgiften då?

Jag ska väl göra samma sak som på a men dela på 5 eller?

Ja. Men kan du förklara varför du delar på 5?

fner skrev:

Ja. Men kan du förklara varför du delar på 5?

För att hela i mitten av cirklen är det 10 poäng och jag behöver ta reda på vad radien är på halva den så jag delade med 2 =5. 

Nja jag är inte riktigt med är. Radien för 10p-området har du ju redan beräknat till √(a/π)/10. Denna radie kan du inte dela på 2 för att få radien för 9p- OCH 10p-området (se inlägg #4).

fner skrev:

Nja jag är inte riktigt med är. Radien för 10p-området har du ju redan beräknat till √(a/π)/10. Denna radie kan du inte dela på 2 för att få radien för 9p- OCH 10p-området (se inlägg #4).

2(rotenur a/10) eller?

Ja! Jippi! Glöm inte pi i uttrycket bara, men du ser ju hur du har skrivit i ditt räknehäfte i a)-uppgiften :)

fner skrev:

Ja! Jippi! Glöm inte pi i uttrycket bara, men du ser ju hur du har skrivit i ditt räknehäfte i a)-uppgiften :)

ja! tack så mycket för hjälpen!