Skissa x^2-y^2-z^2=4
Har förstått enligt boken att formen är en hyperboloid med två "separata sidor" där den negativa termen dikterar åt vilken axel hyperboloid ska "ligga åt", sorry terminologin är kass.
Jag börjar med att skriva om ekvationen till eftersom jag vill ha en faktor negativ (x^2), och detta säger mig att vi ska ligga på x-axeln. Sen skissar jag två skål-liknande figurer med start i x=+-2 eftersom y,z=0 där. Räcker det? jag vet inte hur "tät" skålen ska vara osv. Förväntas något mer av mig? läser flerdimensionell analys.
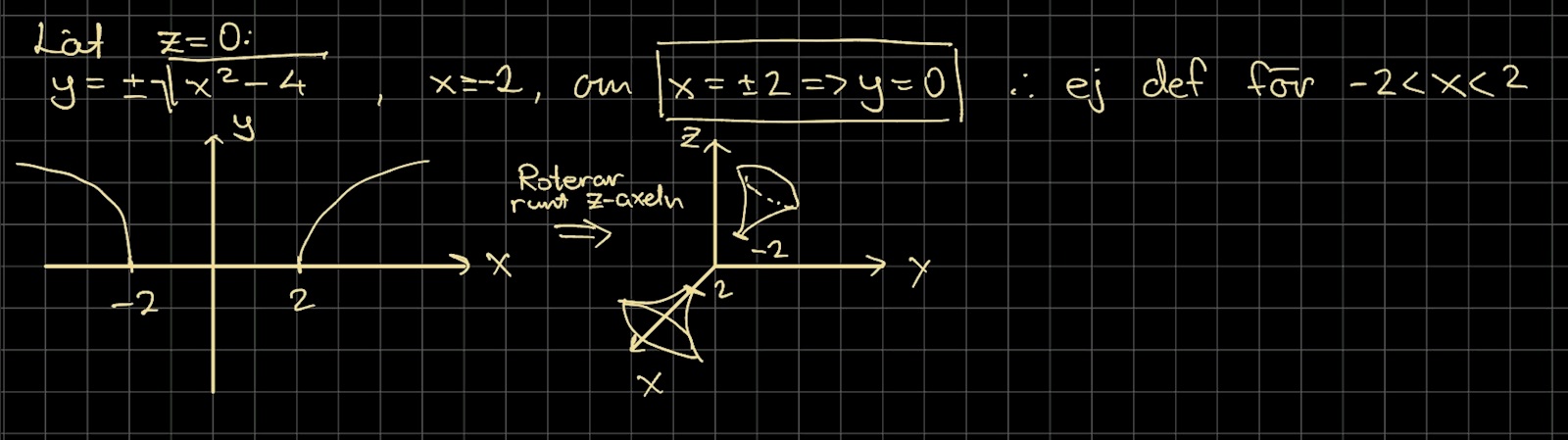
Om man inte vill försöka rita nåt tredimensionellt kan man rita en projektion av hyperboloiden på t.ex. x-z-planet och sedan är det bara att rotera det hela runt z-axeln (alltså att skriva att man gör det, så får betraktaren föreställa sig det).
Det borde duga, tycker jag.
Laguna skrev:Om man inte vill försöka rita nåt tredimensionellt kan man rita en projektion av hyperboloiden på t.ex. x-z-planet och sedan är det bara att rotera det hela runt z-axeln (alltså att skriva att man gör det, så får betraktaren föreställa sig det).
Det borde duga, tycker jag.
Okej så du menar något sånt här? var faktiskt mycket lättare på detta sättet, tack för tipset :)