Skissa kurvan

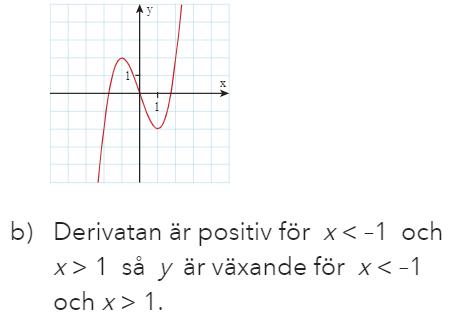
Själv har jag gjort så här:
Först tar jag derivatan av funktionen
Sen låter jag y'=0 för att undersöka extrempunkter
Detta betyder att vid x-värden 1 och -1 är derivatan lika med 0.
Sen förstår jag det som att jag kan göra en av två metoder:
Metod 1 är att undersöka derivatans lutning vid punkter till vänster och höger av extrempunkterna 1 och -1. Alltså:
x=1 har negativ lutning till vänster och positiv till höger, så är en minimipunkt.
x=-1 har positiv till vänster och negativ till höger, så är en maximipunkt.
Metod 2 är att istället bara ta andraderivatan för x=1 och x=-1 för att se vilka sorts extrempunkter de är.
x=1 ger en positiv värde och är därför en minimipunkt.
x=-1 ger en negativ värde och är därför en maximipunkt.
Jag har några frågor.
- Hur går jag vidare från här? Är det bara att göra en värde tabell eller finns det ett bättre sätt?
- Vilket av de två metoderna borde man använda? Är det så att man använder metod 2 (andraderivatan) om man kan (som i ) och att man använder metod 1 när man inte kan använda andra derivatan (som i t.ex. )?
- Och hur fick de y-koordinaten (-1,2) och (1,2) i lösningen som jag visade där uppe? Har de bara glömt att visa hur de gjorde eller är det så lätt att det inte behövs visa?
Tompalomp skrev:Jag har några frågor.
- Hur går jag vidare från här? Är det bara att göra en värde tabell eller finns det ett bättre sätt?
Om du enbart vill skissa grafen grovt så behöver du inte ta fram en värdetabell, men du bör ta reda på minimi- och maximipunktens y-koordinater för att kunna pricka in dem rätt.
Dessutom är det bra att pricka in eventuella nollställen, så att lösa ekvationen f(x) = 0 är praktiskt.
Du kan läsa mer om att skissa grafer här.
- Vilket av de två metoderna borde man använda? Är det så att man använder metod 2 (andraderivatan) om man kan (som i ) och att man använder metod 1 när man inte kan använda andra derivatan (som i t.ex. )?
Ja det är en bra taktik. Ibland (som här) är det väldigt enkelt att ta fram andrderivatan och då är det att föredra, speciellt som det ger färre beräkningar.
- Och hur fick de y-koordinaten (-1,2) och (1,2) i lösningen som jag visade där uppe? Har de bara glömt att visa hur de gjorde eller är det så lätt att det inte behövs visa?
Minimipunkten har koordinaterna (1, f(1)). Vi har att f(1) = 13-3•1 = -2.
Maximipunkten har koordinaterna (-1, f(-1)). Vi har att f(-1) = (-1)3-3•(-1) = 2.
Okej, tror jag fattar. Om jag skulle lägga upp det i steg så att jag lättare kommer ihåg blir det alltså
- derivera [f'(x)]
- ställ derivatan lika med noll [f'(x)=0] och beräkna x, för att hitta extrempunkter
- ta andraderivatan och lägg in svaret på x [f''(1)], för att veta om de är max, min, eller terasspunkter
- sätt in svaret på x i vanliga funktionen [f(x)], för att hitta vilken y-koordinat punkterna har
- hitta eventuella nollställen för funktionen genom att sätta funktionen lika med noll och beräkna x [f(x)=0]
- skissa grafen
Och om jag vill ha en mer exakt graf gör jag ett värde tabell.
Är detta en okej guide att komma ihåg?
Och, för denna problem, är väl detta korrekt sätt att hitta nollställena?
Alltså kommer denna funktion skära x-axeln vid punkterna x=1,73 och x=-1,73?
Tompalomp skrev:Okej, tror jag fattar. Om jag skulle lägga upp det i steg så att jag lättare kommer ihåg blir det alltså
- derivera [f'(x)]
- ställ derivatan lika med noll [f'(x)=0] och beräkna x, för att hitta extrempunkter
Ja, fast om vi ska vara petiga så hittar du de stationära punkterna (dvs de punkter där derivatan är lika med 0) på detta sättet. En terrasspunkt är en stationär punkt men inte en extrempunkt.
- ta andraderivatan och lägg in svaret på x [f''(1)], för att veta om de är max, min, eller terasspunkter
- sätt in svaret på x i vanliga funktionen [f(x)], för att hitta vilken y-koordinat punkterna har
- hitta eventuella nollställen för funktionen genom att sätta funktionen lika med noll och beräkna x [f(x)=0]
- skissa grafen
Och om jag vill ha en mer exakt graf gör jag ett värde tabell.
Är detta en okej guide att komma ihåg?
Utöver kommentaren ovan så ser det jättebra ut.
Tompalomp skrev:
Du tappar bort en lösning när du dividerar med x.
Gör så här:
Faktorisera:
Enligt nollproduktmetoden har ekvationen lösningar där och där , dvs vid , och
Ahhh, okej! Fattade inte det. Så ta alltså aldrig bort ett x i funktionen för att alla x representerar ett svar?
Tompalomp skrev:Ahhh, okej! Fattade inte det. Så ta alltså aldrig bort ett x i funktionen för att alla x representerar ett svar?
Ja, eller snarare, du bör aldrig (utan resonemang) dividera en ekvation med en faktor som kan ha värdet 0.
Detta eftersom du då tappar bort informationen om att detta är en möjlig lösning till ekvationen.
====================
Exempel:
x2-4 = x-2
Om vi nu faktoriserar vänsterledet enligt konjugatregeln så får vi
(x-2)(x+2) = x-2
Om vi nu dividerar båda sidor med x-2 får vi x+2 = 1 med lösningen x = -1. Vi har nu tappat bort informationen om att även x = 2 är en lösning till ekvationen.
======================
Jag skriver "utan resonemang" eftersom en alternativ metod att lösa ekvationen är att först faktorisera vänsterledet enligt ovan och sedan resonera kring fortsättningen, ungefär så här:
"Vi har (x-2)(x+2) = x-2
Vi kan nu dela upp ekvationen i två fall:
- x-2 = 0, dvs x = 2. Ekvationen är då uppfylld, vilket betyder att x = 2 är en lösning.
- x-2 0, dvs x 2. Vi kan då dividera hela ekvationen med x-2 och vi får då x+2 = 1, dvs x = -1.
Ekvationen har alltså lösningarna x = 2 och x = -1".
==============
Men det är enklare och snyggare att använda nollproduktmetoden enligt kommentar #6.
Nice! Tack för förklaringen!



