skissa grafen till en fuktion
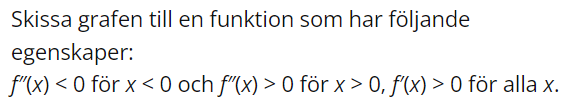
Jag är inte säker på om jag ritade det rätt
Nästan.
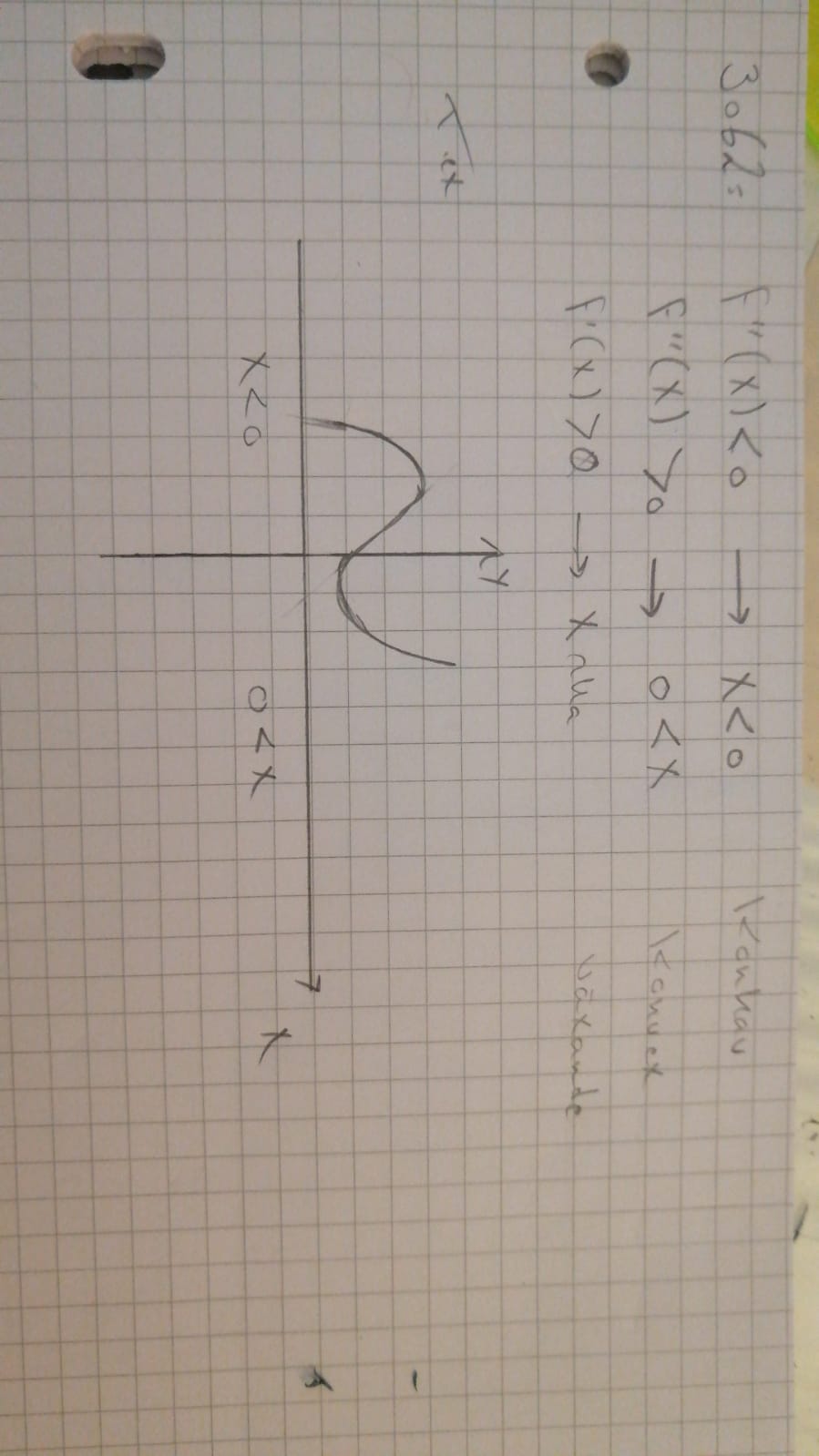
Din graf uppfyller de båda villkoren för andraderivatan, men inte det för förstaderivatan eftersom grafen har negativ lutning nära y-axeln.
Fundera lite till och fråga efter tips om du inte kommer vidare.
Hur vet man att grafen har negativ lutning nära y-axeln?
Blå - uppförsbacke - positiv lutning - f'(x) > 0
Röd - nerförsbacke - negativ lutning - f'(x) < 0
Förtydligande: Din graf har negativ lutning nära y-axeln, men den graf du ska rita ska ha positiv lutning överallt.
Jag har fastnat på den här frågan.
Jag vet att f'(x) > 0 betyder att funktionen växande, men jag vet inte hur ska komma vidare
Du kan tänka så här: Det är bara i den röda delen av grafen som f'(x) < 0, överallt annars uppfylls alla villkor. Går det att få bort den röda delen pä något sätt?
Nu fattar jag. Den röda delen är f'(x) < 0 vilket innebär att funktionen avtagande. Medan funktionen som jag måste skissa måste vara växande.
Just det.
Du ska ha f'(x) > 0 överallt, dvs funktionen ska vara växande överallt, dvs grafen ska ha "uppförsbacke" överallt, dvs grafen ska ha positiv lutning överallt.
Som i de blåa partierna av din graf.
Yes, tack för hjälpen :)
Visa gärna ditt resultat, det hjälper andra som kämpar med samma fråga.
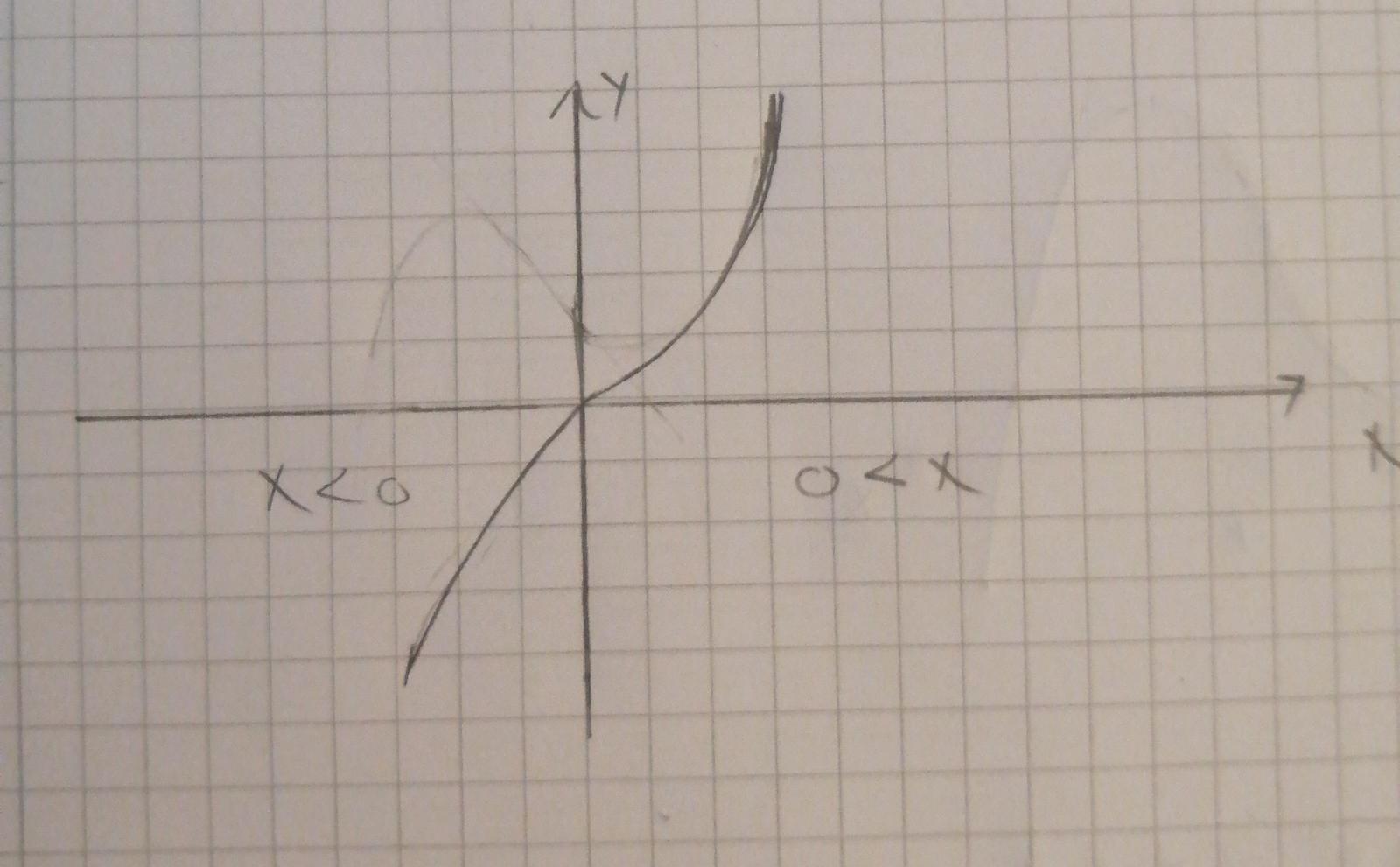Grafen ska vara ungefär så här:
Snyggt!
