Skillnad på transversalsatsen och topptriangelsatsen
Jag undrar vad skillnaden mellan transversalsatsen och topptriangelsatsen är, och när man ska använda vilken utav dem?
Om vi har en triangel som denna:
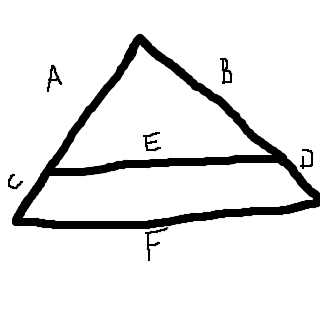
Och vi har sidorna A, B och C, och vill bestämma D, då kan transversalsatsen användas. Om E eller F ska beräknas, alternativt finns med i beräkningen, måste topptriangelsatsen användas.
Topptriangelsatsen säger att: .
Transversalsatsen säger i stort sett att .
Jag förstår inte vad skillnaden mellan dem två är av att läsa den texten. Finns det en konkret skillnad i vad dem används för?
Egentligen kan man säga att topptriangelsatsen är bara vanlig likformighet, sidorna i den lilla triangeln förhåller sig som sidorna i den större triangeln.
Transversalsatsen däremot handlar om att de sidor som tranversalen skär delas upp med samma förhållande.
Vilken man skall använda är helt en fråga om vilken sida man letar efter och vilka sidor man har givna.
Jag föredrar att inte använda någondera, utan resonera från likformighet.




