Skillnad mellan två integraler
Undrar bara om det finns något snabbt sätt å tänka eller se hur man vet vilken av integralerna man ska ha först när man ska beräkna differensen mellan dessa så att man inte får en negativ volym?

får ej använda räknare så om det går att snabbt föreställa sig kurvorna på något sätt? Istället för att. 50-50 chans att man väljer rätt först
Om du ritar upp området, får du något i denna stil:
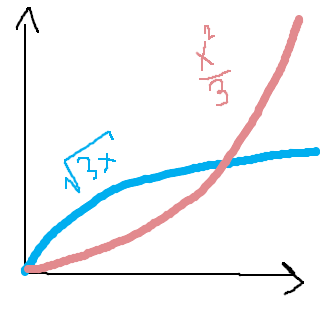
Du måste hitta skärningspunkterna, men när du gjort det, kan du ta något x = a (där a ligger mellan skärningen) och hitta och . Den som har störst värde ligger överst. :)
Smutstvätt skrev:Om du ritar upp området, får du något i denna stil:
Du måste hitta skärningspunkterna, men när du gjort det, kan du ta något x = a (där a ligger mellan skärningen) och hitta och . Den som har störst värde ligger överst. :)
Okej okej men hur ska man veta att dom ser ut sådär dom r kurvorna? Är det nått man vet eller räknar man på det?
Hej!
Du skulle kunna göra en tabell för varje funktion. Sedan vet du att x^2 är en "glad mun", och (x^2)/3 är ju (1/3)*x^2. Vet inte om detta hjälper, men lycka till i alla fall!
/Pluggasmart
Maremare skrev:
Okej okej men hur ska man veta att dom ser ut sådär dom r kurvorna? Är det nått man vet eller räknar man på det?
Om du är van att skissa grafer så vet du hur en -graf och en -graf ser ut.
Graferna i denna uppgift har samma principiella utseende.
Börja med att ta reda på skärningspunkterna.
Då kan du rita en "-liknande" och en "-liknande" graf som går genom dessa gemensamma punkter.
Egentligen spelar det ingen roll om din skiss är verklighetstrogen eller inte, den är bara ett tankestöd.
Som redan nämnts är det viktigaste är att du hittar skärningspunkterna samt att du vet vilken graf som är ovanför den andra i det aktuella intervallet.
Man kan väl bara köra på, och om svaret blir negativt så byter man tecken. Om man kan motivera trovärdigt vad man gör för något borde det väl bli godkänt, men jag kan inte lova det.
"Snabbt sätt att tänka"?
De bägge funktionerna sägs ju begränsa ett område, dvs ha två begrränsningslinjer i x. Ett x-värde för begränsningen skulle kunna vara 0. Dock vet du ej om den andra begränsningen i x ligger till vänster eller höger om origo. Men roten ur negativa tal är knepigt så om du är övertygad att nästa begränsande värde för x >= 0, så borde borde du kunna studera derivatan på respektive funktion i x = 0 och välja den med större derivata som första term. Du vet att funktionerna så småningom möts igen med större x.
Jag skulle nog också rita en figur ungefär som Smutstvätt beskriver






