Skillnad mellan ett uttryck och en ekvation (Matematik/Årskurs 8)

Ekvation betyder likhet, så en ekvation har alltid ett likhetstecken.

Om du kör 70 km i timmen, och mäter tiden (t) i timmar och sträckan (s) i kilometer kan man skriva ekvationen:

s = 70t

Du kan också skriva ett uttryck för hur lång sträcka du har kört efter tiden t. Det ser ut så här:

70t

Ett uttryck är en bit matematisk soppa, exempelvis $5 x + 3$ eller $7 y + x^{2} - \frac{6}{7}$ . Oftast brukar uttrycken ha någon representation i verkligheten, därav namnet, men rent definitionsmässigt kan det vara nästan vilka matematiska krumelurer som helst. Titta på denna bild:

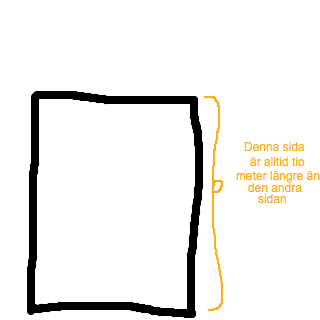
Om vi nu vill variera den övre sidan, kan det vara smart att döpa den till något enkelt, exempelvis x. Vi kan då sammanfatta den andra sidans area med uttrycket $x + 10$ . Vi kan även skriva ett uttryck för arean: $x (x + 10)$ .

Om vi däremot vill räkna ut exakt vad någonting är, måste vi ju veta hur stor den andra sidan är, eller hur stor arean är, om vi ska kunna räkna ut sidornas längd. Då kanske vi vet att rummet som vi ska lägga golvet i har en area på 75 kvadratmeter. Då sätter vi vårt uttryck lika med ett värde, $x (x + 10) = 75$ . Nu har vi en ekvation, och kan härifrån räkna ut hur golvets sidor ska vara. Det finns ett specifikt svar, och inget annat (vissa ekvationer kan ha flera lösningar, men ändå). En ekvation är alltså en matematisk soppa som har någon slags begränsningar (i det andra ledet).

För att sammanfatta: Både uttryck och ekvationer är matematisk soppa. Skillnaden är att uttryck beskriver, medan ekvationer bestämmer/beräknar.

Okej då! Tack Smutstvätt

En tredje infallsvinkel är vad det betyder.

En ekvation är ett påstående, i form av en fullständig mening. Eftersom ett påstående antingen är sant eller falskt så har en ekvation alltså två möjliga värden, nämligen SANT eller FALSKT.

Exempel: Ekvationen 3x = 9 är ett påstående, nämligen "3 multiplicerat med x är lika med 9". Detta påstående är SANT om x har värdet 3 men FALSKT vid alla andra värden på x. Vi säger att ekvationen är SANN (uppfylld) om x är lika med 3 och FALSK (ej uppfylld) om x har något annat värde än 3.

----------

Ett uttryck däremot kan inte översättas till en fullständig mening utan är närmast att betrakta som en satsdel. Ett uttryck kan ofta anta flera olika värden, beroende på värdet hos uttryckets beståndsdelar.

Exempel: Uttrycket 3x kan översättas till "3 multiplicerat med x", vilket inte är en fullständig mening. Uttrycket 3x antar olika värden beroende på vad x har för värde.

Okej Yngve, tack!

Tack SvanteR!

Vet att tråden är löst men gör mitt inlägg informella/formell terminologi då jag tycker att det finns ett värde i att ibland kunna skilja på olika typer av uttryck

Uttryck: Någon i sammanhanget acceptabel kombination av symboler.

Okej det är aningen abstrakt så låt oss istället gå igenom några specifika typer av uttryck:

Aritmetiskt uttryck: Någon kombination av kända tal; {0,1,-6, (3,221), $\pi$ ,...} och aritmetiska operationer { $+,-,\cdot, /$ , potenser, n-rötter}

Exempel: $(1 +2)\cdot 3 + \frac{4}{5} -6$

Aritmetiska uttryck beskriver hur man går till väga för att från de involverade talen 1,2,3,4,5 och 6 producera ett nytt tal. I detta fall 3,8 (alternativt uttryckt 19/5)

Ett aritmetiskt uttryck måste dock vara 'grammatiskt rimligt' då knasiga kombinationer såsom

$\frac{3 -4}{+} - \cdot + \frac{-}{5}$ visserligen är en kombination av de relevanta symbolerna men detta är inte ett aritmetiskt uttryck. Likt hur "är jag går när hus du" inte är en giltig mening även om det är en kombination av ord.

Algebraiskt uttryck: Någon kombination av kända tal; {0,1,-6, (3,221), $\pi$ ,...} och aritmetiska operationer, och symboler {x,y,z,a,b,\gamma} vilka representerar eventuellt okända värden.

Samma sak som aritmetiska uttryck men där vi även involverar symboler som representerar tal

$2x + 3(5 - a) - \frac{4}{x +y}$

Algebraiska uttryck beskriver hur man skulle kunna gå till väga för att kombinera tal om man kände till dem. SvanteRs exempel med 70t som ett uttryck som kunde användas för att beräkna hur långt bilen kört om man kände till värdet på t är ett exempel på detta. (Åter så måste kombinationen vara 'grammatiskt rimlig')

Analytiska/Matematiska uttryck: Likt algebraiska uttryck men i princip tillåtandes alla tänkbara operationer som kända funktioner, gränsvärden eller rent formella uttryck som "1 + (-1) + 1 + (-1) + 1 + (-1) + ...". Vart man drar gränser här överkurs att beskriva.

Alla dessa typer av objekt kan man hänvisa till som uttryck.

Ekvation: Två uttryck med en mellanliggande likhet som uttrycker att två processer ger samma resultat.

$2x + 3 = 1$ , är en ekvation med uttrycken "2x + 3" och "1"

$(4x +1)^3 = \frac{\pi}{2}$ , är en ekvation med uttrycken $(4x +1)^3$ och $\frac{\pi}{2}$

Även 1 + 3 = 2 + 2 är tekniskt sett en ekvation med uttrycken "1 + 3" och "2 + 2" även om man främst brukar använda ekvationsbegreppet när det finns i alla fall en okänd 'x' i något av uttrycken.

En ekvation beskriver att två processer producerar samma resultat om man utför dem, ett resultat som kan användas för att lista ut vad de okända värdena är för något.

En särskillt typ av ekvationer kallas även vid ett separat namn:

Identitet: En ekvation som är sann oavsett vilka värden de okända har.

$x + x = 2x$ , stämmer oavsett om x är 0,1,5,1001, eller vadsomhelst. Processerna av att addera två lika tal eller multiplicera ett tal med 2 ger båda samma resultat.

$$x + 1 = 2$$ är inte en identitiet eftersom det endast stämmer om x = 1 men inte för x = 2.