#skärningspunkter av kordor inuti en cirkel=nCr(n,4)*
Hej!
*Om man delar upp en cirkel i ekvidistanta punkter längs med randen, drar alla kordor mellan punkterna och tillåter att det aldrig går tre kordor genom samma punkt ges antalet skärningspunkter mellan kordorna inuti en cirkel av
Jag förstår att detta beror på att man väljer ut två par man ska dra kordor emellan, och således får antalet möjligheter att ta fram punkter där två kordor korsas.
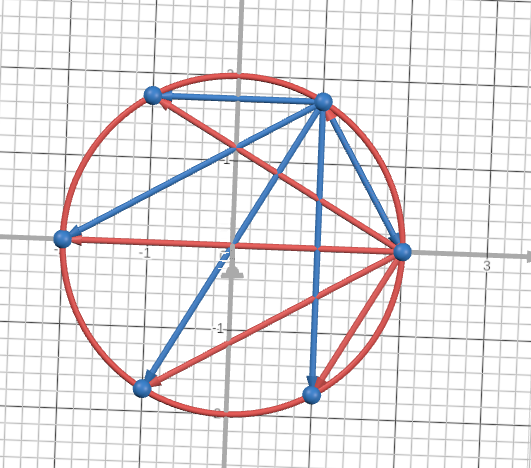
Det jag inte riktigt förstår är varför det räcker att bara titta på antalet sätt att välja ut 4 punkter? Här har jag ritat upp en cirkel med lite fler kordor än bara 2 kordor (alltså mellan 4 punkter), och det finns fortfarande inte fler än 3 skärningar mellan några kordor:
Jag förstår din fråga men förstår inte ditt exempel.
Om vi då börjar med din fråga, det här är ett bijektionsbevis. Vi löser uppgiften genom att visa att det existerar en bijektion mellan mängden vars element vi vill räkna och en annan mängd vars antal element är enkelt att beräkna.
Så, vi vill räkna antalet skärningspunkter. Betrakta en skärningspunkt mellan två kordor. De två kordorna bestämmer en mängd av 4 punkter på cirkelns periferi.
Omvänt: välj 4 punkter på cirkelns periferi. De bestämmer entydigt en punkt inuti cirkeln, där kordorna skär varandra.
Så vi har en funktion från skärningspunkter mellan kordor och mängder av storlek 4 av punkter på periferin. Villkoret att tre kordor aldrig går genom samma punkt ger att funktionen är 1 till 1.
Antalet mängder av 4 punkter på periferin är känt, det är n över 4.
Hjälper den förklaringen?
Smutsmunnen skrev:Jag förstår din fråga men förstår inte ditt exempel.
Om vi då börjar med din fråga, det här är ett bijektionsbevis. Vi löser uppgiften genom att visa att det existerar en bijektion mellan mängden vars element vi vill räkna och en annan mängd vars antal element är enkelt att beräkna.
Så, vi vill räkna antalet skärningspunkter. Betrakta en skärningspunkt mellan två kordor. De två kordorna bestämmer en mängd av 4 punkter på cirkelns periferi.
Omvänt: välj 4 punkter på cirkelns periferi. De bestämmer entydigt en punkt inuti cirkeln, där kordorna skär varandra.
Så vi har en funktion från skärningspunkter mellan kordor och mängder av storlek 4 av punkter på periferin. Villkoret att tre kordor aldrig går genom samma punkt ger att funktionen är 1 till 1.
Antalet mängder av 4 punkter på periferin är känt, det är n över 4.
Hjälper den förklaringen?
Ja, det hjälper, tack.
Det jag tänkte var att när vi räknar och är antalet punkter, så räknar vi ut hur många sätt vi kan välja ut fyra punkter från mängden av punkter. Det motsvarar antalet sätt att välja ut en skärningspunkt (fyra punkter motsvarar en skärningspunkt), men drar man alla kordor inuti en cirkel finns det ju fler skärningspunkter än en. Förstår du då vad min förvirring ligger?
Ignorera mitt exempel, jag insåg att jag inte ritat ut alla kordor.
Det känns som att du tänker fel nu, det är inte fråga om antalet sätt att välja 1 skärningspunkt (även om vi skulle kunna formulera beviset så men det är inte nödvändigt).
Utan antalet skärningspunkter=antalet sätt att välja fyra punkter på periferin.
Beviset är att det finns en 1-1 funktion från skärningspunkterna till delmängder av storlek 4 av punkter på periferin.
Jag fattar att det blir lite snurrigt i huvudet om man tänker som du gjort nu, i och för sig är antalet sätt att välja en skärningspunkt = antalet skärningspunkter (typ om det sitter 3 personer i ett rum så finns det 3 sätt att välja en person i det rummet men det är ett konstigt sätt att uttrycka att det sitter 3 personer i rummet).
Smutsmunnen skrev:Det känns som att du tänker fel nu, det är inte fråga om antalet sätt att välja 1 skärningspunkt (även om vi skulle kunna formulera beviset så men det är inte nödvändigt).
Utan antalet skärningspunkter=antalet sätt att välja fyra punkter på periferin.
Beviset är att det finns en 1-1 funktion från skärningspunkterna till delmängder av storlek 4 av punkter på periferin.
Jag fattar att det blir lite snurrigt i huvudet om man tänker som du gjort nu, i och för sig är antalet sätt att välja en skärningspunkt = antalet skärningspunkter (typ om det sitter 3 personer i ett rum så finns det 3 sätt att välja en person i det rummet men det är ett konstigt sätt att uttrycka att det sitter 3 personer i rummet).
Ah ja, det blir ju lite snurrigt för det finns en spännande hopkoppling mellan skärningspunkterna och kordorna.
Jag faktiskt hittade en video som de första fem minutrarna går igenom exakt detta problem:
https://www.youtube.com/watch?v=YtkIWDE36qU
Den, tillsammans med din förklaring, hjälpte mig. Tack!

