Skärningspunkter andragradsekvationer
Hej! Jag behöver hjälp med denna uppgift!
För funktionerna f och g gäller att f(x)=x2+a .
Antalet skärningspunkter mellan funktionernas grafer beror på hur konstanterna a och b väljs.
Undersök hur antalet skärningspunkter beror på valet av a och b.
Jag försökte rita ut olika alternativ:
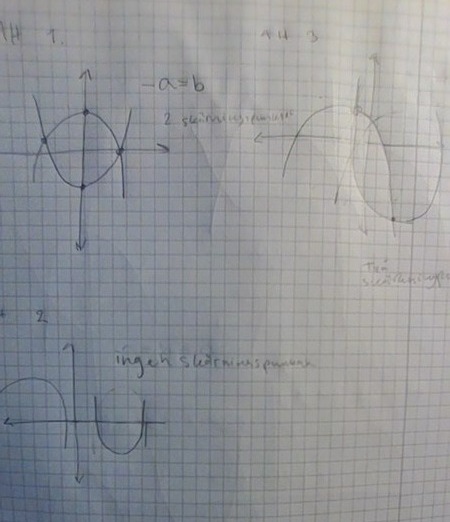
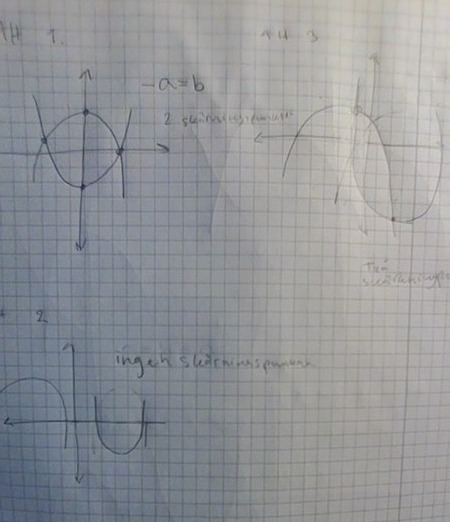
men jag tycker inte riktigt att jag kommer fram till någon specifik slutsatts.
Först tänkte jag att om a och b är likamed 0 innebär det att funktionerna inte har en skärningspunkt i y axeln. Då ritade jag alternativ 2. Men det stämmer ju inte, extrempunkten ska ju vara i origo om c=0 i en andragradsfunktion(dvs ax^2+bx+c). Så hur får graferna inga skärningspunkter med y-axeln(eller inga skärningspunkter med varandra)? Eller får de alltid det då de växer i all oändlighet? Men i såfall har väll graferna alltid två skärningspunkter?
Tack för hjälpen i förhand! Denna typen av frågor har förvirrat mig länge så är tacksam för all hjälp!
Jumsan_j skrev:Hej! Jag behöver hjälp med denna uppgift!
För funktionerna f och g gäller att .
Antalet skärningspunkter mellan funktionernas grafer beror på hur konstanterna a och b väljs.Undersök hur antalet skärningspunkter beror på valet av a och b.
Jag försökte rita ut olika alternativ:
men jag tycker inte riktigt att jag kommer fram till någon specifik slutsatts.
Först tänkte jag att om a och b är likamed 0 innebär det att funktionerna inte har en skärningspunkt i y axeln.
Alla andragradsfunktioner har en skärningspunkt med y-axeln - de har ju ett värde om man stoppar in att x = 0 i funktionen!
Då ritade jag alternativ 2. Men det stämmer ju inte, extrempunkten ska ju vara i origo om c=0 i en andragradsfunktion(dvs ax^2+bx+c).
Nej, extrempunkten för den funktionen ligger där x = -p/2, om vi använder de beteckningar som brukar användas i pq-formeln, för att inte blanda ihop dem med konstanterna a och b i den här uppgiften. Men i det här fallet är det p i din funktion/ekvation som är 0, och då stämmer det att extrempunkten ligger på y-axeln. I din bild 2 har ingen av funktionerna p = 0, d v s ingen av dem stämmer med funktionerna i uppgiften.
Så hur får graferna inga skärningspunkter med y-axeln(eller inga skärningspunkter med varandra)?
Det är två olika frågor - en andragradsfunktion har alltid en skärning med y-axeln, men det är inte säkert att två andragradsfunktioner korsar varandra.
Eller får de alltid det då de växer i all oändlighet?
Den ena kurvan växer oändligt mycket uppåt och har en minimipunkt, den andra väser oändligt mycket neråt och har en maximipunkt. Ibland korar de varandra, ibland inte, det är detta du skall undersöka.
Men i såfall har väll graferna alltid två skärningspunkter?
Nej.

Tack för hjälpen i förhand! Denna typen av frågor har förvirrat mig länge så är tacksam för all hjälp!
Jahhaa jag tror jag förstår, hade visst missupfattat vissa koncept lite!
isåfall tänker jag såhär:
stämmer det? Tack för hjälpen!
Det verkar stämma.
Det är ofta så att det är svårare att förså vad det är man frågar efter än det är att lösa själva uppgiften!