Sista versen beträffande tvåpolssatsen
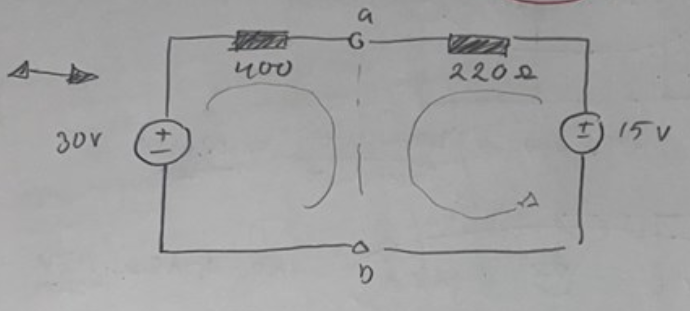
Bedyrar att jag ska sluta tjata om tvåpolsatsen och gå vidare, men vill bara försöka förstå fråga f också. Detsamma gäller som vid de tidigare tillfällen, man ska förenkla kretsen och lösa ut e(V) och Rt. Jag antar att jag kanske bör gå tillbaka till grunderna och repetera (vilket jag kommer göra oavsett). Vad som förvirrar mig i detta problem är ju att a och b sitter inbyggda i kretsen. Samt blir det nog fel någonstans när jag försöker avgöra vilka kretsar som är parallella/i serie med varandra. Mina svar är givetvis felaktig, är ju därför jag kommer hit :) men det kanske kan ge en hint om min tankegång. Jag har delat upp min lösning i 4 steg och jag tror att det är på det fjärde steget allt går käpprätt och skogen (kan givetvis vara tidigare också…).
Jag har även försökt lösa steg 4 på ett alternativ sätt genom att försöka laborera lite annorlunda med resistorerna. Samt undrar jag också om det är nödvändigt att använda KVL?
I vilket fall har jag nog aldrig varit med om digrar hjärngympa men sjukt kul är det ändå!
Mvh,
Archie



Visa spoiler
Skriv ditt dolda innehåll här
Jag tycker ditt andra alternativ ser bra ut men stanna här:
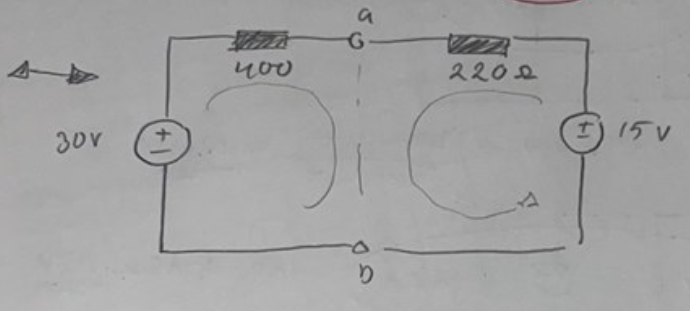
Här kan du räkna ut Uab i obelastat tillstånd.
Sen har du räknat ut vilka strömmar som flyter i a-b när man kortsluter. Du summerar strömmarna från vardera spänningskällan och får sedan Rut = Uab/Itot
ThomasN skrev:Jag tycker ditt andra alternativ ser bra ut men stanna här:
Här kan du räkna ut Uab i obelastat tillstånd.
Sen har du räknat ut vilka strömmar som flyter i a-b när man kortsluter. Du summerar strömmarna från vardera spänningskällan och får sedan Rut = Uab/Itot
Varmt tack! Jag har dock lite svårt att förstå hur jag ska beräkna Uab i obelastat tillstånd? Men jag gick vidare på detta sätt. (Avrundat, blir svaren rätt, men det kanske fortfarande har skett någon miss någonstans?)

Jan Ragnar skrev:
Tack! Din ritning förtydligar problem och det går ju också utmärkt att sätta a och b yttersterst då det inte förändrar kretsens beteende samt gör det också att kretsen får det standardiserade utseendet hos en tvåpol. Varmt tack!