Sinus grundekvationer, intervall
 Hejsan
Hejsan
jag skulle vilja ha hjälp att se om jag gjort rätt beräkningar.

Hej!
Jag tror du har hittat lösningarna lite utspritt men du har inte riktigt summerat ihop vilka som gäller på intervallet -360<=x<=360. Tänk på att alltid skriva ett tydligt svar.
En grej som blir rätt i slutänden men där du skrivit lite fel är "sinx + 1 = 0 => arcsin(x) + 1 = 0 => x2=-1" (till höger). Du får det rätt sen (dvs -90 + n*360). Tror du tänkte rätt men skrev lite konstigt.
Alltid trevligt att kolla svaren, t.ex. med Geogebra, rita ut vänsterledet (sinx + 1) och högerledet (cosx*cosx), dina lösningar finns där kurvorna skär varandra.
Tänk på att Geogebra räknar i radianer om du inte fixar till det :).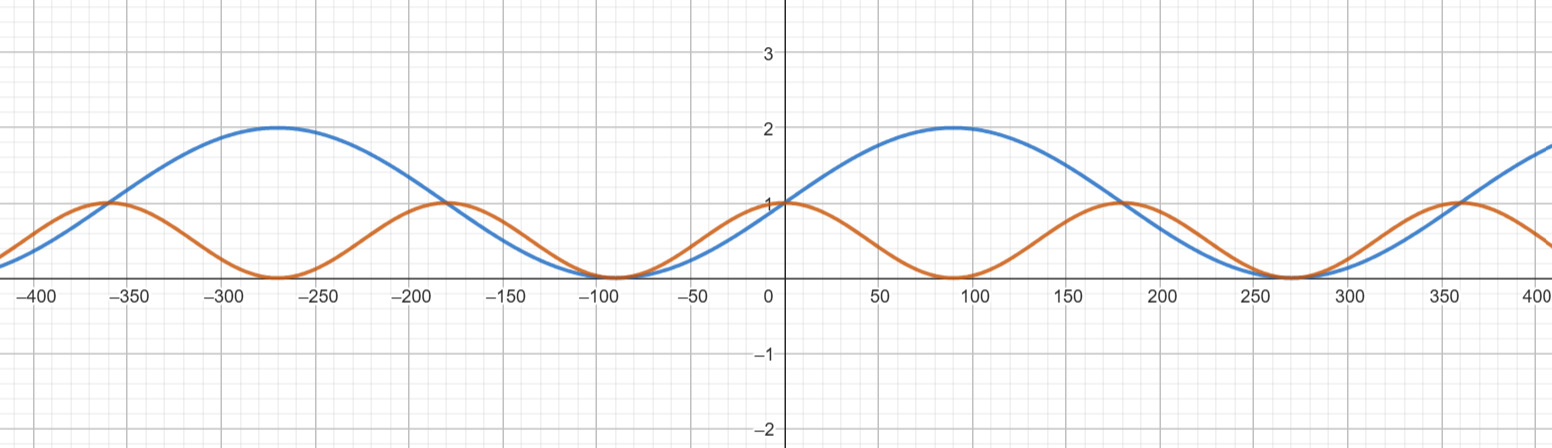
 kan man svara såhär sedan ?
kan man svara såhär sedan ?
PS: menar du att jag istället för att skriva såhär
"sinx + 1 = 0 => arcsin(x) + 1 = 0 => x2=-1" (till höger). Du får det rätt sen (dvs -90 + n*360).
skulle ha skrivit
sinx + 1 = 0 => sinx =-1 => arcsin(x) = arcsin -1 => x2=-1" (till höger).
1) Nah, du skall ju svara vilka lösningar som finns mellan -360 och +360 grader. Med n*360 grader i svaret har du oändligt många lösningar. Jag tycker mig se sex lösningar i figuren.
2) sin x = -1 => x = arcsin(-1) + n * 360 grader => x = -90 grader + n * 360 grader
Ska svaret se ut såhär?
Svar:
i första ekvation sinx=0 : v:n=0, n=1, n=-1
I andra ekvationen sinx=-1 : v : n=0, n=-1, n=1
eller troligen nog:
De fullständiga lösningarna inom intervallet −360≤ x ≤360 är:
x= −360,−180 ,-90, 0 , , 180 , .270, 360. (Grader)
(7 lösningar? 270 grader)
Det du skrev sist. Jag räknade fel, du har rätt med 7 st!


