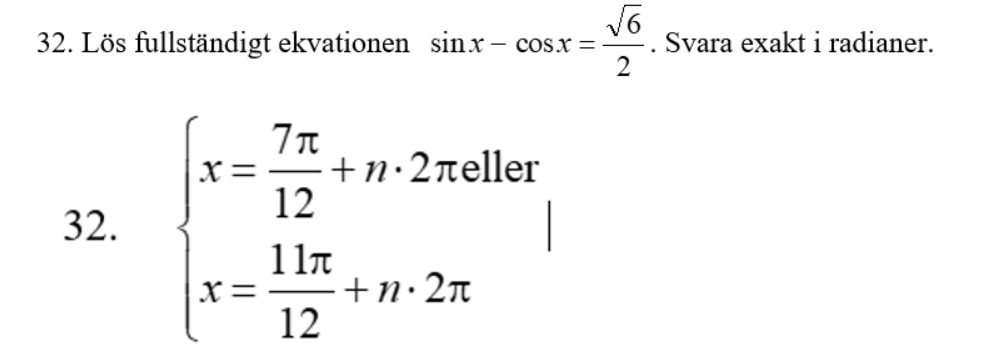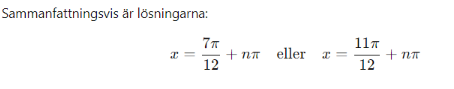sin x-cos x=(√6)/2
Problemet är alltså sin x-cos x=(√6)/2 och ska svaras exakt i radianer (ie inkl perioden.)
Tyvär är min gamla lärare (bild 2) inte kvar på min kurs längre för att kunna påpeka mina tusen slarvfel utan jag får nöja mig med en inspelad genomgång av hur problemet var tänkt att lösas. MEN när jag löser det grafiskt (bild1) är ju perioden 2π (=24π /12) och svaren som anses rätt enligt den inspelade genomgången påstår att bla sin(19π /12)-cos(19π /12)=(√6)/2 när det både enligt grafen och miniräknaren är negativt, -(√6)/2 ! Jag må va trött och virrig men jag brukar kunna fatta vad jag missuppfattat och här gör jag verkligen inte det. Är det för en gångs skull faktiskt inte jag som har fel här?


Det verkar som att du har rätt och att bilden är felaktig. Anledningen till detta är att vid kvadreringen som gjordes så dök "falska rötter upp", notera att om det trigonometriska uttrycket hade varit lika med sqrt(6)/2 så hade inspelningens metod gett som samma lösningar som nu. Man får därför vara noga när man kvadrerar vissa ekvationer om man inte har väldigt bra kännedom, dvs de perioderna som du angav stämmer.
Eagle314 skrev:Det verkar som att du har rätt och att bilden är felaktig. Anledningen till detta är att vid kvadreringen som gjordes så dök "falska rötter upp", notera att om det trigonometriska uttrycket hade varit lika med sqrt(6)/2 så hade inspelningens metod gett som samma lösningar som nu. Man får därför vara noga när man kvadrerar vissa ekvationer om man inte har väldigt bra kännedom, dvs de perioderna som du angav stämmer.
Jaa, det låter vettigt, tack! (Jag skulle aldrig antyda att den läraren inte har god kännedom men man kan inte alltid tänka rätt.)
Jag skulle inte anta att läraren heller har dålig kännedom men alla kan göra misstag (är tyvärr en del av att vara mänsklig).
Det stämmer att kvadrering kan ge fel svar men det gäller vid rotekvationer, inte här. Jag tog uppgiften från mattebanken och deras svar ser ut såhär. Dock utan lösning. Geogebra ger samma lösningar om man räknar ut varje skärningspunkt separat.
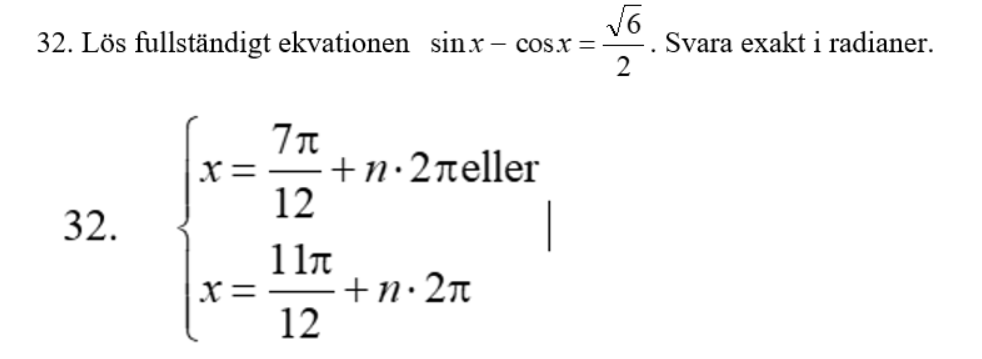
Jag har fråga AI, här kommer svaret:


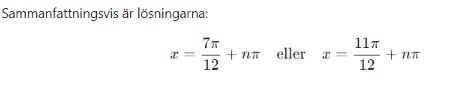
AndJos skrev:Det stämmer att kvadrering kan ge fel svar men det gäller vid rotekvationer, inte här. Jag tog uppgiften från mattebanken och deras svar ser ut såhär. Dock utan lösning. Geogebra ger samma lösningar om man räknar ut varje skärningspunkt separat.
Jag har fråga AI, här kommer svaret:
Men är det inte olika svar här igen? Mattebanken säger +n2π som jag föreslog att det ska vara, medans AIn har löst det som i mitt kursmaterial till +nπ.
Jag och min mattekompis funderade på hur det hur problemet skulle lösas algebraiskt om kvadrering och dubbelvinkelsmetoden blir fel och kollade med chatGPT, här är dens förslag: