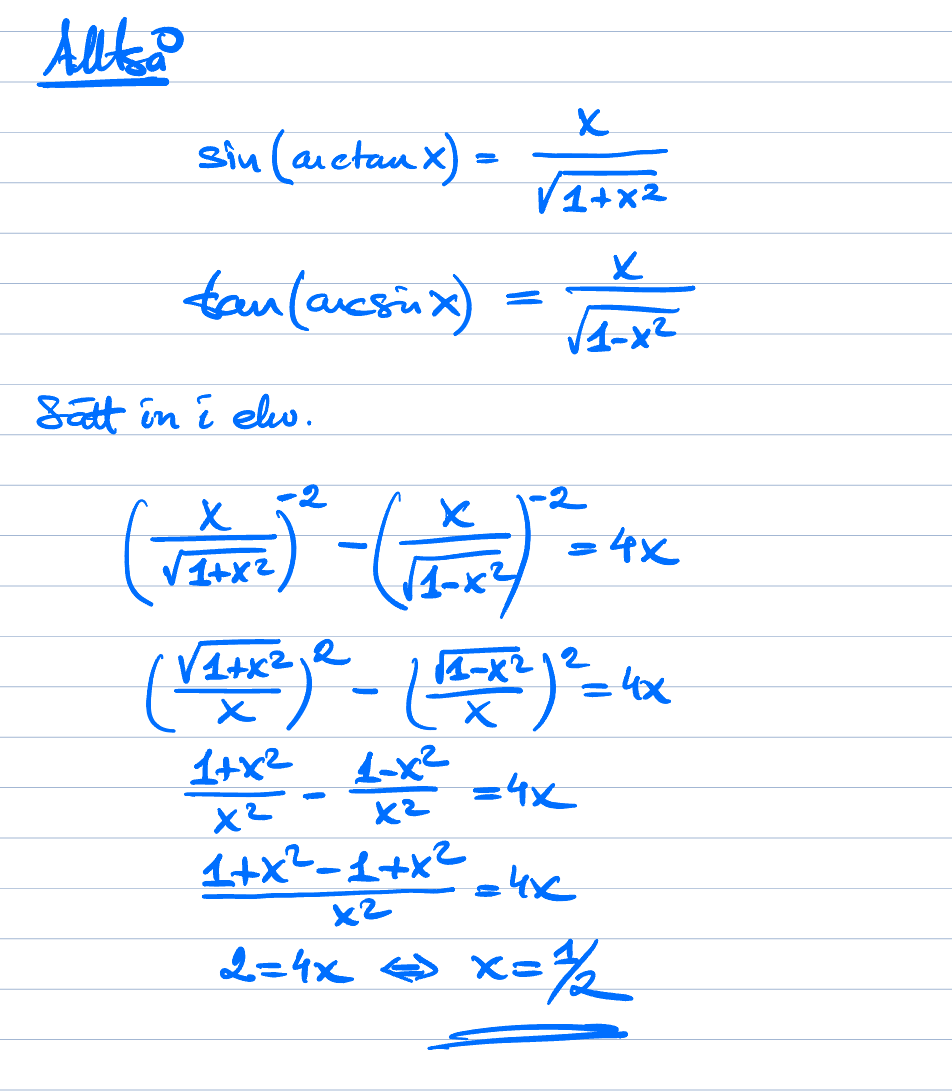sin(arctan(x))

jag fattar inte hur man ska tänka då α tillhör (-π/2, 0]
Är det inte fallet x < 0 som står på femte raden?
Laguna skrev:Är det inte fallet x < 0 som står på femte raden?
Jo men jag hänger inte med i facits resonemang
Vilket steg är oklart?
Laguna skrev:Vilket steg är oklart?
Kan man använda sig utav ett koordinatsystem ( dvs. resonera kring första och fjärde kvadranten, vilket är där arctan är definierad inom bortsätt från -pi/2 och pi/2) för att förklara vad som sker när x < 0? på liknande sätt: 
Jag fattar inte alls hur facit har tänkt...
brunbjörn skrev:Laguna skrev:Vilket steg är oklart?
Kan man använda sig utav ett koordinatsystem ( dvs. resonera kring första och fjärde kvadranten, vilket är där arctan är definierad inom bortsätt från -pi/2 och pi/2) för att förklara vad som sker när x < 0? på liknande sätt:
Jag fattar inte alls hur facit har tänkt...



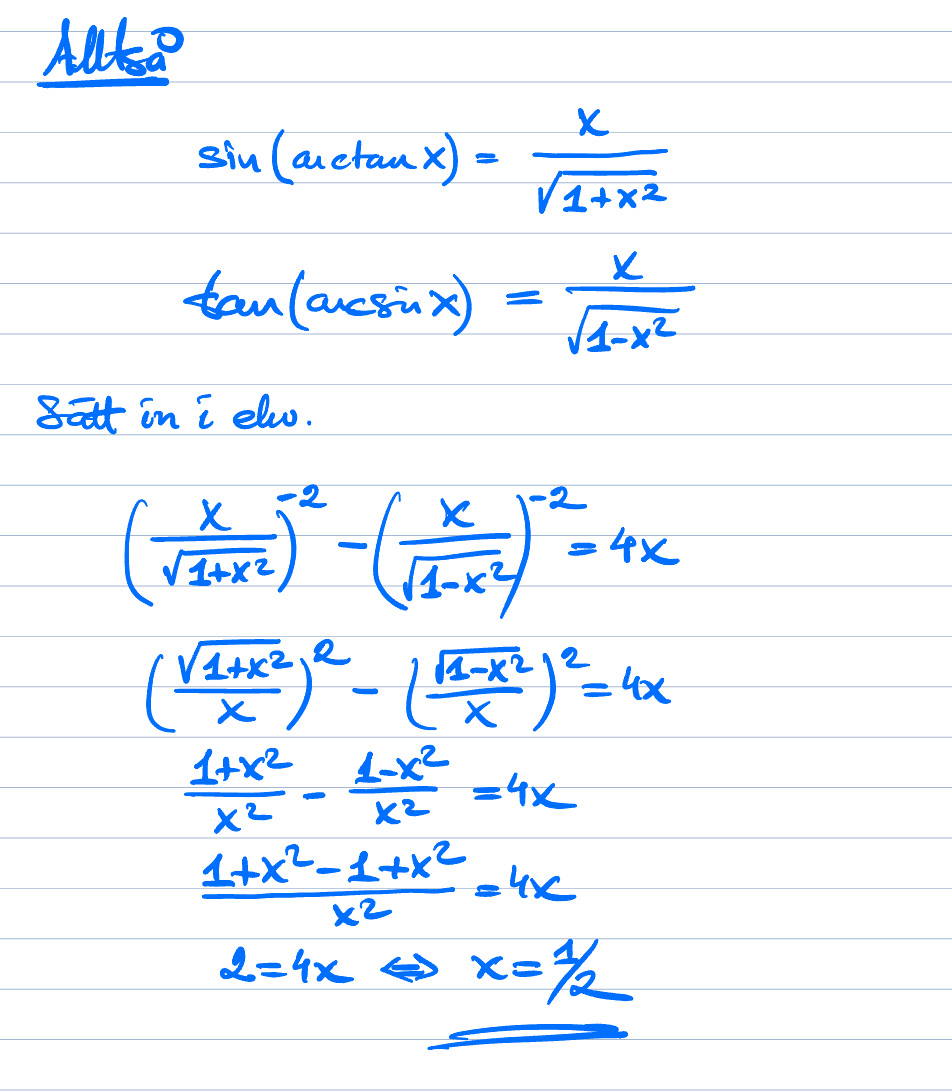
Trinity2 skrev:brunbjörn skrev:Laguna skrev:Vilket steg är oklart?
Kan man använda sig utav ett koordinatsystem ( dvs. resonera kring första och fjärde kvadranten, vilket är där arctan är definierad inom bortsätt från -pi/2 och pi/2) för att förklara vad som sker när x < 0? på liknande sätt:
Jag fattar inte alls hur facit har tänkt...
Tack så jättemycket!!! men jag fattar inte grejen med p... asså det jag inte fattar är varför vill vi att p ska vara positivt? varför tittar vi inte vad som sker då x <0 dvs. att vi föreställer oss att x <0 för då får vi tan(α) = -x /
Vi visar först identiteten för x>0. Sedan antar vi att x är negativ och sätter p=-x, då blir p positiv, och för positiva tal vet vi att identiteten gäller, så då kan vi sätta in p utan problem. Sedan ersätter vi tillbaka till -x och utnyttjar att funktionerna är udda och får att identiteten är densamma, varför den även gäller för negativa tal.