Serier - Divergens, Konvergens eller Absolut konvergens - Envariabelsanalys

jag har fastnat lite på uppgift 2c)
det jag gör är att börja med divergenstestet, vid detta test kommer jag fram till att serien ej är divergent.
För att visa att den kan vara konvergent försöker jag använda mig av jämföresletest men lyckas inget vidare där, jag tänker att serien <=
men jag vet inte riktigt vad jag ska göra sen...
edit: går det ens att göra jämförelsetestet då serien inte endast erhåller värden >0 i intervallet för summan?
För n stort nog är -3n+4 >-0,5n4. Då har vi |(n2+ 2n-1)/(n4-3n+4)|<= <=n2/0,5n4=2/n2 vilket medför att serien är absolutkonvergent.
Tomten skrev:För n stort nog är -3n+4 >-0,5n4. Då har vi |(n2+ 2n-1)/(n4-3n+4)|<= <=n2/0,5n4=2/n2 vilket medför att serien är absolutkonvergent.
vart kommer 0,5n^4 från?
För n stort nog är 3n-4<=0,5n4. Det beror på att vi har potens=1 i VL och potens =4 i HL. Faktor 0,5 tar jag i stället för faktor 1 för att inte döda nämnaren.
Tomten skrev:För n stort nog är 3n-4<=0,5n4. Det beror på att vi har potens=1 i VL och potens =4 i HL. Faktor 0,5 tar jag i stället för faktor 1 för att inte döda nämnaren.
så i nämnaren dominerar n^4 respektive n^2 i täljaren för stora n och således kan serien skrivas om?
Tomten skrev:För n stort nog är 3n-4<=0,5n4. Det beror på att vi har potens=1 i VL och potens =4 i HL. Faktor 0,5 tar jag i stället för faktor 1 för att inte döda nämnaren.
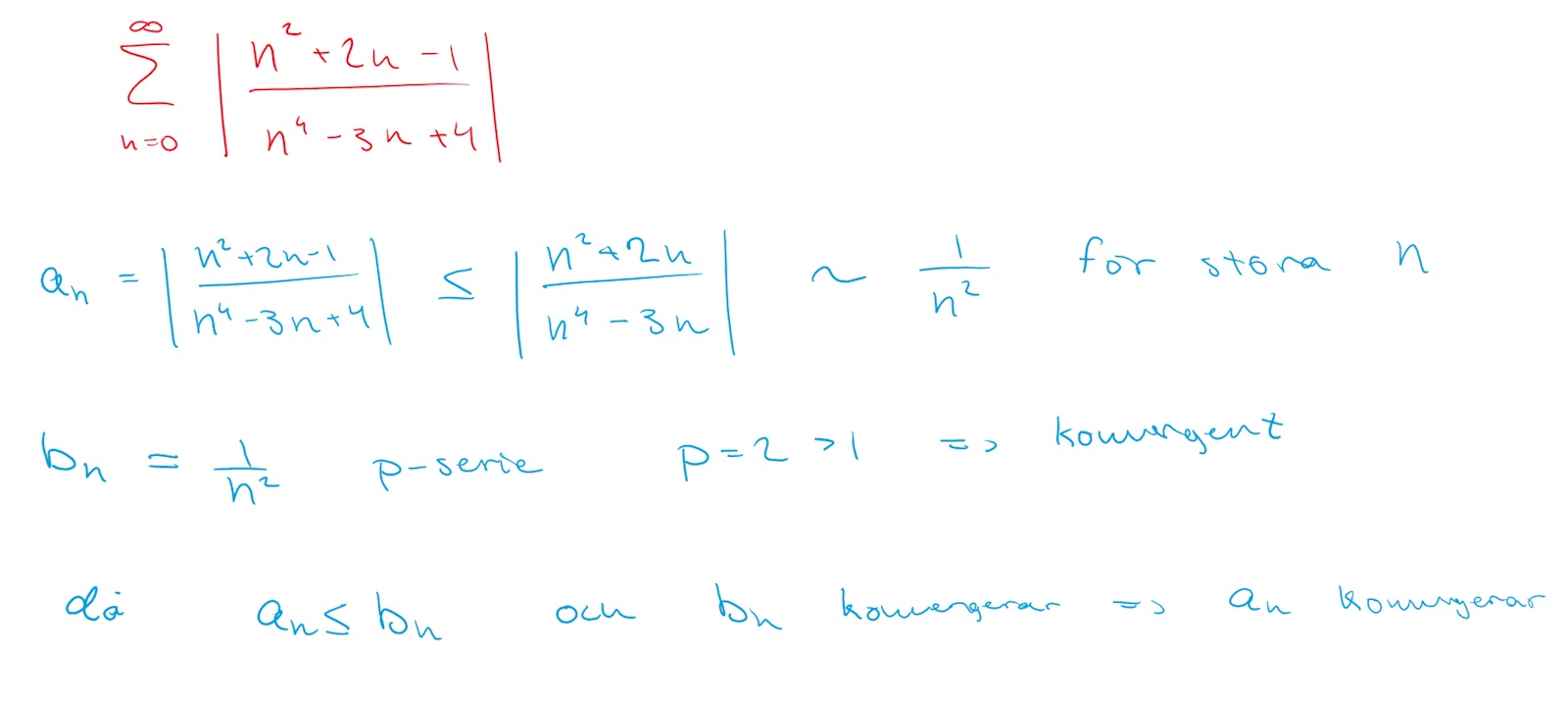
Är detta rätt?
1. Jag tror att jag förstår vad din krumelur framför 1/n2 betyder, men är din lärare med på det?
2. För ordningens skull bör man också visa att nämnaren är skild från 0 för alla n, annars är det ju godnatt för hela serien. För stora n är det redan klart, men den skulle ju kunna hitta på dumheter för små n. I övrigt OK.
Tomten skrev:1. Jag tror att jag förstår vad din krumelur framför 1/n2 betyder, men är din lärare med på det?
2. För ordningens skull bör man också visa att nämnaren är skild från 0 för alla n, annars är det ju godnatt för hela serien. För stora n är det redan klart, men den skulle ju kunna hitta på dumheter för små n. I övrigt OK.
Ja min lärare är med på det, då vi har skrivit så i anteckningarna, "ungefär tecken". Men märker nu att 1/n^2 blir ej def då n=0, vad kan jag göra för att undvika detta? Förstår inte hller hur du gjorde din beräkning tidage :/
Ang 1/n2. Det är här det där med ”för stora n” kommer in + kollen att de verkliga termernas nämnare är skild från 0. Man kan säga att du delar upp summeringen: dels den ändliga summan från 0 tills n blir tillräckligt stor för att uppskattningen ska gälla och dels den oändliga resten av termerna.
Ang hur jag får uppskattningen: Man vet att om vi har termer i form kvoter mellan polynom i n och om nämnarens gradtal är minst lika stor som nämnarens + 2 så har vi konvergens. Sedan är det bara som vanligt att trolla med knäna.
Tomten skrev:Ang 1/n2. Det är här det där med ”för stora n” kommer in + kollen att de verkliga termernas nämnare är skild från 0. Man kan säga att du delar upp summeringen: dels den ändliga summan från 0 tills n blir tillräckligt stor för att uppskattningen ska gälla och dels den oändliga resten av termerna.
Ang hur jag får uppskattningen: Man vet att om vi har termer i form kvoter mellan polynom i n och om nämnarens gradtal är minst lika stor som nämnarens + 2 så har vi konvergens. Sedan är det bara som vanligt att trolla med knäna.
skulle då det svar jag skickade var korrekt eller ej? då för alla n efter 0 så är ju 1/n^2 konvergent enligt p-serie testet, och om den större serien b(n) är konvergent medför det att den mindre serien a(n) också är det?
I den första summan av de ändligt många termer där n är för litet för att uppskattningen ska gälla, så summerar man de VERKLIGA termerna - inte uppskattningens termer. Det är bara i dessa termer som man måste kolla att nämnaren inte är 0. Du summerar inte 1/n2 från 0 till oändl utan bara fr o m det n som är stort nog för att uppskattningen ska gälla.

