Summa av en Serie

$\displaystyle \sum_{n=2}^{\infty} \frac{(-5)^{n}}{8^{2n}}$

Jag försökte med att skriva om den till en geometrisk serie och använda formeln $\frac{a}{1-r}$ men facit gör annat. Kan någon förklara facit?

Edit: Jag tror att de också försöker med samma formel, med jag hänger inte med på stegen :(

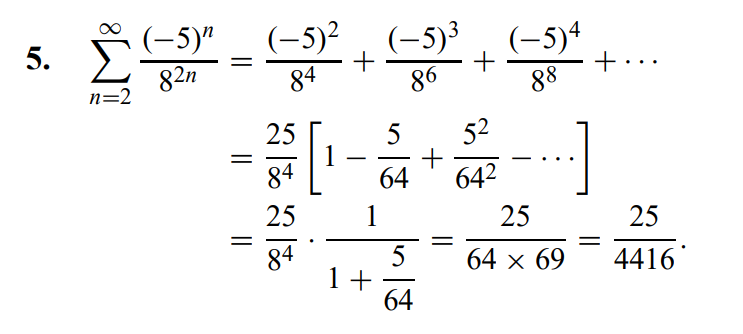
De bryter ut ett gemensam faktor $\frac{25}{8^{4}}$ som finns i alla termer.

Den summan som är inuti [] kan skrivas som följande: $\sum_{n = 2}^{\infty} {(- 1)}^{n - 2} {(\frac{5}{64})}^{n - 2} = \sum_{n = 2}^{\infty} {(- \frac{5}{64})}^{n - 2}$

$\frac{a}{1 - r} = \frac{1}{1 - (- \frac{5}{64})} = \frac{1}{1 + \frac{5}{64}}$

beerger skrev:
De bryter ut ett gemensam faktor $\frac{25}{8^{4}}$ som finns i alla termer.

Jag är helt med på det.

Den summan som är inuti [] kan skrivas som följande: $\sum_{n = 2}^{\infty} {(- 1)}^{n - 2} {(\frac{5}{64})}^{n - 2} = \sum_{n = 2}^{\infty} {(- \frac{5}{64})}^{n - 2}$

Kan man inte istället skriva summan inom [] som en summa $\sum_{n=1}^{\infty} (-\frac{5}{64})^{n-1}$ ??

$\frac{a}{1 - r} = \frac{1}{1 - (- \frac{5}{64})} = \frac{1}{1 + \frac{5}{64}}$

Ok!

Det kan du absolut göra! Även n = 0 och (-5/64)ⁿ mm. konvergerar till samma värde. Var mer för att matcha med startvärdet i ursprungsserien. Smaksak bara! :)

beerger skrev:
Det kan du absolut göra! Även n = 0 och (-5/64)ⁿ mm. konvergerar till samma värde. Var mer för att matcha med startvärdet i ursprungsserien. Smaksak bara! :)

Ok! Då förstår jag konceptet! Tack! :) Kommer nog fler uppgifter snart, I guess :')

Svara

Visa senaste svar