Separabel diffekvation - skum definitionsmängd
Detta är uppgiften:
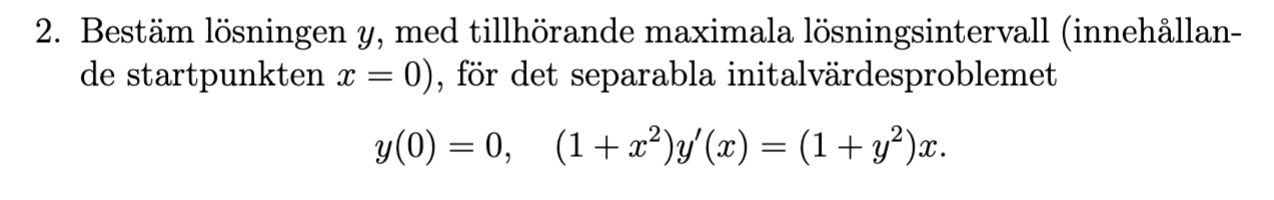
och detta är lösningen (min lärares):
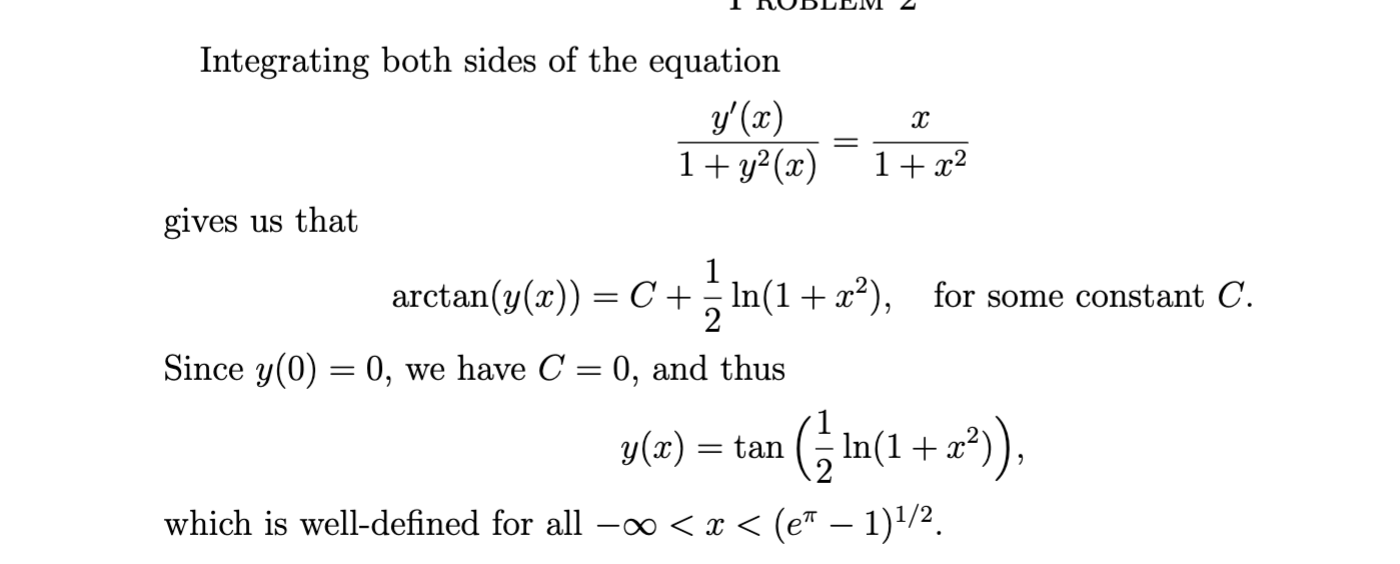
Jag undrar hur det maximala lösningsintervallet blir just så. Jag fick fram att det var definierat för alla x frånskilt där k är något heltal. Mest förvirrande är nog att den är definierad för alla negativa tal.
Jag skulle säga att det är definierat då x är frånskilt . Det de frågade efter i uppgiften var dock det maximala lösningsintervallet som dessutom skulle innefatta att x kunde vara 0. Då blir det som facit säger.
Jag är också tveksam om det verkligen går med k. Vi kommer då ha ln(1+k2*(epi-1)) vilket jag inte tror blir ln(epi) om inte k är 0 och således inte blir att vi tar tangens av pi/2 eller någon annan vinkel på enhetscirkeln som motsvarar division med 0 då vi vill ha tangens.
Vad blir ? Eller vad är det som är väldefinierat?
Bedinsis skrev:Jag skulle säga att det är definierat då x är frånskilt . Det de frågade efter i uppgiften var dock det maximala lösningsintervallet som dessutom skulle innefatta att x kunde vara 0. Då blir det som facit säger.
Hur då?
Jag är också tveksam om det verkligen går med k. Vi kommer då ha ln(1+k2*(epi-1)) vilket jag inte tror blir ln(epi) om inte k är 0 och således inte blir att vi tar tangens av pi/2 eller någon annan vinkel på enhetscirkeln som motsvarar division med 0 då vi vill ha tangens.
Ja, okej. Jag tänkte nog fel med perioden.
D4NIEL skrev:Vad blir ? Eller vad är det som är väldefinierat?
tan(pi/2) som är odefinierat, eller vad menar du? Det är detta som förvirrar mig.
MrPotatohead skrev:Bedinsis skrev:Jag skulle säga att det är definierat då x är frånskilt . Det de frågade efter i uppgiften var dock det maximala lösningsintervallet som dessutom skulle innefatta att x kunde vara 0. Då blir det som facit säger.
Hur då?
Inom matematiken är ett intervall en sammanhängande delmängd av den reella tallinjen eller av en annan partialordnad mängd. Om den enda punkten på tallinjen som inte är gångbar är då x= finns det två möjliga intervall: och . Det senare innefattar inte x=0, så det blir det föregående.
Man skulle också(tror jag) kunna ta ut delmängder ur dessa, t.ex. -10<x<0,005, men de ville ha maximala lösningsintervall.
Hmm, hur är x=-sqrt(e^pi-1) definierat? Eller gångbar?
...bra fråga. Hm.
Med
så är VL till beloppet mindre än π/2. HL måste då har samma begränsning.
Så här ser funktionen ut runt origo. Vill man ha ett intervall som innehåller 0 får man inte ta med tal "på fel sida" av de odefinierade punkterna (eller de odefinierade punkterna själva). Alltså blir funktionen maximalt definierad för
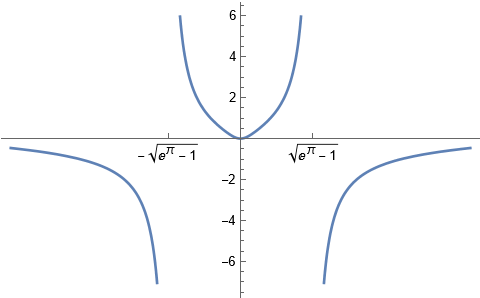
Det var det jag också såg. Blir det något annat när man frågar efter maximalt lösningsintervall? Eller är det helt enkelt fel i facit?
Jag vet inte vad som menas med "maximalt lösningsintervall", har du någon definition?
Med lösningsmängd till en differentialekvation avses ibland mängden av funktioner (lösningar) som uppfyller ekvationen. En funktion måste som bekant innehålla information om såväl definitionsmängd som värdemängd och målmängd. Men här verkar det snarare handla om att maximera ett parameterintervall (en definitionsmängd) som innehåller startpunkten 0 (som därmed uppfyller initialvillkoret) för en given lösning.
Jag tror att det är ett slarvfel i facit.
Har tyvärr ingen definition.
Jag tackar er alla för hjälpen och önskar gott nytt år.



