Sätt att gå, samma?
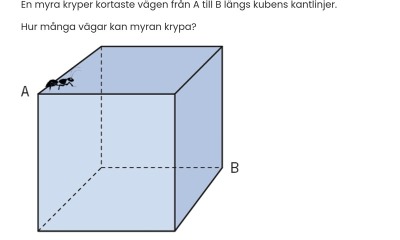
Varför blir lösningen till denna endast 3x2x1 medan denna:

Får lösningen C(10,3)?
Båda har samma strategi, att man räknar hur många steg man kan gå först i de olika "riktningarna" men varför räcker den med myran endast med multiplikationsprincipen medan den med New York handlar det om kombinationen att gå 7steg upp 3 steg åt höger?
Från A kan myran välja tre kanter att krypa längs.
När myran har gjort det hamnar hon i ett nytt hörn.
Från varje sådant hörn skall hon ta sig diagonalt över en kvadrat för att komma till B. Då måste hon välja antingen medurs längs två kanter, eller moturs längs två kanter.
Och i New york uppgiften kan man gå 7 steg upp och 3 steg åt höger och man vill ha antalet sätt, varför kan man inte göra som myran:
7x3?
Vilka sju möjligheter har man i den första korsningen, menar du? Jag hittar bara två: uppåt eller åt höger.
Då förstår jag varför det inte kan bli 7x3.
Men jag fattar inte varför man ska lösa New york frågan med kombinationsformeln?
https://www.pluggakuten.se/trad/manhattan-gator/?#post-b9cf39ac-d3fc-428b-bb69-b120016331f3
Jag förstår inte,
Jag förstår att vi står bland 10 val varav 7 ska vara uppåt och 3 åt höger. Jag förstår även att 10 över 7 och 10 över 3 är samma sak. Men inte varför det blir en kombination.
Har du läst tråden som Trinity2 har givit dig? Här är en länk.
Ja det har jag, men har fortfarande svårt att se det.
Är du med på att för att komma från punkt A till punkt B (utan att gå några omvägar) så behöver man gå 7 steg uppåt och 3 steg åt höger, varken mer eller mindre (och aldrig gå åt vänster eller neråt)?
Ja det är jag
Då skall du gå sammanlagt 10 steg, och 3 av stegen skall vara åt höger, de andra 7 skall vara yppåt. Är du med på detta?
Japp
Man behöver alltså bestämma vilka tre av de tio stegen som skall vara åt höger. På hur många sätt kan man välja vilka tre av de 10 stegen som skall vara åt höger?
Man ska räkna hur många sätt man kan gå den kortaste vägen. Förstår att den kortaste vägen är 3 åt höger 7 uppåt. Men fattar inte varför det blir en kombination.
På hur många sätt kan man välja 3 av 10 är10!/(3!7!).
Ja det förstår jag. Men varför var det ingen kombination på myr uppgiften?
Jag förstår var 10! / (3! 7!) står för. Men inte varför det var en kombination i new york uppgiften och inte också i myr uppgiften?
Uppgifterna är inte så lika som man kanske tror.
Myran och New York-turisten måste tänka på helt olika sätt.
New York: "Tio steg ska jag gå. Varje gång kan jag välja norr eller öster, men jag måste välja tre öster och sju norr av mina tio steg."
Myran: "Först kan jag välja vilken riktning jag vill av tre olika riktningar. Sedan kan jag inte gå tillbaka, så jag måste välja en av två olika riktningar. Därefter finns det bara en riktning kvar (annars blir det mycket längre väg).
Tack!
Vad är det man hade räknat om man tog permutationer på new york uppgiften? Alltså P(10,3)
(Vad P(10,3) kan vara svar på här vet jag inte.)
Uppgifterna är ändå mer lika än en del av oss tyckte. Den mer generella uppgiften är: på hur många sätt kan man gå från (x,y,z) = (0,0,0) till (m,n,k) om man ska öka x eller y eller z med 1 i varje steg.
Myrproblemet ska gå till (1,1,1) och New York-problemet till (7,3,0).
Svaret är .
Inte bekant med den formeln.
Tycker det inte är helt klart än men det blir multiplikationsprincipen i myr uppgiften då man kan gå olika riktiningar på x antal sätt medan den med new york blir en kombination då det är samma väg man ska gå fast att man kan ta 7 steg upp och 3 åt höger i varje kombination.



