Satser och regler i matematik, varför har man de?
Varför har gymnasiematten mer eller mindre blivit = satser, lagar och regler?
Förstår att det finns svåra bevis och att man ibland kan köpa de som de är men tycker ändå att man borde satsa mer på att lära ut och lära sig "bevisen". I alla fall de flesta från gymatte 1 fram t.o.m gymatte 5. Förstår också att det underlättar att inte alltid behöva mecka med bevis. Men man får åtminstone se till att man vet varför satser/regler/lagar fungerar.
Nedan följer ett urval bland många:
- Geometri: Man har 1000 regler känns det som när det mer eller mindre räcker med:
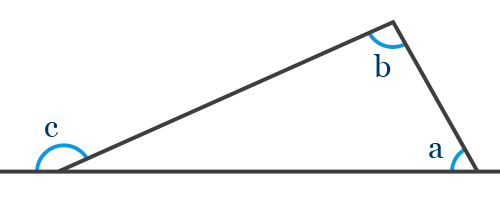
() och .- T.ex. Yttervinkelsatsen: ^C = ^B+A. Behövs formeln?
Enklare är väl att man vet triangelns vinkelsumma och halvcirkelns vinkel
- T.ex. Yttervinkelsatsen: ^C = ^B+A. Behövs formeln?
- Potenslagarna: Vet man varför de funkar så behöver man knappt memorera de.
- . eller
- .
- Algebran: Man lär sig strikt att t.ex. när man har multiplikation så dividerar man och när man har addition så subtraherar man utan att riktigt förstå varför.
- eftersom
- Det man gör på ena sidan gör man på andra eftersom: , adderar man 2 på VL:
. D.v.s man ska addera 2 på HL med ifall man nu vill att likheten ska stämma, ty:
- eftersom
- Parenteslagen eller vad det nu kan heta (när man har minus utanför):
Man lär sig att minus utanför parentesen medför teckenändring och så köper man det och tänker aldrig mer på det. Enklare är väl att se att dvs: .
Nu svamlar jag nog en del men har själv varit i den positionen och lärt mig regel efter regel. Kan rekommendera att stanna upp och tänk efter vad man egentligen håller på med så blir det betydligt enklare. Med Youtube i fickan så kan man nog enkelt söka upp "yttervinkelsatsen bevis" eller vad det nu än är för regel man lärt sig. Notera att jag endast talar om gymnasiematte.
Det är satserna och bevisen som lägger grunden till matematiken. På högre nivåer i matematik pratar man också om axiom, som är lagar kan man säga. Det finns nerskrivet bestämt ett visst antal axiom, exempelvis att 1+1=2. De är väldigt grundläggande.
På gymnasienivå får man bara lära sig räknereglerna rakt av, "så här är den här satsen". In med siffrorna och ut kommer svaret. På universitetet använder du satserna och bevisen till att motivera vad du gör när du räknar. Uppgifterna kan vara så komplicerade att du måste ha satser och bevis för att överhuvudtaget lösa dem.
Matematik är ett språk! Axiom, satser och bevis kan man se som grammatiken, utan dem hade det varit omöjligt att räkna någonting alls!
Hej!
Jag tycker att du väcker en intressant fråga, men att svaren inte är särskilt populära (i den mån de finns).
Det du verkar syfta på är det som kan kallas Riktig Matematik (RM), där man förstår varför saker är på ett visst sätt, istället för att bara lära sig att de är på det sättet. Att undervisa RM kräver lärare som förstår RM, vilket kräver ingående matematikstudier på universitet och högskolor (gärna som forskarstuderande). Väldigt få människor med den kompetensen söker sig till gymnasieskolor, där de förväntas ägna sin tid åt att lära eleverna hur man uppför sig som en civiliserad människa, istället för att ägna sin tid åt matematik.
Ur ett elevperspektiv är det förödande att arbeta med RM eftersom det är krävande, och det är viktigt att elever mår bra och har en stark självkänsla när de lämnar gymnasiet; att arbeta med RM betyder många misstag och motgångar, vilka leder till frustration och låg självkänsla som måste motarbetas till varje pris. Att man lär sig av misstag och motgångar är inte acceptabelt i ett samhälle där känslorna har företräde; tänk om elever känner sig kränkta när de ska läsa Pythagoras sats?
För väldigt många är ren matematik även helt onödigt. Det är en ytterst liten promille i världen som sysslar med just det och behöver känna till alla "detaljer". Man måste komma ihåg varför man går i skolan, syftet är främst för att kunna tillämpa matematiken. Många gånger räcker det då att känna till under vilka omständigheter till exempel ett teorem gäller. Sedan finns möjligeheten, om man vill, att läsa extra eller börja ett rent matematikprogram på universitetet för att utveckla detta.
SVAR TILL: Tomte123:
Axiom är nog ett bättre ord :) Jag håller med dig helt, vid svåra problem så kan t.ex. tabeller och regler vara behändiga. Men tycker att framförallt i gymnasiematten (helt redan vid grundskolematten) borde satsa på att lära sig varför man gör som man gör då slipper man memorera. Håller med att vid tuffa tal i högre nivå så underlättar framtagna recept och klossar. Du lyfter helt klart ett bra argument, men allt borde inte kretsa kring regler och satser m.m. Likt fysiken. Man kommer väldigt långt på väldigt få fysikaliska lagar. Man översätter fysiken till matte. Tyvärr så krånglar man till det i fysiken med en massa formler istället för att satsa på förståelsen.
Har tyvärr gått grund- och gymnasieskolan med att regler och satser är matematik. Fysiken är formler och inget annat. Har ju lite sent förstått att det varit strunt. Allt man gör i gymnasiet har man mer eller mindre berört i grundskolematten. Men man ser ju inte det eftersom man i gymnasiet lär sig "nya" saker. Det "nya" är i själva verket en ny regel/lag ingen ny matematik. Blir riktigt less/irriterad när jag tänker tillbaka på hur lärarna förklarade matte. Blir också arg att jag själv inte förstod bättre och kunde ta tag i det själv i tidig ålder.
Se t.ex. på högskoleprovet. Jämförde det med matten från åk 7, 8 och 9. Det man gör där räcker för att klara hela mattedelen. Men ändå gör man inte det. För man har ju aldrig jobbat med potenslagarna.
Det är nog enkelt för mig o säga detta då jag gjort matten man ska gjort i grund- och gymnasieskolan och på så vis sett "helheten" så långt åtminstone och kan koppla ihop det lite mer. Nåväl nu svamlar jag igen.
Tack för din infallsvinkel. Var rätt bra sagt ändå.
SVAR TILL: Albiki:
Använde lite av det du skrev för ovan svar.
Ja så är det nog. Riktig Matematik (RM) är ett bra ord för det jag beskriver/vill beskriva. RM hade nog varit så mycket bättre för studenter, helst från och med deras första mattekurs då de inte än fått pröva på den enkla (så enkel är det inte) vägen med regler och lagar osv.
Jag tror helt ärligt att om man börjar undervisa RM så kommer det gynna studenterna. Visst till en början är det svårt för det är nog mycket att förstå men sen har man ju olika vägval att välja bland när man löser problem istället för att låsa fast sig på en regel/lag (eller vad det nu kan vara).
Något man borde undervisa är att efter det att man tagit sig igenom det svåra; det som lett till misstagen, motgångarna och lägre självkänslan etc, så blir det hur mycket bättre som helst.
Vet dock inte vem som borde ta tag i det, eleverna eller lärarna. Båda parter kanske. Det känns att RM i lägre matte nivå lär vara enklare än en massa regler/satser/bevis.
Vet inte om det var ett bra svar :) Tycker det du skriver var bra nog för sig självt. Tack för din syn!
SVAR TILL: emmynoether:
Hmm det är faktiskt sant det du säger. Det kan vara onödigt att lära sig alla "detaljer" om man ändå endast ska tillämpa det i begränsade omständigheter. T.ex. något ingenjörsproblem. Då kan regler och teorem komma väl tillhands.
Håller med dig, det beror på vilken riktning man vill ta kanske. Ska man börja i universitetet blir frågan då, kanske. Jag hade faktiskt gärna lärt mig "detaljerna" än reglerna. Hade nog tyckt matten varit roliga då.
Men håller faktiskt med dig, du kommer med en bra infallsvinkel. Tack!
Det skall ju dock nämnas att en del gymnasielärare helt enkelt är riktigt dåliga också, samma gäller fysiklärare. När jag undervisade på Universitetet som extrajobb så försökte jag vara tydlig med matematiska definitioner och reda ut väldigt många förvirringar som elever som kom från gymnasiet hade samtidigt som jag försökte slänga in en del fysikaliska problem som var knutna till den matematiken vi sysslade med. Jag uppfattade det då som att väldigt många gillade att se den fysikaliska biten eftersom den gör att man kan relatera matematiken till någonting "riktigt" ute i världen som man kan ta och känna på.
Det var visserligen blivande ingenjörer jag undervisade för men jag tror nog att de flesta känner mer åt det hållet än att bara sitta och titta på vackra bevis för olika satser. Det brukar bara vara vi som är några få nördar som gillar det :D
sprite111 skrev:SVAR TILL: Albiki:
Använde lite av det du skrev för ovan svar.
Ja så är det nog. Riktig Matematik (RM) är ett bra ord för det jag beskriver/vill beskriva. RM hade nog varit så mycket bättre för studenter, helst från och med deras första mattekurs då de inte än fått pröva på den enkla (så enkel är det inte) vägen med regler och lagar osv.
Jag tror helt ärligt att om man börjar undervisa RM så kommer det gynna studenterna. Visst till en början är det svårt för det är nog mycket att förstå men sen har man ju olika vägval att välja bland när man löser problem istället för att låsa fast sig på en regel/lag (eller vad det nu kan vara).
Något man borde undervisa är att efter det att man tagit sig igenom det svåra; det som lett till misstagen, motgångarna och lägre självkänslan etc, så blir det hur mycket bättre som helst.
Vet dock inte vem som borde ta tag i det, eleverna eller lärarna. Båda parter kanske. Det känns att RM i lägre matte nivå lär vara enklare än en massa regler/satser/bevis.
Vet inte om det var ett bra svar :) Tycker det du skriver var bra nog för sig självt. Tack för din syn!
Jag håller med dig att Riktig Matematik bör undervisas redan i grundskolans årskurs 1; problemet är att det finns studenter på lärarprogrammen som inte kan skilja mellan siffror och tal (allt är siffror för dem), som inte förstår positionssystemet (Varför ställer man upp addition på det sättet?), som inte förstår bråk (Varför är 1/2 samma sak som 3/6?)
Att sätta så svaga människor att undervisa RM till lågstadiebarn är förolämpande, för barnen; det kan mycket väl finnas sjuåringar som förstått att tal är en kombination av siffror och att siffrornas positioner spelar roll.
emmynoether skrev:För väldigt många är ren matematik även helt onödigt. Det är en ytterst liten promille i världen som sysslar med just det och behöver känna till alla "detaljer". Man måste komma ihåg varför man går i skolan, syftet är främst för att kunna tillämpa matematiken. Många gånger räcker det då att känna till under vilka omständigheter till exempel ett teorem gäller. Sedan finns möjligeheten, om man vill, att läsa extra eller börja ett rent matematikprogram på universitetet för att utveckla detta.
Jag skulle vilja säga att syftet med grundskolan i dagens samhälle är att förvara barnen under tiden som deras föräldrar arbetar; om barnen lyckas lära sig någonting överhuvudtaget under förvaringstiden ska detta ses som oväntat och icke-nödvändigt. Att barn presterar dåligt vid alla prov som de utsätts för är inget annat än deras sunda reaktion mot den patriarkala struktur som den traditionella skolan uppenbarligen är.
Även om jag principiellt håller med det mesta i tråden om att matematik bör undervisas med förståelse så är det inte nödvändigtvis så att det är så enkellt eller effektivt som man kan tro. Som våra egna erfarenheter tyder såpå är det ju fullt möjligt att lära sig matematik mekaniskt för att sedan reflektera över dessa förankrade processer och begrepp och transformera sin förståelse över tid.
Att inte tänka kring mening är också ofta nödvändigt för att faktiskt kunna utföra många processer och syftet med satser och regler är ju just att avlasta sinnet och kondensera vad som i praktiken är långa kedjor av kognitiva steg till ett enda.
När du ställer upp potenslagarna genom att stryka faktorer från täljare och nämnare förmodar jag att du använder en regel som du inte nödvändigtvis reflekterar så mycker över och det är okej.
Också har det här RM-begreppet någon förankring i någon viss pedagogisk eller didaktiskt skola? Finns ju massor av skolor där man formulerar en vision om vad god matematikundervisning är men att bara säga riktig matematik är lite för öppet för mig då vi kanske inte är överens om vad riktig matematik är.
Att satser, bevis osv medför att man hinner tugga igenom mer är sant. Frågan man borde besvara kanske är varför gör man matten i skolan? För att man måste? För att bli bra? För att utveckla hjärnan (om man nu gör det med matte, hört att man gör det)? osv...
Men det är nog bra att inte fastna på matten man gör i t.ex. årskurs 8 utan istället få lära sig lite satser/regler och applicera de och successivt bygga upp en förståelse samt reflektera över det man lärt sig i efterhand och utveckla det vidare där. Det kanske är det som är meningen. Att som ovan skrev, ifall man vill fördjupa sig så kan man göra det efter gymnasiet eller då man känner att man har kunskapen till förfogande.
Även vid svårare matte (t.ex. högskole/universitetsmatte) som nämnts ovan är ju satser och lagar som förenklar räkningarna bra att ha, man får nog reflektera i ett senare skede när man har en större bild över det man läst.
Bra infallsvinkel, argument även här ^^
Kommmer att tänka på en fysiker Gerardus t'Hooft som tidigt visade sig ha en stor begåvning för matematik. Toppstudenterna i hans skola lärde sig att använda formler och bevis de blev serverade, men inte t'Hooft. Han föredrog att ta fram sina egna bevis och formler från grunden. Lite jämförbart med att rita och konstruera en bil och därefter bygga den istället för att bara köpa den och använda den. Det här är taget ur boken "Massive The Hunt for the God Parrticle" av Ian Sample och lite fritt översatt av mig.
Vi som inte är födda med t'Hoofts begåvning tycker nog att det är rätt praktiskt med färdiga bevis och formler, men att när man börjat "nosa" på universitetsstudier börjar förstå att det är ett enormt lyft att förstå bakomliggande tankegångar.
Det var väl också det du, sprite111, kom fram till här i slutet på tråden om jag tolkade dig rätt.
Albiki skrev:emmynoether skrev:För väldigt många är ren matematik även helt onödigt. Det är en ytterst liten promille i världen som sysslar med just det och behöver känna till alla "detaljer". Man måste komma ihåg varför man går i skolan, syftet är främst för att kunna tillämpa matematiken. Många gånger räcker det då att känna till under vilka omständigheter till exempel ett teorem gäller. Sedan finns möjligeheten, om man vill, att läsa extra eller börja ett rent matematikprogram på universitetet för att utveckla detta.
Jag skulle vilja säga att syftet med grundskolan i dagens samhälle är att förvara barnen under tiden som deras föräldrar arbetar; om barnen lyckas lära sig någonting överhuvudtaget under förvaringstiden ska detta ses som oväntat och icke-nödvändigt. Att barn presterar dåligt vid alla prov som de utsätts för är inget annat än deras sunda reaktion mot den patriarkala struktur som den traditionella skolan uppenbarligen är.
Jag tycker helt ärligt att ditt lärarförakt är riktigt nonsens. Jag kan bevisa och förstå de flesta satserna i envariabelsanalysen. Jag har läst flervariabels, komplex, linjär algebra, fourieranalys, mekanik, algebra 2, lite topologi, termodynamik, elektromagnetism, energifysik etc.
Menar du seriöst att jag skulle vara så pass outbildad att jag inte kan lära ut vad en enkel liten integral är? Skärp dig. Ditt snack är rent nonsens och visar enligt mig en åsikt som är extremt vinklad från hur du ser världen.
Inlägget redigerat av moderator.
Jag vill påminna om att vårda språket och att vi inte tillåter svordomar i forumet. /Moderator
@woozah
Är du lärare? Är den matematik som du har läst ett krav för att klara av lärarhögskolan?
Det finns fantastiska lärare med stort intresse för de ämnen de undervisar i, men om kunskaperna inte är ett krav finns det heller ingen garanti för att alla lärare kan tillräckligt mycket för att förmedla en djupare förståelse. Man måste nog kunna mer än bara precis det man skall lära ut.
Jag har jobbat med lärare i grundskolan som inte vet skillnaden mellan tal och siffror. Då blir det svårt att undervisa matematik på en djupare nivå (inte högre, bara djupare.) Om sådan undervisning är nödvändig/önskvärd är möjigtvis diskutabelt. Man kommer ganska långt med att bara använda Pythagoras sats eller p/q-formeln utan att förstå hur/varför de fungerar.
Jag har besökt grundskolor där mycket av undervisningstiden gick åt till disciplin och då kanske det inte är läge att gå djupare in på något. Att vara lärare idag är inte så lätt. Jag upplever att de inte får tillräckligt stöd uppifrån, men det finns flera lärare här på PA som kan ge en bättre insyn i detta (i alla fall deras upplevelser).
joculator skrev:@woozah
Är du lärare? Är den matematik som du har läst ett krav för att klara av lärarhögskolan?Det finns fantastiska lärare med stort intresse för de ämnen de undervisar i, men om kunskaperna inte är ett krav finns det heller ingen garanti för att alla lärare kan tillräckligt mycket för att förmedla en djupare förståelse. Man måste nog kunna mer än bara precis det man skall lära ut.
Jag har jobbat med lärare i grundskolan som inte vet skillnaden mellan tal och siffror. Då blir det svårt att undervisa matematik på en djupare nivå (inte högre, bara djupare.) Om sådan undervisning är nödvändig/önskvärd är möjigtvis diskutabelt. Man kommer ganska långt med att bara använda Pythagoras sats eller p/q-formeln utan att förstå hur/varför de fungerar.
Jag har besökt grundskolor där mycket av undervisningstiden gick åt till disciplin och då kanske det inte är läge att gå djupare in på något. Att vara lärare idag är inte så lätt. Jag upplever att de inte får tillräckligt stöd uppifrån, men det finns flera lärare här på PA som kan ge en bättre insyn i detta (i alla fall deras upplevelser).
För att bli en ämneslärare med inriktning mot gymnasieskolan så krävs det att du läst två ämnen, 120 hp samt 90 hp (eller 120+120 om du är svensk- eller samhällslärare). Det är rätt mycket matematik+fysik som ryms i 210 hp, så att låtsas som att ämneslärare är outbildade är givetvis rent nonsens. Ämneslärare är välutbildade inom deras ämnen (och jag kan säga långt överkvalificerade för vad de lär ut!) och det Albiki påstår är ..... (tydligen får man inte skriva det...).
Vad gäller grundskolan så ser jag ännu mindre poäng med att gå in med satser+bevis. Jag tycker progressionen att lära sig räkna (grundskola) och sedan lära sig använda formler+identiteter (gymnasiet) för att sedan djupdyka rakt ner i matematiken är en rimlig ansats. Om man inte heter Albiki då, då vore det kanske bäst att dra upp Peano och bevisa varför 1+1=2 för alla förskoleklasser. Förstår dom inte så det ju inte Albikis problem, för han har troligtvis aldrig rört sig inom skolsystemet.
Kan vi inte bara vara överens om att det finns bra lärare och det finns dåliga lärare precis som att det finns bra läkare och dåliga läkare. Dessutom finns det bra och dåliga arbetsplatser. Jag håller inte med alls om att grundskolan på något sätt handlar om att "förvara barnen under tiden som deras föräldrar arbetar" som albiki skriver, det kan faktiskt vara en av de dummaste sakerna jag hört på länge. Även om utbildningen kan göras bättre på många sätt så lär sig barn otroligt mycket på de 9 år som de går i grundskolan och över 80 % eller så klarar ju målen.
Om du tycker man bör lära ut ren teoretisk matematik i grundskolan som inte ens KTH, Chalmers, etc gör förrän efter man läst envariabel, flervariabel, linjär algebra och gärna någon kurs i differentialekvationer så tror jag snarare det är du som är ute och cyklar lite. Det finns också en anledning till att en sådan kurs endast är obligatorisk om man skall läsa en master i teoretisk matematik men ej en master i tillämpad matematik.
Matematiken skall läras ut som ett verktyg i grundskolan och gymnasiet, ingenting annat. Det viktiga är att lära unga använda matematik, utan att nödvändigtvis bli matematiker. Att bli en duktig matematiker kräver dessutom hundra gånger mer av studenten och mycket mera tid.
emmynoether skrev:Kan vi inte bara vara överens om att det finns bra lärare och det finns dåliga lärare precis som att det finns bra läkare och dåliga läkare.
Jo, givetvis är det så. Men det gäller ju alla yrken så det vore ju konstigt om det inte gällde lärare. Mitt huvudsakliga problem är att många här verkar tro att lärare är inkompetenta. Många gånger har jag hört universitetslektorer som yttrat sig om hur dålig gymnasieverksamheten är när universitet är exakt lika dåliga (eller bra?) på exakt samma sak. Det finns ingen vilja att undersöka hur många som är förvirrade angående det som tas upp i läroplanen och problemet skjuts upp till nästa kurs. Det kan också vara så att man aktivt arbetar för att alla ska bli mindre förvirrade men att enstaka elever ändå håller kvar vid detta synsätt. Det finns så många faktorer i att lära ut att det är väldigt svårt att enbart peka ut "ja just det, läraren var dålig".
Dessutom finns det bra och dåliga arbetsplatser. Jag håller inte med alls om att grundskolan på något sätt handlar om att "förvara barnen under tiden som deras föräldrar arbetar" som albiki skriver, det kan faktiskt vara en av de dummaste sakerna jag hört på länge. Även om utbildningen kan göras bättre på många sätt så lär sig barn otroligt mycket på de 9 år som de går i grundskolan och över 80 % eller så klarar ju målen.
Allt kan bli bättre. Och det arbetas mycket med att det ska bli bättre. Just Albikis uttalande om att skolan är en förvaring får mig att anta att han antingen är själv är förvirrad eller att han har något meta-skämt på gång. Det är helt absurt.
Matematiken skall läras ut som ett verktyg i grundskolan och gymnasiet, ingenting annat. Det viktiga är att lära unga använda matematik, utan att nödvändigtvis bli matematiker. Att bli en duktig matematiker kräver dessutom hundra gånger mer av studenten och mycket mera tid.
Precis. En sats eller ett teorem är inte särskilt användbart när man står på ICA och ska räkna ut hur mycket 50% av 252 gram entrecôte á 279 kr/kg kostar.
NEDAN är svar till ConnyN och under det svar till woozah och allmänt.
ConnyN skrev:Kommmer att tänka på en fysiker Gerardus t'Hooft som tidigt visade sig ha en stor begåvning för matematik. Toppstudenterna i hans skola lärde sig att använda formler och bevis de blev serverade, men inte t'Hooft. Han föredrog att ta fram sina egna bevis och formler från grunden. Lite jämförbart med att rita och konstruera en bil och därefter bygga den istället för att bara köpa den och använda den. Det här är taget ur boken "Massive The Hunt for the God Parrticle" av Ian Sample och lite fritt översatt av mig.
Vi som inte är födda med t'Hoofts begåvning tycker nog att det är rätt praktiskt med färdiga bevis och formler, men att när man börjat "nosa" på universitetsstudier börjar förstå att det är ett enormt lyft att förstå bakomliggande tankegångar.
Det var väl också det du, sprite111, kom fram till här i slutet på tråden om jag tolkade dig rätt.
Ja det var lite där jag landade. Menar absolut inte att man inte ska ta hjälp av alla regler och lagar, och bevis och satser osv. Utan man får ju använda dem men eventuellt försöka reflektera över vad de egentligen är jag gör. Då blir det lite enklare :) De som hjälper på PA behöver inte heller skrota lagar och regler. Det är ju lite det som underlättar när man hjälper andra. Det är väl så som du säger vilket jag instämt med tidigare: man får i efterhand blicka tillbaka och lära sig mer ingående vad det är man gjort.
woozah skrev:
Jag tycker helt ärligt att ditt lärarförakt är riktigt nonsens. Jag kan bevisa och förstå de flesta satserna i envariabelsanalysen. Jag har läst flervariabels, komplex, linjär algebra, fourieranalys, mekanik, algebra 2, lite topologi, termodynamik, elektromagnetism, energifysik etc.
Menar du seriöst att jag skulle vara så pass outbildad att jag inte kan lära ut vad en enkel liten integral är? Skärp dig. Ditt snack är rent nonsens och visar enligt mig en åsikt som är extremt vinklad från hur du ser världen.
Ni båda är oerhört duktiga och smarta, vilket visas varje gång ni hjälper någon här i forumet. Diskussionerna är av olika slag och ni/vi tycker lite olika. Men i grunden vill vi nog alla komma fram till vad som är bäst för de som pluggar och/eller vill lära sig matte. Metoderna får nog anpassas efter syfte och mål.
Kan tillägga att ni båda hade blivit/är bra lärare jag gärna hade haft i tidig ålder. När man är i den nivån ni är i så blir det lätt att man försöker stå upp för sin sak lite mer, kanske.
Alla argument som kommit in för och emot det som diskuteras har varit väldigt insiktsfulla med olika aspekter på ämnet. Men vi får se till att fortsätta vara vänner ty alla har olika åsikter. Dessutom kommer satser, bevis, lagar etc här på PA och i skolan fortfarande att användas (som sig bör) för det är matten helt enkelt, det är så elever lär sig. Att då börja förvilla eleverna kanske inte är passande.
Menar absolut inte att om man lärt sig på det sättet, vilket ändå bör vara ett bra sätt då det funkat (bevis: troligen alla på PA), är mindre kunnig (just p.g.a inflikade bevis intill). Men när man gått igenom grundskolematten, gymnasiematten, eventuellt eftergymnasial-matten så kanske man reflekterar.
- Borde jag gjort något annorlunda?
- Borde någon annan ha gjort något annorlunda?
Jag kom då fram till att man kanske borde lägga tid på fördjupningen. Sedan utvecklades den tanken till att fokus bör läggas på fördjupning för den som vill utan att de som inte vill ska känna sig mindre kunniga (se ovan resonemang). Kanske borde frågan ha varit: ska fördjupningskurser erbjudas för de som vill eller hinner redan i tidig ålder? Men även taken om att man får ta det sen (efter gymnasiet) har slagit mig. Eller kanske skippa det helt då behov eventuellt inte finns. Och det är precis här som meningar går isär. I vart fall mina tankar. Nu eller sen - eller aldrig.
Ni alla bringar fram bra argument och åsikter, och nog kan alla hålla med emmynoether att ren teoretisk matematik är komplicerat och kräver förkunskaper långt över det man lär sig i grundskolan/gy.
Det är inte helt enkelt att säga vad som är rätt eller fel. Den enkla slutsatsen kan man förmodligen inte dra. Och kan väl än en gång nämna att det är viktigt att förstå att "nuvarande" sätt inte är fel. Dock bör man diskutera nuvarande metod för att eventuellt hitta förbättringsområden och eventuella lösningar/förbättringar.Då är det även viktigt att man säger som man tycket och att det är ok.
Tråden bör inte tas som vägledning för huruvida undervisningen ska gå till vare sig i skolan eller på forumet, utan man fortsätter göra som man själv vill göra, kan jag tycka, ty det finns inget rätt/fel.
Man har faktiskt gjort ett försök med "riktig matte" redan på lågstadiet (jag hörde till dem som råkade ut för det). Man baserade all matteundervisning på mängdlära. Forskning och Framsteg hade en artikel om detta.
Precis som smaragdalena säger så finns det forskning på detta. Och forskningen visar att det finns ett svar... Och låt mig tillägga: Svaret är INTE Albikis hittepå.
Dessutom kan lärare inte göra som dom själv vill heller. Lärare ska ju följa den läroplan som finns för de olika ämnena, annars är du inte lärare länge.
Det är ju dock lite tråkigt att det inte finns någon konsensus vare sig här eller i världen om hur man ska undervisa vad som är ganska standardiserat innehåll. Man tycker ju att vi borde ha listat ut det vid det här laget ¯\_(ツ)_/¯
Vi vet ju i alla fall mer om vad som inte fungerar så det är ju bra.
Smaragdalena skrev:Man har faktiskt gjort ett försök med "riktig matte" redan på lågstadiet (jag hörde till dem som råkade ut för det). Man baserade all matteundervisning på mängdlära. Forskning och Framsteg hade en artikel om detta.
Det enda jag minns av det där är nån figur med lång svans som hoppade runt och visade olika mängder.
Smaragdalena skrev:
Man har faktiskt gjort ett försök med "riktig matte" redan på lågstadiet (jag hörde till dem som råkade ut för det). Man baserade all matteundervisning på mängdlära. Forskning och Framsteg hade en artikel om detta.
Väldigt intressant artikel. Den visar om något svårigheten i att besluta hur undervisningen av matematik bör gå till, vilket Serious~ är inne på här ovan.
Ska leta efter någon bok inom serien "Hej Matematik". De borde ju finnas att låna någonstans =)
emmynoether skrev:Kan vi inte bara vara överens om att det finns bra lärare och det finns dåliga lärare precis som att det finns bra läkare och dåliga läkare. Dessutom finns det bra och dåliga arbetsplatser. Jag håller inte med alls om att grundskolan på något sätt handlar om att "förvara barnen under tiden som deras föräldrar arbetar" som albiki skriver, det kan faktiskt vara en av de dummaste sakerna jag hört på länge. Även om utbildningen kan göras bättre på många sätt så lär sig barn otroligt mycket på de 9 år som de går i grundskolan och över 80 % eller så klarar ju målen.
Om du tycker man bör lära ut ren teoretisk matematik i grundskolan som inte ens KTH, Chalmers, etc gör förrän efter man läst envariabel, flervariabel, linjär algebra och gärna någon kurs i differentialekvationer så tror jag snarare det är du som är ute och cyklar lite. Det finns också en anledning till att en sådan kurs endast är obligatorisk om man skall läsa en master i teoretisk matematik men ej en master i tillämpad matematik.Matematiken skall läras ut som ett verktyg i grundskolan och gymnasiet, ingenting annat. Det viktiga är att lära unga använda matematik, utan att nödvändigtvis bli matematiker. Att bli en duktig matematiker kräver dessutom hundra gånger mer av studenten och mycket mera tid.
Håller helt med dig och Woozah.
Det är löjligt och felaktigt att påstå att ”lärarna förväntas ägna sin tid åt att lära eleverna hur man uppför sig som en civiliserad människa, istället för att ägna sin tid åt matematik.”
Ignorant.
Bra svar Emmy


.jpg?width=80&crop=0,0,80,80)







