Satsen om sambandet mellan kontinuitet och deriverbarhet
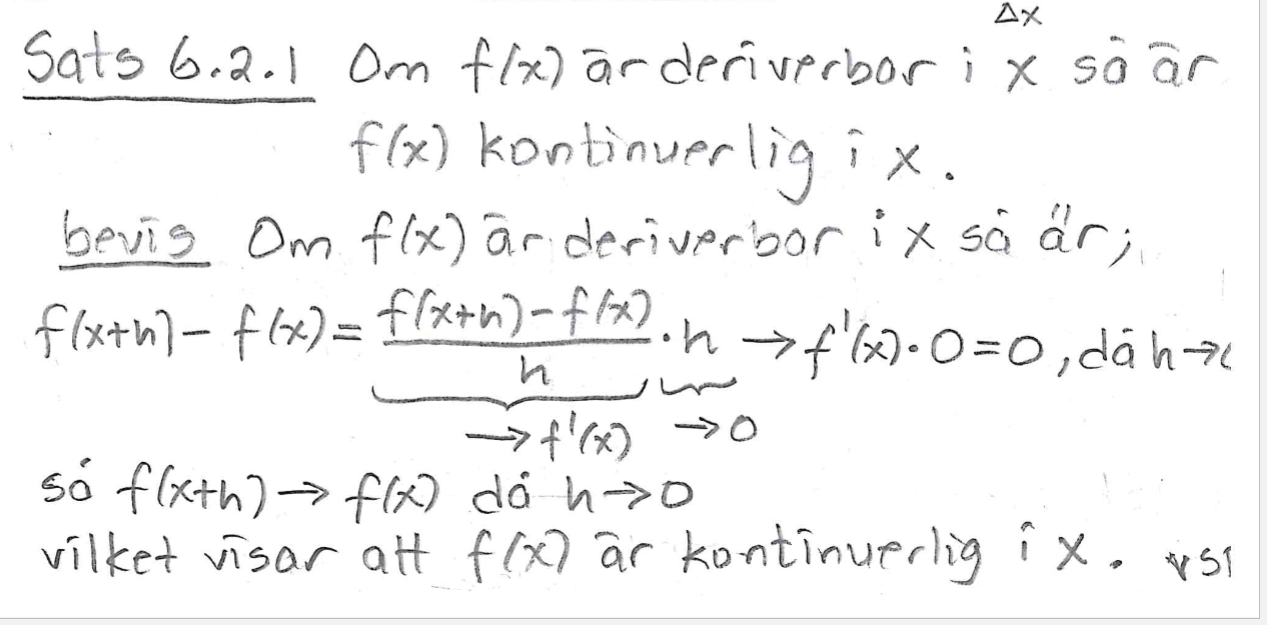
Kan någon förklarar vad det som händer här, jag fattar ingenting.
f är kontinuerlig om f(x+h) = f(x) dvs om ( f(x+h) - f(x) ) = 0.
Sen är man listig och multiplicerar med 1 vilket inte ändrar nåt men man gör det som h/h och simsalabim känner man igen differenskvoten från definitionen av derivata och den har ju ett ändligt gränsvärde eftersom f ska vara deriverbar ...
Sen är man listig och multiplicerar med 1 vilket inte ändrar nåt men man gör det som h/h och simsalabim känner man igen differenskvoten från definitionen av derivata och den har ju ett ändligt gränsvärde eftersom f ska vara deriverbar ...
Jag förstår inte din kommentar! Pratar tydligare.
f(x+h) - f(x) = (f(x+h) - f(x))1 = (1 = h/h) = (f(x+h) - f(x)) = .
PATENTERAMERA skrev:f(x+h) - f(x) = (f(x+h) - f(x))1 = (1 = h/h) = (f(x+h) - f(x)) = .
Men vi behöver inte göra så här. Känns onödigt.
Du sa ju att du inte fattade. Nu säger du att förklaring är överflödig. Hur skall du ha det?
Jag sa ja inte fattade för att matsC förklarar nå om multi. med 1 och "simsalabim"? Ja förstår inte vad han menade och därför be ja honom att pratar tydligare.
Jag visade bara mer matematiskt det som MatsC beskrev med ord. Fattade du gången?
PATENTERAMERA skrev:Du sa ju att du inte fattade. Nu säger du att förklaring är överflödig. Hur skall du ha det?
Jag menar inte orespekt.
PATENTERAMERA skrev:Jag visade bara mer matematiskt det som MatsC beskrev med ord. Fattade du gången?
Ja, ja tror så.
Så det som ja förstår tills nu är att beviset handlar om att visar f(x+h) går emot f(x) när h går emot 0, varför visar det att f(x) är kontinuerligt i x. Hänger ja fortfarande inte med.
På gymnasiet brukar man per definition säga att en funktion f är kontinuerlig i x om
.
Detta är ekvivalent med
.
Ja. är ekvivalent med .



