Sannolikhetsteori. Diskontinuerlig CDF till PDF.

Behöver lite hjälp med (c)-uppgiften. Planen är att först hitta pdfn fL(l) och jag försöker följa boken där de börjar med att uttrycka cdfn FL(l) mha Heaviside-funktionen, för att till slut få pdfn. Enligt facit så är cdf respektive pdf nedan.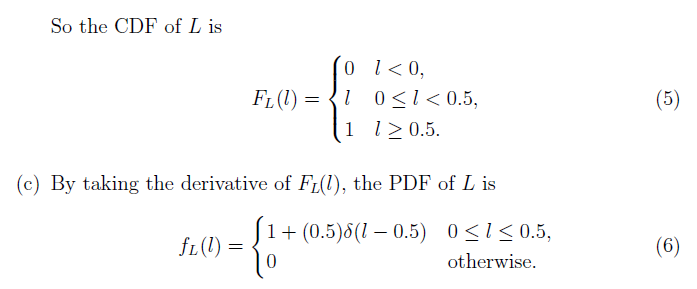 Nu visar de inte hur man uttrycker cdfn mha Heaviside-funktionen, men jag antar att detta är det första vi ska göra. Jag får cdfn till FL(l)=lu(l)-lu(l-0.5)+u(l-0.5). När jag sedan ska uttrycka pdfn dyker jag på lite problem, jag har en summa av produkter, i boken visar de endast exempel med konstanter. Se detta exempel nedan
Nu visar de inte hur man uttrycker cdfn mha Heaviside-funktionen, men jag antar att detta är det första vi ska göra. Jag får cdfn till FL(l)=lu(l)-lu(l-0.5)+u(l-0.5). När jag sedan ska uttrycka pdfn dyker jag på lite problem, jag har en summa av produkter, i boken visar de endast exempel med konstanter. Se detta exempel nedan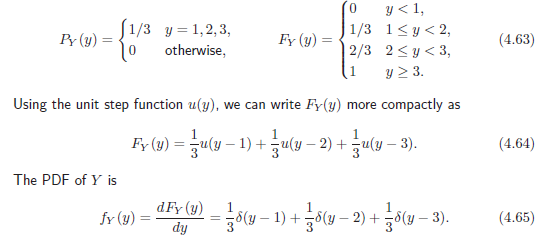
Hur gör jag i mitt fall? detta är lite oklart. Derivatan av en Heaviside är Dirac's delta-funktion, jag vet inte riktigt hur de gör.
Din funktion är inte disjontinuerlig, så du får inga Dirac-funktioner.
Laguna skrev:Din funktion är inte disjontinuerlig, så du får inga Dirac-funktioner.
FL(l) är diskontinuerlig vid l=0.5
Sant.
Ska E(L) vara medelvärdet av L ?
I så fall: L är summan av två delar med vardera sannolikheten en halv och med lätt fastställbara medelvärden.
farfarMats skrev:Sant.
Ska E(L) vara medelvärdet av L ?
I så fall: L är summan av två delar med vardera sannolikheten en halv och med lätt fastställbara medelvärden.
E[L] är medelvärdet, ja.
Jag tror att man måste visa hur man kommer fram till svaret matematiskt.
If You say so. Good luck on the heavy side :)
farfarMats skrev:If You say so. Good luck on the heavy side :)
Tack, det lär behövas!
Vet ej om cdf:n är korrekt, men låt säga att den är det. Att den är en summa av produkter ändrar inte metoden direkt, pdf:n är fortfarande derivatan av cdf:n, så det är bara derivera som du skulle deriverat i vanliga fall. Du får bara komma ihåg produktregeln för derivator, att (fg)’ = f’g + fg’
Men en spontant tanke. Du vet att V ~ Uniform(-1, 1). Och du vet att L = f(V). Om du då ska räkna ut E[L], kan du inte använda att
E[f(V)]=∫∞-∞f(V)p(V)dV, där p(V) är pdf:n för V?
Hondel skrev:Men en spontant tanke. Du vet att V ~ Uniform(-1, 1). Och du vet att L = f(V). Om du då ska räkna ut E[L], kan du inte använda att
E[f(V)]=∫∞-∞f(V)p(V)dV, där p(V) är pdf:n för V?
Jag tror att E[L]=int l f_L(l) dl. Dvs vi måste hitta ett uttryck för pdfen till L
Cien skrev:Hondel skrev:Men en spontant tanke. Du vet att V ~ Uniform(-1, 1). Och du vet att L = f(V). Om du då ska räkna ut E[L], kan du inte använda att
E[f(V)]=∫∞-∞f(V)p(V)dV, där p(V) är pdf:n för V?
Jag tror att E[L]=int l f_L(l) dl. Dvs vi måste hitta ett uttryck för pdfen till L
Ja det är väl ett sätt, men låt säga att L = V^2, och du vill räkna ut E[L] = E[V^2]. Då hade du väl inte börjat räkna ut pdf:n för V^2? Du hade väl bara räknat ut int v^2f_V(v)dv?
Jag provade att räkna med denna metod och kanske att jag gick bort mig i integralerna, men kan 3/8 stämma tro?
Okej jag såg nu att du hade ett facit som faktiskt löste uppgiften med hjälp av b) (och inte bara ett exempel från tidigare), så jag kanske är ute och cyklar här
Inser nu också att de då skrivit ut pdf till L och då får jag E[L] = 0.375 = 3/8? I sådana fall verkar ju min föreslagna metod funka, även om jag inser att iom att b-uppgiften är vad den är kanske provskaparen tänkte/hoppades att man skulle använda den metod som står i facit
Hondel skrev:Inser nu också att de då skrivit ut pdf till L och då får jag E[L] = 0.375 = 3/8? I sådana fall verkar ju min föreslagna metod funka, även om jag inser att iom att b-uppgiften är vad den är kanske provskaparen tänkte/hoppades att man skulle använda den metod som står i facit
Ja det ska stämma att E[L]=0.375.
Jag kom fram till att följande metod var enklast för mig (slipper Heaviside).
Plotta FL(l)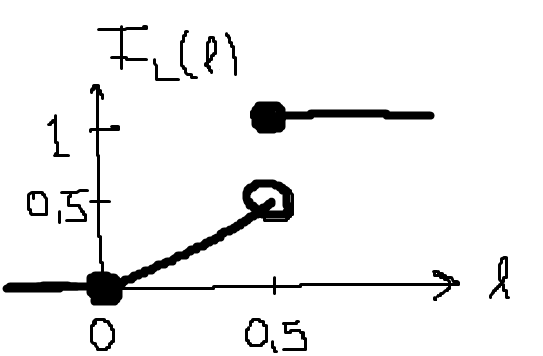
PDFn är derivatan av CDFn. De linjer med konstanta värden är derivatan (lutningen) 0, dvs för l<0 och l>=0.5. Så vad vi egentligen bör göra är att vara uppmärksamma där vi har diskontinuitet, vid l=0.5, här är derivatan Dirac-funktionen (förskjuten), annars deriverar vi som vanligt.
så fL(l)=d/dl FL(l)=d/dl l + l(0.5)delta(l-0.5)=1+0.5delta(l-0.5) för 0<=l<=0.5 och 0 annars. Sen är E[L] ganska straight forward.
Tack för hjälpen för övrigt!
Alright, ja vad som funkar för dig är det viktigaste. Men kanske ändå bra att komma ihåg att E[g(X)]=∫∞-∞g(x)fX(x)dx gäller generellt


