Sannolikhet för att behöva köpa ett visst antal för att få ett exakt annat värde
Min fråga lyder: "I ett mycket stort lotteri ger i genomsnitt var fjärde lott vinst. En person bestämmer sig för att köpa lotter tills han vunnit exakt två gånger. Vad är sannolikheten att han måste köpa exakt fem lotter?
Jag tänkte först att det var en geometrisk fördelning, men kom ingen vart. Sen gick jag i tankarna på en binomial fördelning och tänkte att jag kanske kunde räkna ut chansen att vinna en lott på de fyra första, men sedan har jag ingen aning hur jag skulle kunna göra sen.
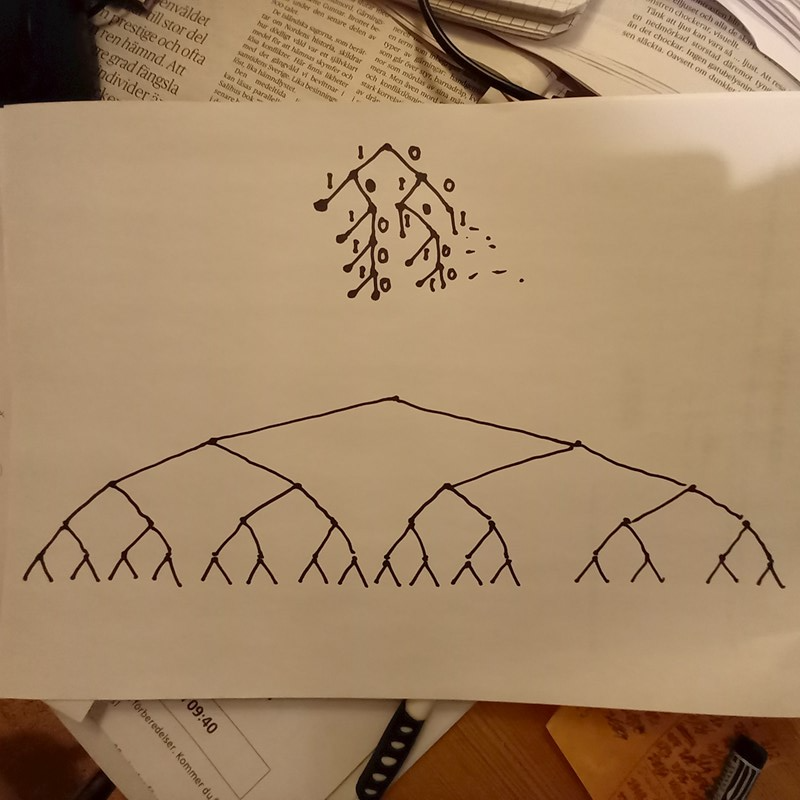
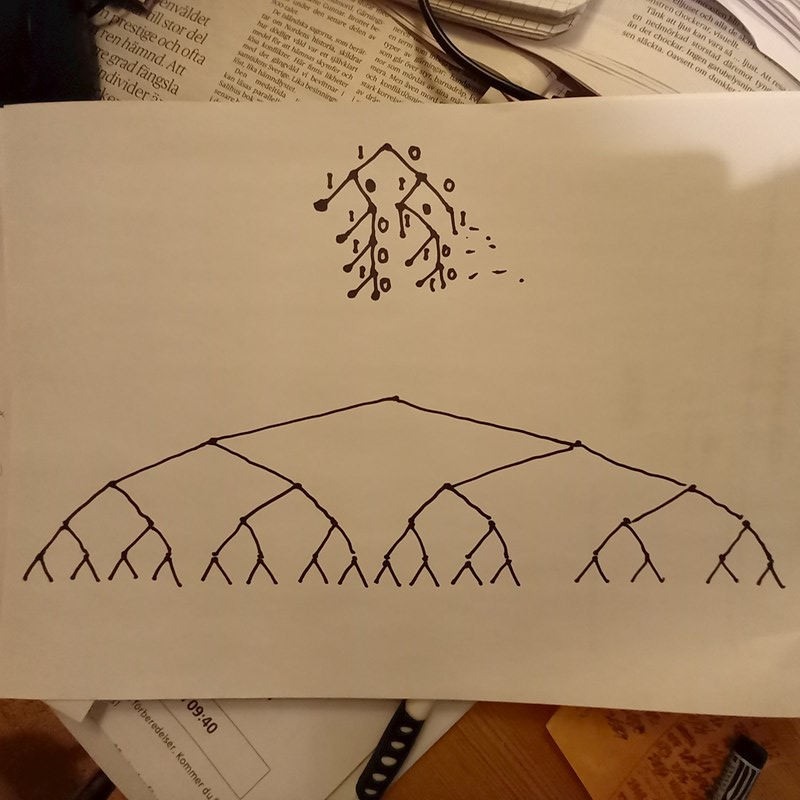
Jag skulle rita ett träddiagram.
Laguna skrev:Jag skulle rita ett träddiagram.
Jag verkar ha omöjligt för att rita ett träddiagram. Lyckas till typ försök 2 sen så överlappar alla linjer varandra och det går inte att se vad som står :/
Mm.
Det övre blev inte snyggt på första försöket, men jag försökte utnyttja att man kan sluta när man har två vinster (1:or).
Nu tror jag vi har bildbuggen här igen. Jag lade in en bild och bytte sen ut den mot en bättre bild, men nu syns ingen bild här längre. Den syns på min mobil.
Vad gäller för de första fyra lotterna?
Bubo skrev:Vad gäller för de första fyra lotterna?
Det är väl att chansen att vinna är 0.25. Försökte med ett träddiagram och multiplicerade 2 vinster med 3 förluster(3/4) men det gav inte rätt svar, så jag har verkligen ingen aning vad jag ska göra
Laguna skrev:
Tack! Förstår dock inte hur jag kan använda ett träddiagram för att lösa min uppgift. Försökte multiplicera chansen att vinna(1/4) två gånger, och sedan det med chansen att förlora 3 gånger(3/4) men fick inte rätt svar
Markera alla lyckade utfall i diagrammet. Beräkna sannolikheten för varje. Addera.
Din metod fungerar nog om man alltid köper fem lotter, men man slutar ju när man har två vinster. Du behöver ändå multiplicera med antalet sätt att få två vinster och tre förluster.
Laguna skrev:Markera alla lyckade utfall i diagrammet. Beräkna sannolikheten för varje. Addera.
Din metod fungerar nog om man alltid köper fem lotter, men man slutar ju när man har två vinster. Du behöver ändå multiplicera med antalet sätt att få två vinster och tre förluster.
Super! Nu har jag förstått. Matematik och jag kommer inte alltid överens, men tycker att det är superkul att fundera över problem och komma till lösningar även om det tar ett tag och hjälp krävs. Tack så mycket :)
Den femte lotten är vinst, annars hade man inte köpt den.
De fyra första lotterna måste då vara en vinstlott och tre nitlotter i ordning VNNN, NVNN, NNVN eller NNNV.