Samma fråga men olika lösningar?

Hodlys skrev:

Hej!

Jag stötte på de här två frågorna som liknar varandra men som löses på olika sätt. Det är inte heller så att jag kan använda samma lösningsmetod på båda frågorna, vilket jag tycker är ganska konstigt. Därför under jag varför de löses annorlunda?

 

Fråga 1 med lösning (fokusera på b) ):

 

 

 

fråga 2 med lösning (fokusera på a) ):

Kan det också vara så att i första frågan finns det inte en konstant framför sin/cos medan i andra frågan finns det en sådan konstant?

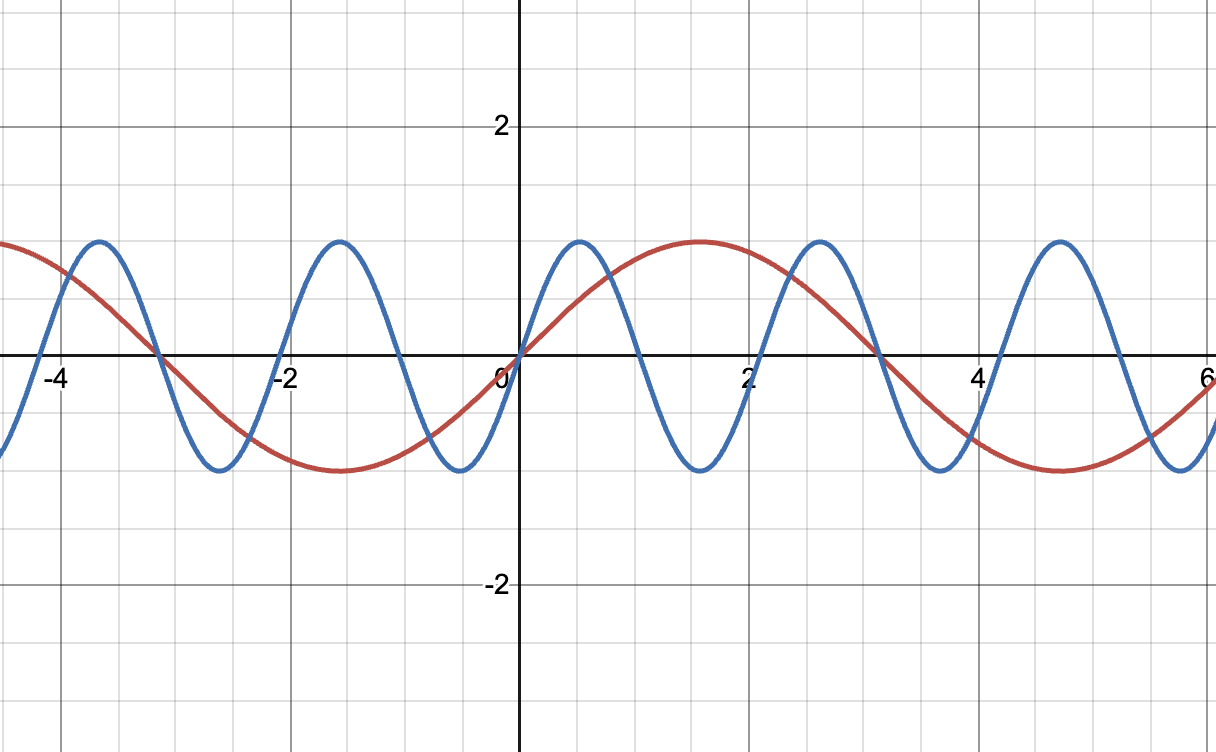
Sinuskurvor kan skrivas allmänt på formen: y=Asin(k*x)+d

I första uppgiften är A och d lika i båda kurvor. Bara är olika. Grafiskt ser detta ut enligt följande: 

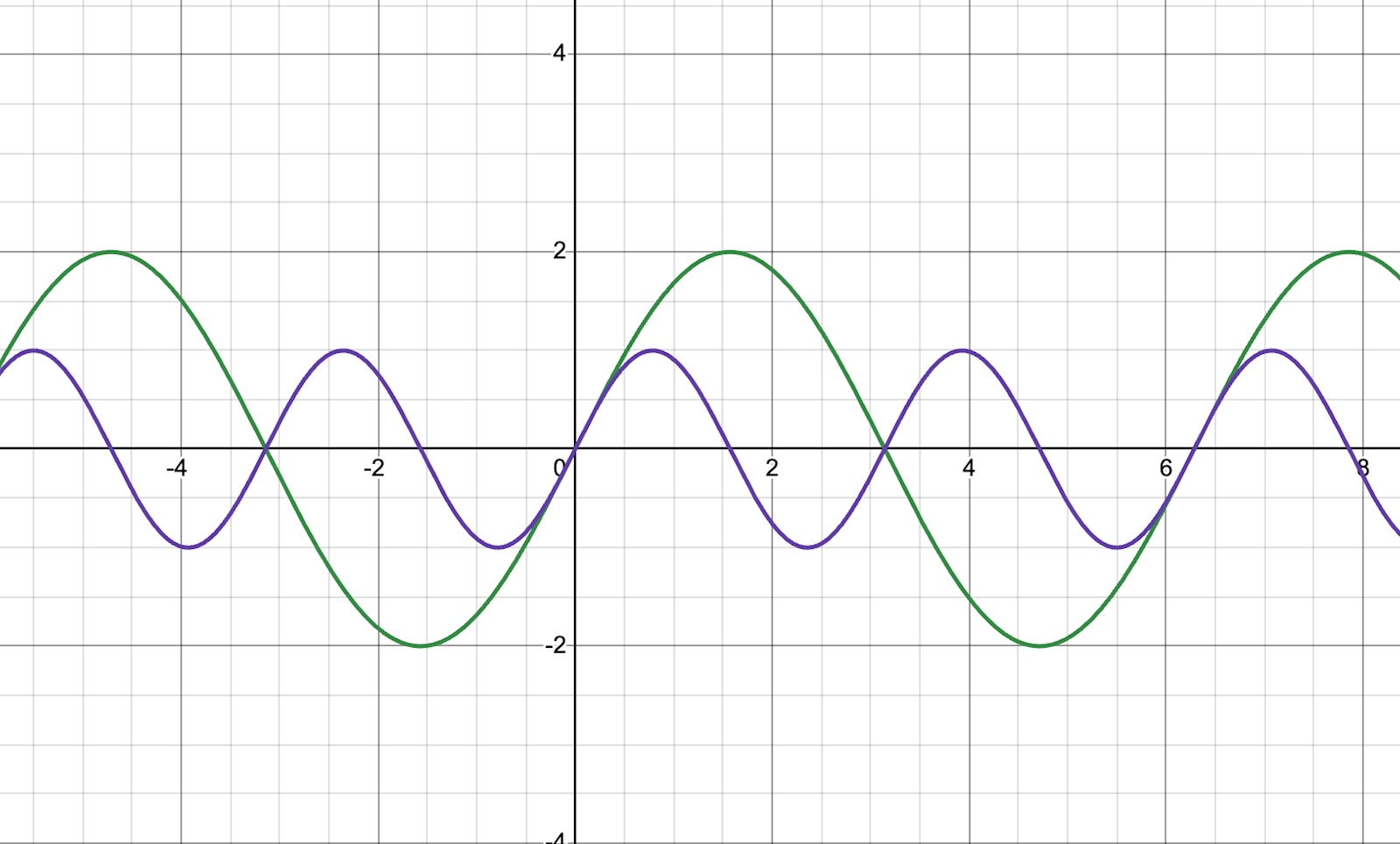
I andra uppgiften är det istället A och k som är olika. Detta gör det egentligen svårare men just här gick det lätt med formeln för dubbla vinkeln: 

Så det du skrev ovan stämmer. Det är att amplituden också skiljer som gör uppgifterna annorlunda. 

Mrpotatohead skrev:

Sinuskurvor kan skrivas allmänt på formen: y=Asin(k*x)+d

I första uppgiften är A och d lika i båda kurvor. Bara är olika. Grafiskt ser detta ut enligt följande: 

I andra uppgiften är det istället A och k som är olika. Detta gör det egentligen svårare men just här gick det lätt med formeln för dubbla vinkeln: 

---

Så det du skrev ovan stämmer. Det är att amplituden också skiljer som gör uppgifterna annorlunda. 

så om jag möter en likadan uppgift som i fråga 1 så kan jag bara jämföra vinklarna medan om jag möter en uppgift som fråga 2 bör jag använda mig av andra metoder (som faktorisering osv)?

Ja, precis. Att lösa ekvationer av formen: sin(u)=sin(v) med metoden i första frågan är en standardmetod, dvs att sätta: 

$u=v+n*360$ eller $u=v+n*2\pi$

I den andra får man ta det lite som det kommer. Det beror på uppgift:)