Rullvillkor - tecken
Hur får dom att bli negativt? Jag är med på hela lösningen förutom den delen.
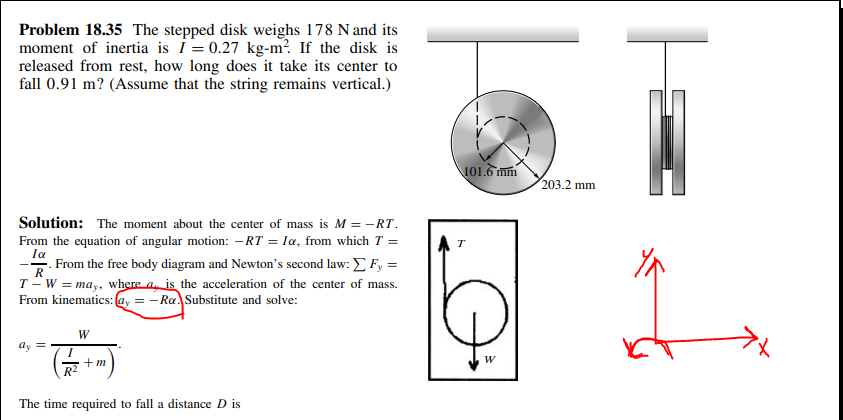
Det verkar som de har tänkt sig y-axeln neråt och moturs som positiv rotationsriktning.
Notera att med y-axeln uppåt blir svaret tossigt, eftersom det skulle innebära att accelertionen var uppåt eftersom de anger ett positivt värde på ay.
Tillägg: 9 mar 2022 15:05
Hm, deras svar går inte ihop riktgt.
Det borde nog vara som du säger att ay = R.
När de skriver T - W = may så är det klart att de tänker sig y-axeln riktad uppåt.
När de skriver -RT = I så är det klart att de tänker sig moturs som positiv riktning eftersom momentet uppenbart är medurs. Notera att detta innebär att är ett negativt värde.
Så vi borde ha att ay = R. ay blir då negativt, som sig bör, då är negativt.
Ja exakt, försökte också att se problemet från andra referenssystem men då fick jag teckenfel på andra ställen. Jag vet ju hur man beräknar kryssprodukten osv.
Hur du nåt tips så jag inte gör fel på tentan när det kommer till just om man utgår från referenssystemet i bilden? Visst är densamma som används till friktionskraften? och är positiv moturs?
Vilken friktionskraft? Det finns väl ingen friktionskraft i detta problem.
Ops, menar istället för friktionskraften.
OK. Ja, det är samma R, dvs den lilla radien i figuren.
Som sagt, om vi väljer y-axel uppåt och moturs som positiv rotation, så är både ay och negativa, dvs mindre än noll.
Rätt svar är då
R = ay = .



