Rotationsvolymer, x eller y
hur ska man tänka när man väljer med avseende på x eller y

i den här uppgiften tillexempel så tänkte jag att eftersom radien berodde på y så borde formen för volymen skrivas om till:
vilket då ger att volymen blir:
hur ska man tänka?
Strategin, som du verkar ha varit inne på själv, går ut på att skapa oändligt många, "infinitesimalt tunna" diskar och sedan summera alla mellan ändpunkterna. Om vi föreställer oss en sådan disk (och väljer en icke-infinitesimal bredd) skulle den ha följande volym:
, där motsvarar hur bred vi låter en disk vara (fortfarande ett litet tal).
Om vi nu låter får vi följande volym på ett sådant disksegment:
Nu summerar vi upp alla dessa volymelement från 0 till 2 och får då:
Just nu så förstår jag ej din förklaring hehe, kan ha och göra med att jag är trött också men det jag var ute efter är typ vad är det som bestämmer att du ska göra om ekvationen låt oss säga att vi har kurvan:
vi ska ta fram en rotationsvolym mellan kurvan och x axeln när den roterar runt y-axeln
varför väljer jag att skriva det som
och inte
är det efter den axeln som kurvan roterar runt som bestämmer det eller är det liksom eftersom vi använder oss av skivor med höjden oendligt små hopp i avseende på x led. Förstår du mig haha?
edit: alltså när vi tar fram själva radien för cirkelskivorna
Våra volymelement befinner sig ju längs x-axeln, så det är väl logiskt att man då också summerar längs x-axeln?
EDIT: oj, nu ser jag att du skrev runt y-axeln! Ja då är det ju såklart en annan femma. Men i ursprungsuppgiften skedde ju rotationen kring x-axeln.

Om man struntar i vad kurvorna faktiskt betyder är det unge fär såhär man ska tänka?
Alltså så här:
Om din kurva roterar kring y-axeln, då motsvarar gränserna i integralen y-värden och då får man dessutom ett istället för ett i slutet enligt samma logik som ovan.
Okej eftersom det står i varenda uppgift vilken axel den roterar kring så är det bara att utgå efter det som står i uppgiften står det att den roteras kring y så gör jag om den så att ekvationen är skriven i x = sqrt(y) och använder sedan gränserna i y led och och om den roterar kring x axeln så använder jag ekvationen som den är skriven och har gränser i x?
Ja, det låter rätt. Men jag tror det är bättre att försöka förstå själva metoden istället för att försöka komma ihåg någon regel (även om den stämmer).
Ja men tror jag förstår metoden, det ända var det där eftersom jag inte när och hur jag ska skriva om ekvationen det är allt
Det är mest det som gör mig osäker på mina svar i uppgifterna, liksom har jag beräknat rätt volym nu
Metoden är att kurvan delas upp i skivor med med en höjd som går mot noll sedan beräknas summan av dom här skivornas volym mellan 2 utsatta gränsvärden detta gör att vi får en summerad volym med väldigt liten felmarginal eftersom vi har höjden på skivorna är så liten så att det inte spelar någon roll, den metoden är så gott som exakt om man jämför med trapetsmetoden eller rektangelmetoden där stora felmarginaler bildas
dunderklumpen1 skrev:Det är mest det som gör mig osäker på mina svar i uppgifterna, liksom har jag beräknat rätt volym nu
Metoden är att kurvan delas upp i skivor med med en höjd som går mot noll sedan beräknas summan av dom här skivornas volym mellan 2 utsatta gränsvärden detta gör att vi får en summerad volym med väldigt liten felmarginal eftersom vi har höjden på skivorna är så liten så att det inte spelar någon roll, den metoden är så gott som exakt om man jämför med trapetsmetoden eller rektangelmetoden där stora felmarginaler bildas
Då vi låter partitionens storlek gå mot noll kommer vår summa bli en riemannsumma (något som kräver vissa omskrivningar för att se) som konvergerar mot areans exakta värde, alltså det är ingen approximation. Detta är faktiskt inte helt trivialt och kräver en bra definition av volym samt en sats som säger att alla kontinuerliga funktioner är riemannintegrerbara. Resonemanget ovan är alltså inte helt fullständigt så det är inte helt konstigt att det känns lite som "magi"
Men om vi utgår i från Matematik 4 kursens läroplan hur lyder den "mest utförliga" förklaringen av saken i fråga isåfall?
Som ItzErre nämnde ovan kan man utgå ifrån Riemannsummor. Vi börjar med att ta gränserna och dela in varje segment i ett ändligt antal . Då kan vi approximera volymen med:
,
där är x-koordinaten i den högraste änden av varje disk.
Hur exakt vår volym blir beror helt och hållet på hur många indelningar vi väljer att göra, dvs. ett större värde på leder till en exaktare approximering. Nu kan vi ta gränsvärdet av denna summa då och erhåller då:
När man tar gränsvärdet slutar det alltså vara en approximering!
Du kan läsa mer om Riemannsummor här.
Hade ingen aning om Riemannsummor måste ha missat det i avsnittet, läser matte 4 på komvux distans allt jag har å utgå ifrån är boken å Youtube i stort sett hehe.
Tack så mycket för förklaringen kl 01:26 på natten <3
edit: tack för din förklaring också Erre!
Jag är osäker på om Riemannsummor ingår i kursen egentligen. Vissa lärare väljer att ta med det för ökad förståelse, andra kanske inte.
Vi kan vara mer exakta en så: (:
Om vi vet att vår summa blir en konvergent riemannsumma vilket den blir om f är kontinuerlig behöver vi aldrig approximera:
Tänk dig en väldigt liten indelning av vår rotationskropp. Ett segment kommer få den exakta arean
. Att detta stämmer tror jag går att påvisas med medelvärdesatsen, men fundera gärna själv varför det blir så geometriskt.
Om vi summerar alla dessa bitar och låter indelningen gå mot noll kommer summan bli vår integral
Okej så var felet i min förklaring att jag sa att skivorna går mot noll, där jag igentligen borde ha sagt oendligheten?
att vi delar upp arean under kurvan i antal rektanglar där
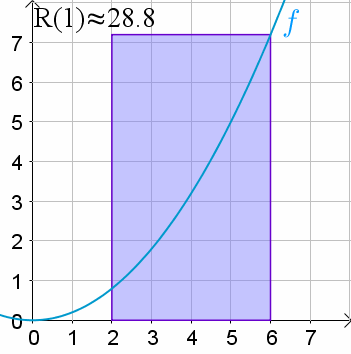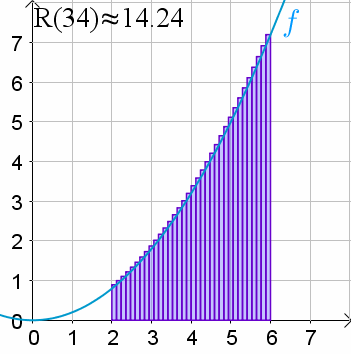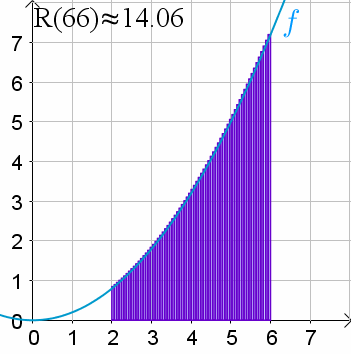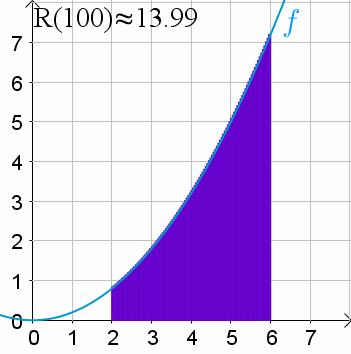
dom förklarade det så fint i nayttes länk



