Rotationsvolymer b) uppgiften

 Det blir ju lättare om grafen roterar kring y-axeln vilket jag vill komma fram till, alltså att skriva en ny funktion där kurvan roterar kring y-axeln. Men jag förstår inte riktigt hur jag ska tänka
Det blir ju lättare om grafen roterar kring y-axeln vilket jag vill komma fram till, alltså att skriva en ny funktion där kurvan roterar kring y-axeln. Men jag förstår inte riktigt hur jag ska tänka
fysik3 skrev:
Det blir ju lättare om grafen roterar kring y-axeln vilket jag vill komma fram till, alltså att skriva en ny funktion
Vad är det för funktion du har ritat upp? Den ser inte ut som , den funktionen borde gå genom origo.
kan den här bilden vara till hjälp?
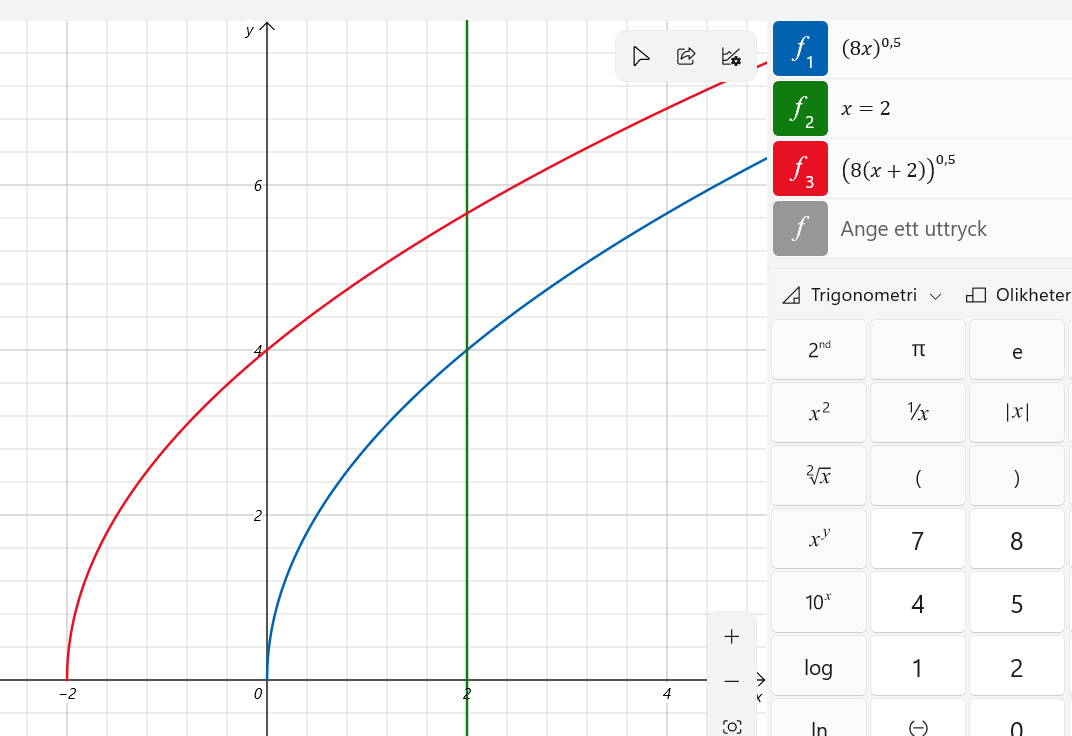
jag har sett lösningsförslaget men jag förstår inte riktigt hur man kommer fram till att det ska vara (8(x+2))^0.5
Jag har skrivit ner utförligt hur jag har tänkt. Är det rätt?
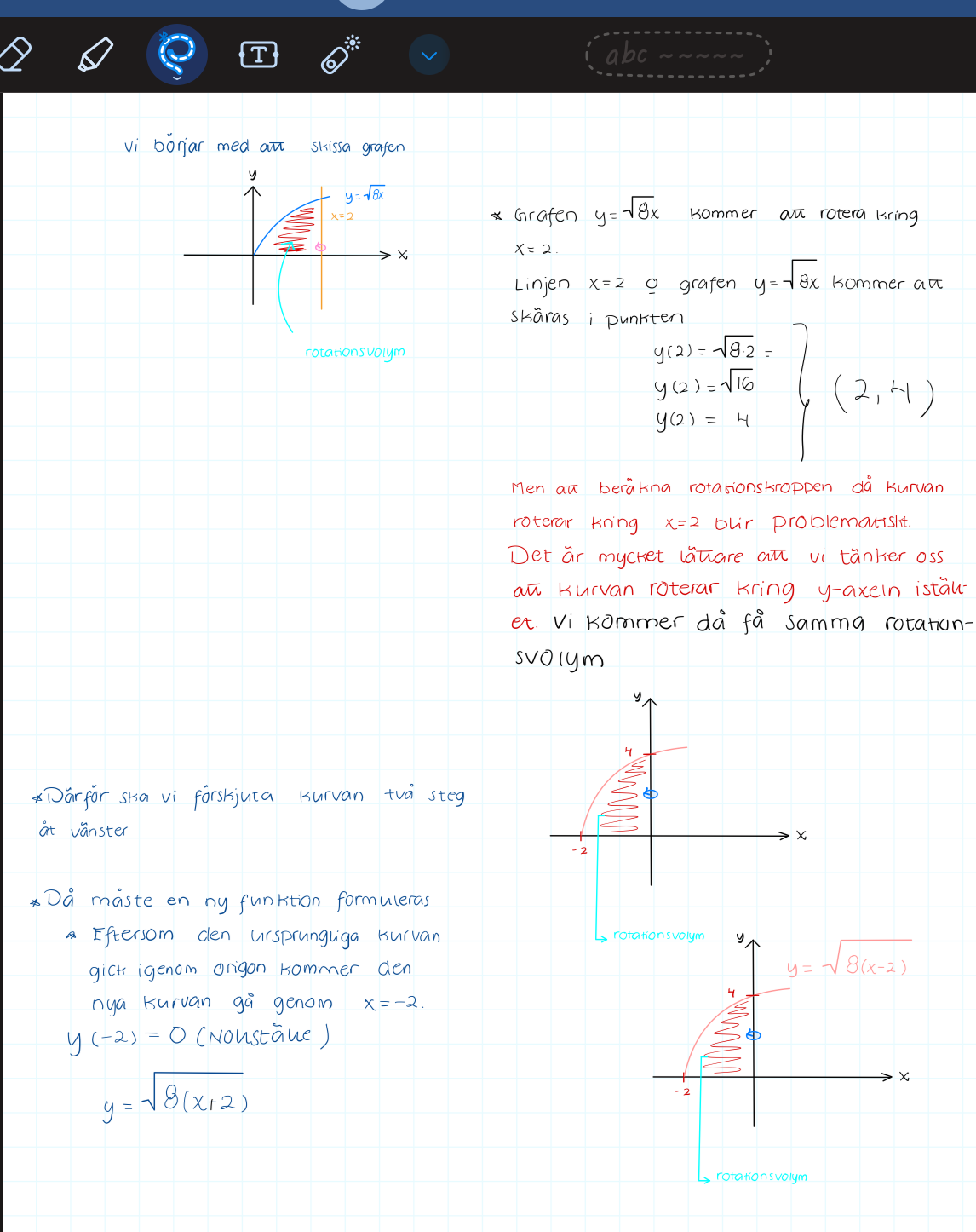

Ja, det ser rätt ut, förutom två felskrivningar som inte påverkar resutatet.
Här ska det stå plus istället för minus under rotenurtecknet:

Eftersom radien är lika med så ska det stå här:

Men pröva gärna att låta grafen ligga kvar som den gör i ippgiftslydelsen. Då blir radien och du kommer fram till samma integral utan tidsödande och felbenägna funktionsomskrivningar. Det är bra träning.
Du skulle alternativt kunna ställa upp integralen med avseende på och då skulle det bli:
Om jag inte tänker knasigt.
Tillägg: 19 apr 2024 13:44
Hoppsan, jag såg nu att Yngve i princip hade skrivit det redan.
naytte skrev:Du skulle alternativt kunna ställa upp integralen med avseende på och då skulle det bli:
Om jag inte tänker knasigt.
Nej, det stämmer. Det är enligt skalmetoden.
Tillägg: 19 apr 2024 13:44
Hoppsan, jag såg nu att Yngve i princip hade skrivit det redan.
Nej, det var inte samma.
Nej, det stämmer. Det är enligt skalmetoden.
Det vet jag inte vad det är men vad bra att det stämmer!
Nej, det var inte samma.
Hoppsan x 2. Jag läste bara "radien blir " och antog att du hade skrivit om samma sak. Dumma mig!
naytte skrev:
Det vet jag inte vad det är men vad bra att det stämmer!
Snyggt! Då satte du direkt en tillämpning av skalmetoden utan att känna till vad det är!
(Ursprungslösningen var ju enligt skivmetoden).
Dumma mig!
Absolut inte.
Ah, coolt! Visste inte att det fanns ett namn eller att det var en "metod", men det är väl rimligt eftersom det är det mest uppenbara sättet att angripa sådana problem på.
Jag brukar skapa en summa i mitt huvud som motsvarar volymen, "låtsas" att det är en Riemannsumma och sedan matcha elementen i summan mot motsvarande element i en integral. I just detta fall får man ju:
Och det verkar ju vara precis så de gör i länken du delade i ditt inlägg!
Som sagt, snyggt!
Yngve skrev:Ja, det ser rätt ut, förutom två felskrivningar som inte påverkar resutatet.
Här ska det stå plus istället för minus under rotenurtecknet:
Eftersom radien är lika med så ska det stå här:
Men pröva gärna att låta grafen ligga kvar som den gör i ippgiftslydelsen. Då blir radien och du kommer fram till samma integral utan tidsödande och felbenägna funktionsomskrivningar. Det är bra träning.
I facit står det att radien ska vara (y^2/8 - 2)^2 och inte (2 - y^2/8)^2
Kolla integrationsgränserna.
Smaragdalena skrev:Kolla integrationsgränserna.
förstår inte vad du menar, i facit står det samma som jag har kommit fram till 
Aha, jag tänkte fel. Det blir samma sak eftersom det är i kvadrat.
fysik3 skrev:I facit står det att radien ska vara (y^2/8 - 2)^2 och inte (2 - y^2/8)^2
Kan du ladda upp en bild på lösningen I facit?
Yngve skrev:fysik3 skrev:I facit står det att radien ska vara (y^2/8 - 2)^2 och inte (2 - y^2/8)^2
Kan du ladda upp en bild på lösningen I facit?
finns inte lösningen utan bara svaret men fredrik lindmark löser uppgiften på yt https://www.youtube.com/watch?v=r01XvmubVUY
fysik3 skrev:
finns inte lösningen utan bara svaret men fredrik lindmark löser uppgiften på yt https://www.youtube.com/watch?v=r01XvmubVUY
OK, när Fredrik sätter upp integralen räknar han med att radien är lika med x, men eftersom x är ett negativt tal då y < 4 så är radien där lika med -x.
Efrersom radien kvadreras så blir resultatet detsamma, men jag tycker att det är fel att skriva x istället för -x utan att förklara varför.






