rotationsvolym runt x och y axel
Kurvan y=√x och linjerna y=2 samt x=6 begränsar det område som är skuggat i figuren nedan.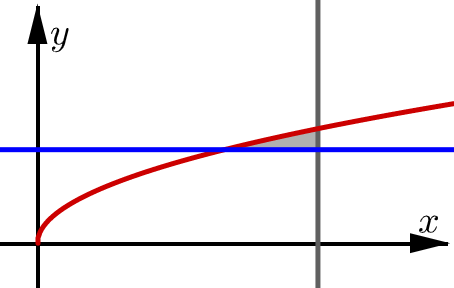
Beräkna volymen som uppstår när området roterar kring:
såhär gjorde jag för x-axeln: ∫64π(√x-2)2och sedan räknade ut det till ca -150 men det är ju långt ifrån svaret i facit som är 2π. Jag vet inte vad jag har gjort för fel.
och för y-axel blir det väll såhär: ∫√60π(y+2)4
Om du kör skivor kring x-axeln så behöver man beräkna rotationsvolymen för den yttre kurvan och ta bort rotationsvolymen för den inre kururvan.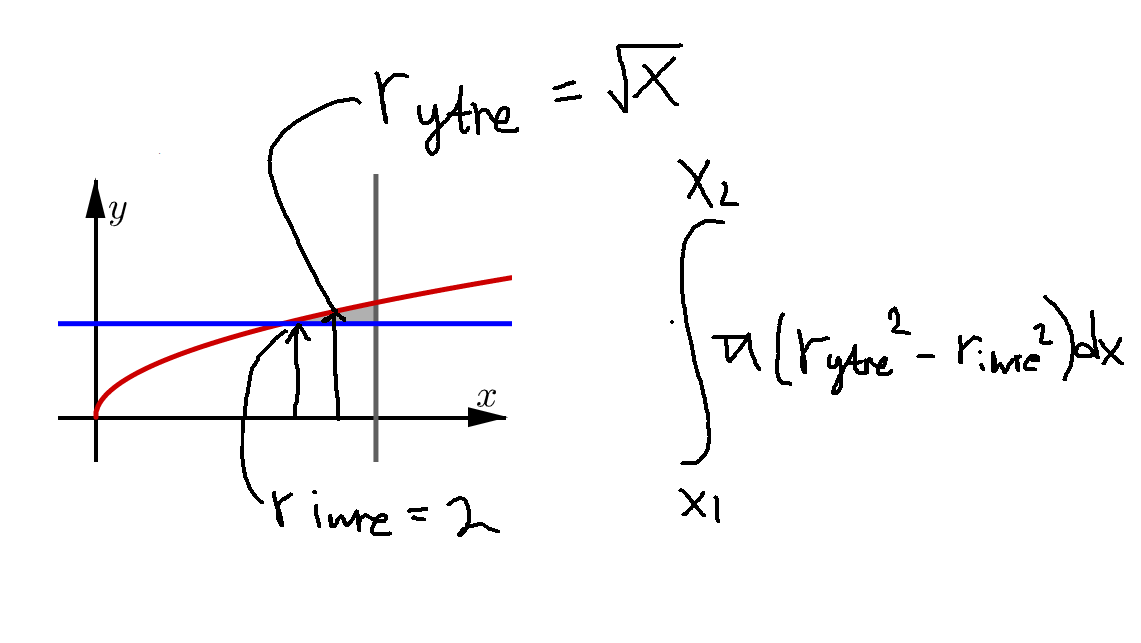
Att räkna på sättet du gör skulle ge rotationsvolymen om området roterade kring linjen x = 2.
Skivor kring y-axeln fungerar på samma sätt att man måste ta (r_ytre)^2 minus (r_inre)^2.
Lasse Vegas skrev:Skivor kring y-axeln fungerar på samma sätt att man måste ta (r_ytre)^2 minus (r_inre)^2.
när jag tar -2 så flyttas den ner till x axeln och jag behöver inte räkna inre. Borde jag inte fortfarande få samma svar?
bolibompa skrev:Lasse Vegas skrev:Skivor kring y-axeln fungerar på samma sätt att man måste ta (r_ytre)^2 minus (r_inre)^2.
när jag tar -2 så flyttas den ner till x axeln och jag behöver inte räkna inre. Borde jag inte fortfarande få samma svar?
Nej, du skapar en helt ny kropp då som ej nödvändigtvis har samma volym.
Trinity2 skrev:bolibompa skrev:Lasse Vegas skrev:Skivor kring y-axeln fungerar på samma sätt att man måste ta (r_ytre)^2 minus (r_inre)^2.
när jag tar -2 så flyttas den ner till x axeln och jag behöver inte räkna inre. Borde jag inte fortfarande få samma svar?
Nej, du skapar en helt ny kropp då som ej nödvändigtvis har samma volym.
ok, så då ska man ta både övre och den funktionen under upphöjt till två gånger pi, sedan samma sak med y-axeln fast sedan bryta ut x ur funktionerna
bolibompa skrev:Trinity2 skrev:bolibompa skrev:Lasse Vegas skrev:Skivor kring y-axeln fungerar på samma sätt att man måste ta (r_ytre)^2 minus (r_inre)^2.
när jag tar -2 så flyttas den ner till x axeln och jag behöver inte räkna inre. Borde jag inte fortfarande få samma svar?
Nej, du skapar en helt ny kropp då som ej nödvändigtvis har samma volym.
ok, så då ska man ta både övre och den funktionen under upphöjt till två gånger pi, sedan samma sak med y-axeln fast sedan bryta ut x ur funktionerna
Ja, som #2 beskriver. När det blir enkla kroppar som en cylinder behöver du inte integral, det finns färdig formel. Mindre chans till att räkna fel.
Trinity2 skrev:bolibompa skrev:Trinity2 skrev:bolibompa skrev:Lasse Vegas skrev:Skivor kring y-axeln fungerar på samma sätt att man måste ta (r_ytre)^2 minus (r_inre)^2.
när jag tar -2 så flyttas den ner till x axeln och jag behöver inte räkna inre. Borde jag inte fortfarande få samma svar?
Nej, du skapar en helt ny kropp då som ej nödvändigtvis har samma volym.
ok, så då ska man ta både övre och den funktionen under upphöjt till två gånger pi, sedan samma sak med y-axeln fast sedan bryta ut x ur funktionerna
Ja, som #2 beskriver. När det blir enkla kroppar som en cylinder behöver du inte integral, det finns färdig formel. Mindre chans till att räkna fel.
ok, tack för hjälpen!
