Rotationsvoly med skivmetod och skalmetod
Hej!
Jag skulle behövs hjälp med följande uppgift där jag ska räkna ut rotationsvolymen med både skalmetoden och skivmetoden och visa att metoderna ger samma resultat. Jag kommer fram till olika resultat och jag ser inte vad som har blivit fel.
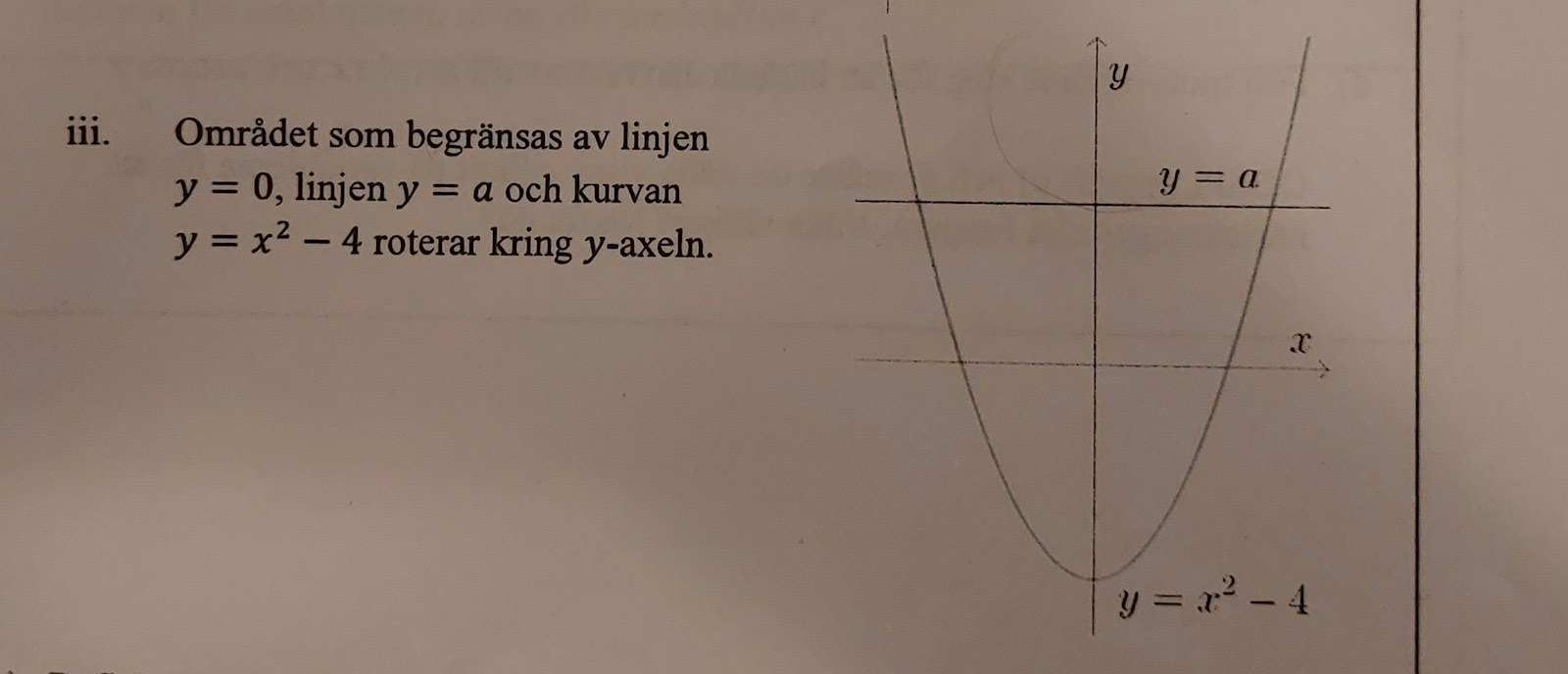

Tack på förhand!
Hej!
Kolla den här gränsen än extra gång

Hej!
Jag förstår inte riktigt vad du menar.
b tänker jag är den undre integrationsgränsen, dvs. från det y-värde grafen ska rotera runt y-axeln. Jag tänker mig att det är den gula ytan i bilden som roterar runt y-axeln.

linsun06 skrev:Hej!
Jag förstår inte riktigt vad du menar.
b tänker jag är den undre integrationsgränsen, dvs. från det y-värde grafen ska rotera runt y-axeln. Jag tänker mig att det är den gula ytan i bilden som roterar runt y-axeln.
Nä, jag skulle inte heller ha förstått vad jag menade om jag vore du... förlåt mig!
Jag läste uppgiften för snabbt helt enkelt, och jämförde bara de två volymer som du hade räknat ut.
Vilken volym har du räknat ut med skalmetoden? (vad är höjden på "cylinderskalet")
Jag har tänkt att jag har räknat ut den gula volymen i förra bilden, men det kanske inte stämmer.
Det jag har förstått är att skalmetoden räknar ut volymen på område mellan kurvan och x-axeln, vilket här isåfall bli området till höger om kurvan (till höger om det gula). Jag tänkte att jag kompenserade för det genom att ta a-(f(x)).
I x-intervallet när f(x) är negativ så måste beräkningen bli en annan för det stämmer inte, eller hur?
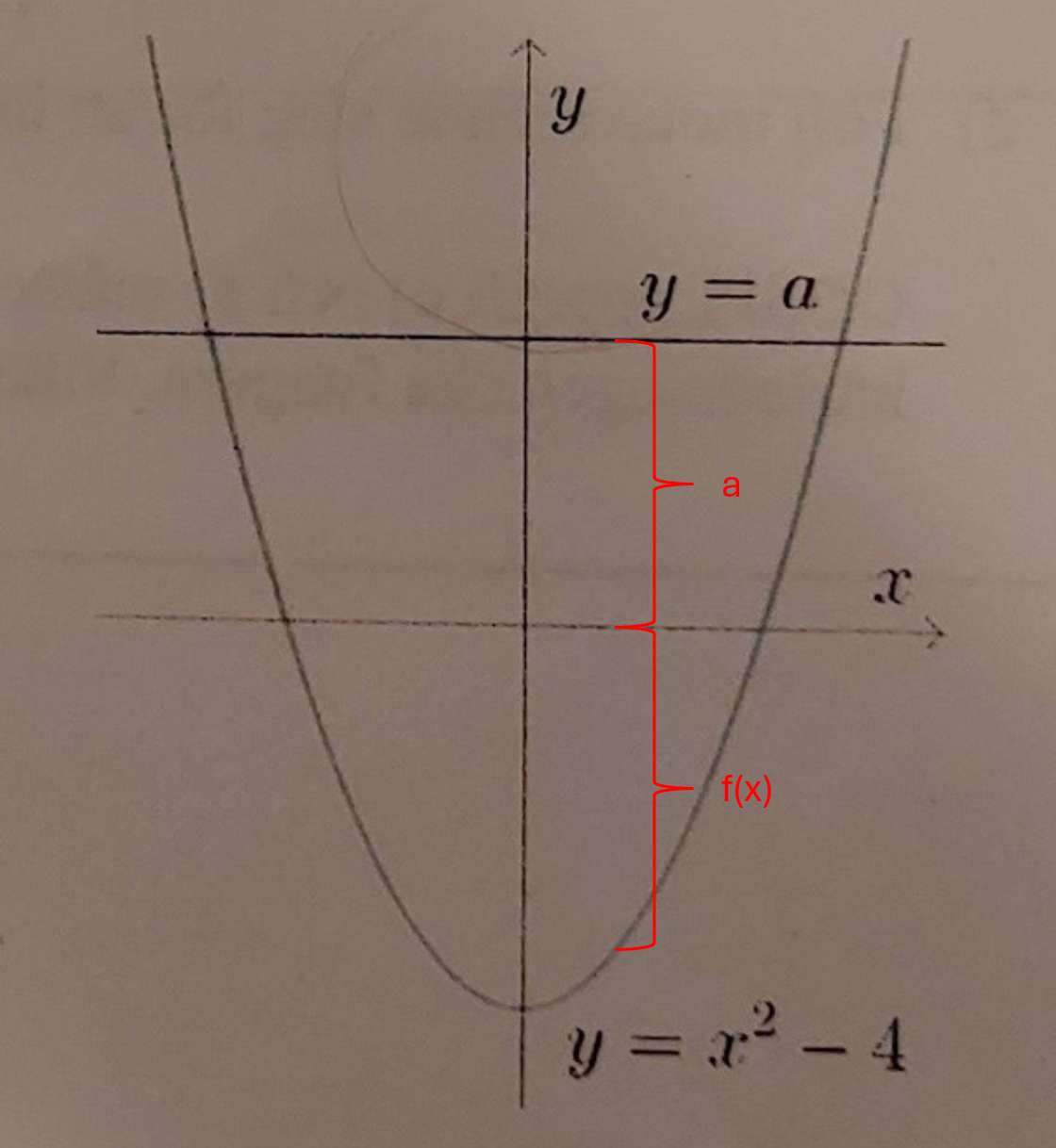
Ska jag räkna med området under x-axeln även om det enligt uppgiften inte ska roteras runt y-axeln?
Nej, området under x-axeln bidrar inte till rotationsvolymen i uppgiften.
Okej, det var som jag tänkte.
När jag bytat plats på integrationsgränserna till skalmetoden (dvs. bytat c till b och b till c) fick jag samma svar som när jag använde skivmetoden fast negativt. Är det något jag kan fundera vidare på eller är det bara en tillfällighet?
Jag tror du tänker lite fel, vi fortsätter såklart att förklara för dig.
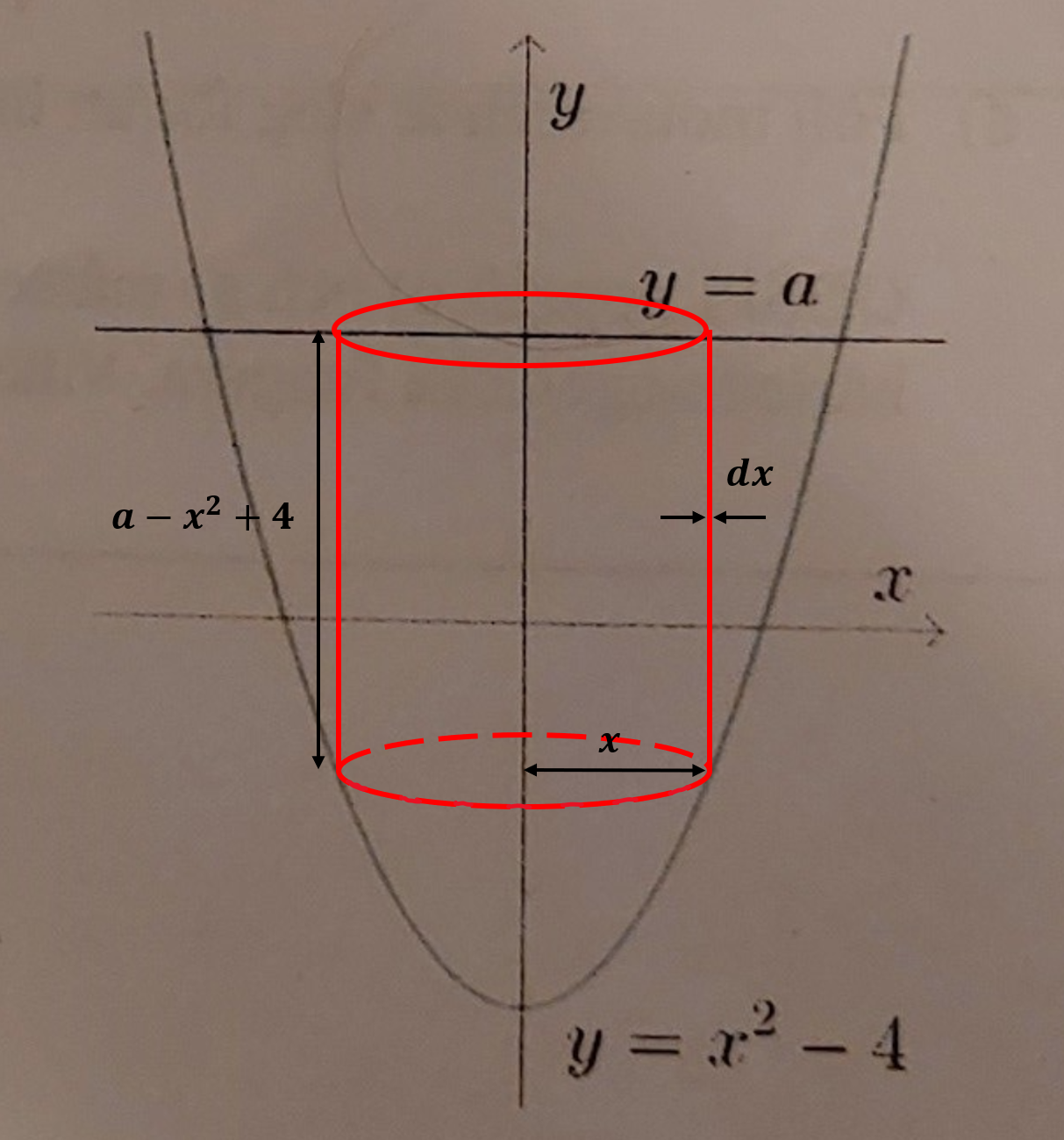
Skalmetoden betyder att man bildar "cylinderskal" med tjockleken dx, 0ch summerar alla dessa skal, från x=0 till yttre gränsen på rotationsvolymen, som jag har försökt rita i figuren nedan.
Ditt första försök med skalmetoden beräknade därför volymen av hela rotationsvolymen ända till y=-4. (Det var därför jag trodde att du skulle beräkna hela rotationsvolymen med skivmetoden också. Därav mitt initiala missförstånd).
Ser du hur du nu hur du ska beräkna rotationsvolymen? (Det räcker alltså inte att byta integrationsgränser i ditt första försök med skalmetoden)
Tack så mycket för hjälpen, nu förstår jag lite bättre!
Så för varje x jag väljer som radie i cylindern kommer jag räkna med en del som är under x-axeln också?
Höjden i cylinders motsvaras av f(x) i formeln för rotationsvolym. V=2π∫abx⋅f(x)dx
Jag är osäker på vad min höjd kommer motsvaras av. Höjden av cylindern under x-axeln kommer väl att vara f(x) där x är radien är cylindern? Är höjden av cylindern ovanför x-axeln isåfall a, det vill säga höjden jag ska sätta in i formeln är a?
Höjden i cylinders motsvaras av f(x) i formeln för rotationsvolym. V=2π∫abx⋅f(x)dx
Ja precis! _Om_ f(x) är en funktion som är positiv på x-intervallet, så beskriver funktionen höjden på cylindern mellan funktionen och x-axeln. Hur det blir i alla andra fall måste man rita en figur för att förstå (iallafall jag måste rita en figur för att förstå). Så att när du beskrev att du försökte "kompensera", så visade det sig, när jag ritade en figur, att vad du egentligen gjorde var att beräkna även rotationsvolymen på den negativa delen av y-axeln.
Är höjden av cylindern ovanför x-axeln isåfall a, det vill säga höjden jag ska sätta in i formeln är a?
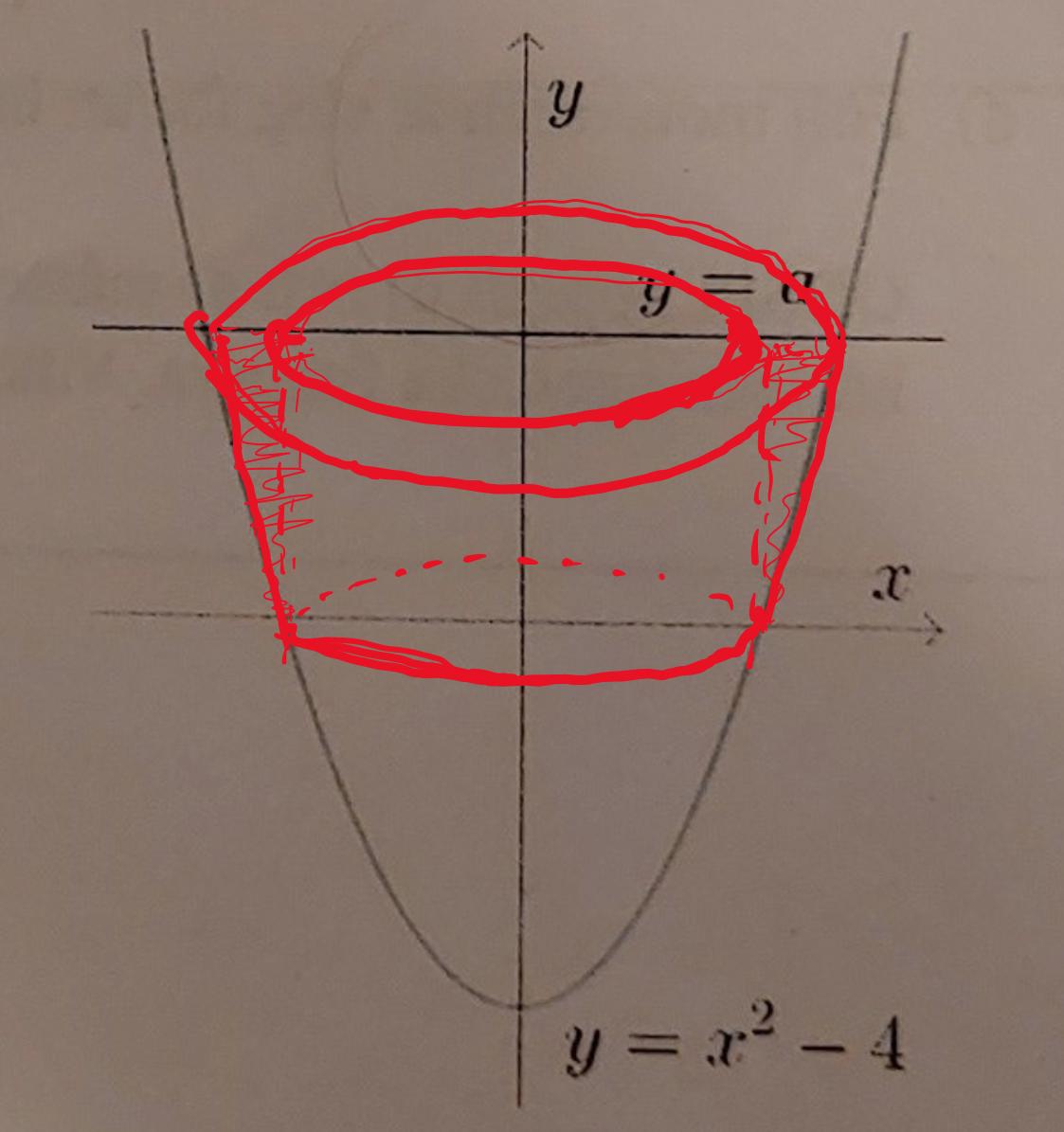
Ja precis! I det x-intervall som f(x) är negativ ska du sätta in a istället. Du måste alltså dela in x-intervallet i två x-intervall. Ett x-intervall där f(x) är positiv, och ett x-intervall där f(x) är negativ. Titta på min bild nedan, förstår du något av den? (den blev ganska kluddig...)
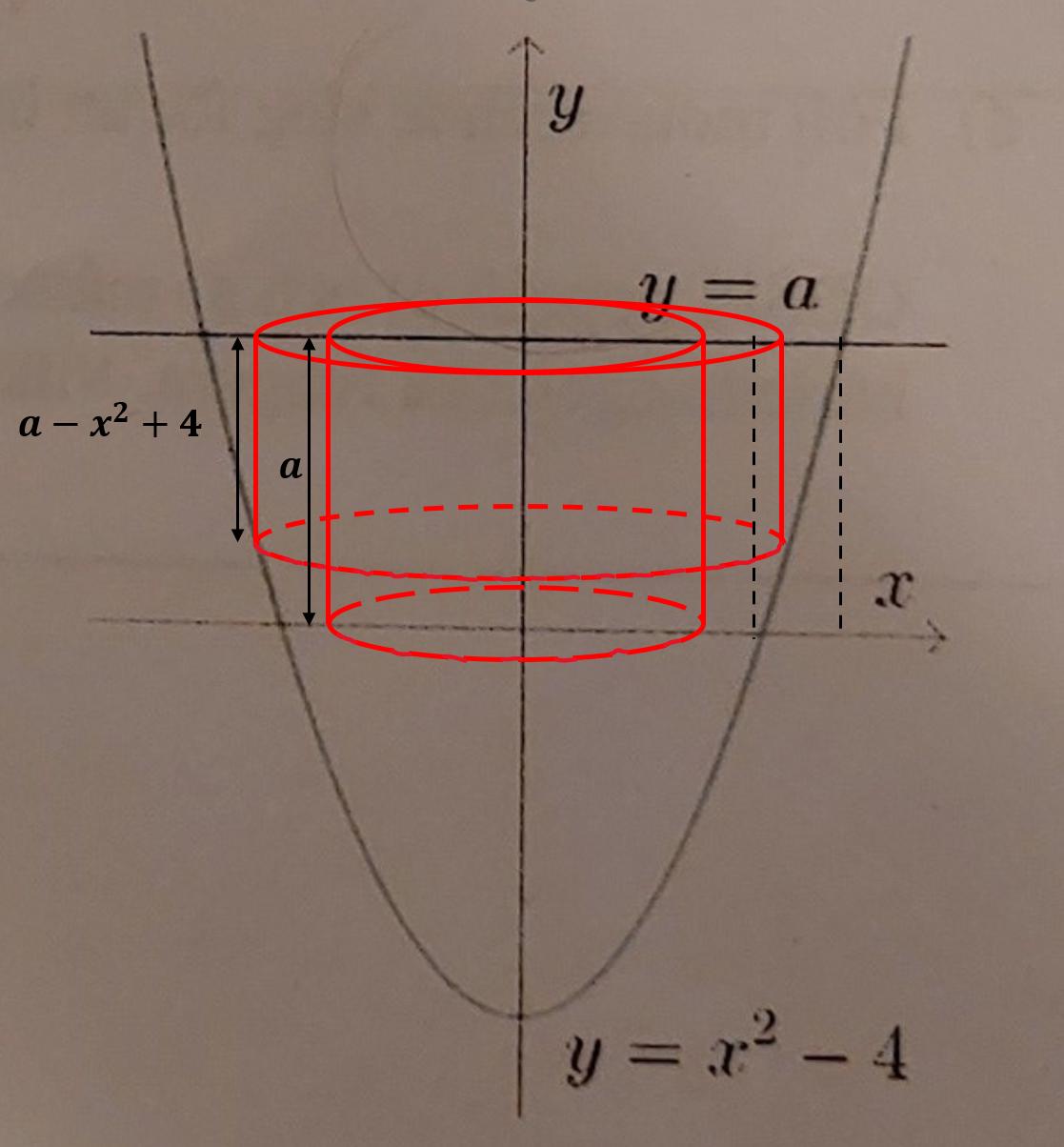
Tack för hjälpen, men jag är ganska förvirrad just nu.
Är inte f(x) positivt hela tiden så länge man är ovanför x-axeln?
Jag försöker förklara på annat sätt.
Man måste dela upp beräkningen av rotationsvolymen på två x-intervall, eftersom i första intervallet bestäms cylinderskalets höjd av linjen y=a dvs höjden=a, vilket ger volymen av en solid cylinder:
V1=2π∫20axdx
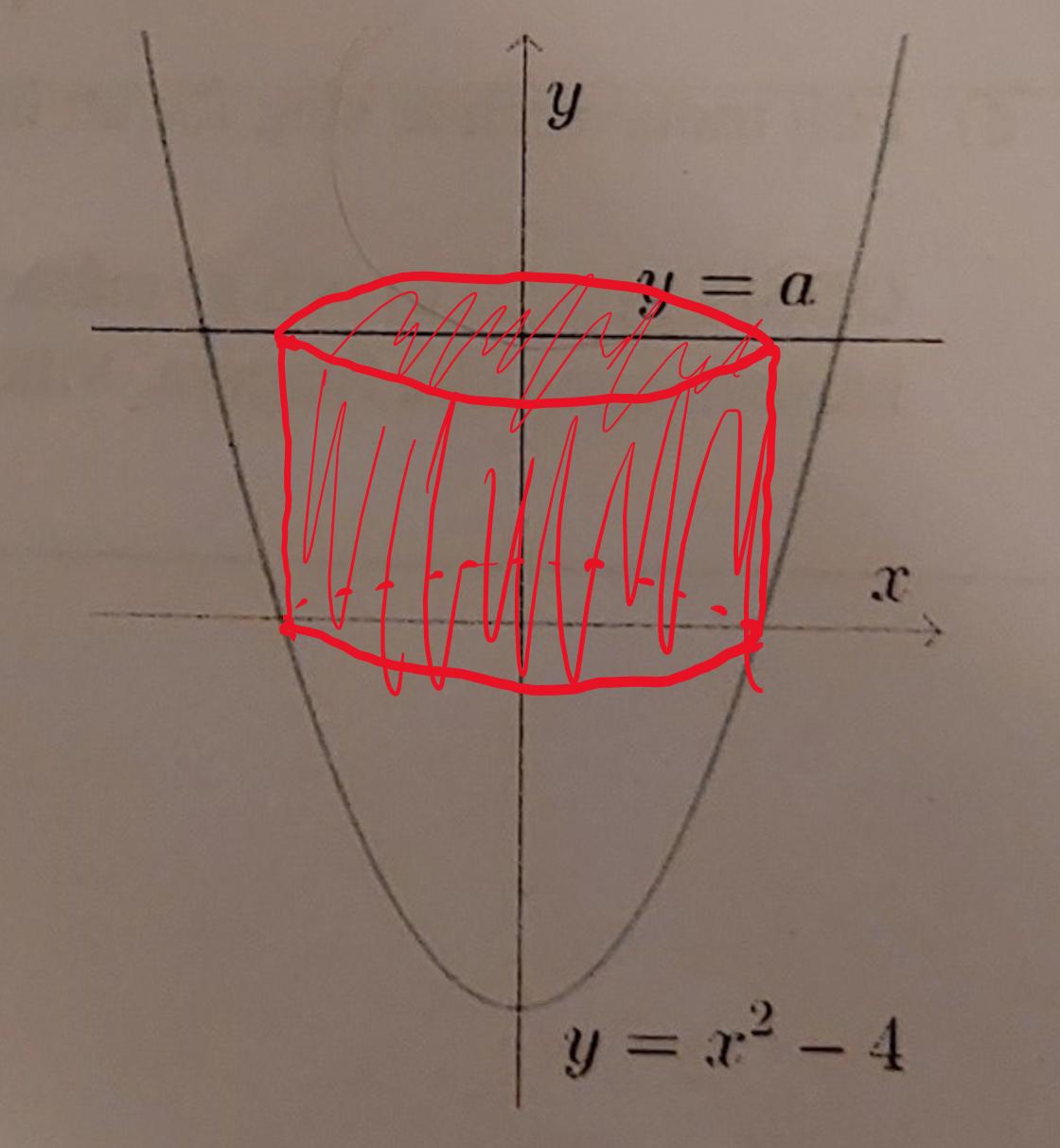
Samt ett x-intervall där cylinderskalets höjd bestäm av linjen y=a, och kurvan y=x2-4, dvs höjden=a-(x2-4), vilken ger ett slags ihåligt rörformad volym:
V2=2π∫√a+42x(a-(x2-4))dx
Tack så mycket för förklaringen och för all hjälp!
Nu förstår jag hur det fungerar.
Hoppas också att svaret stämde! 👍
Svaret stämde med det jag fick när jag använde skivmetoden.
Kanon!
Då kanske du också ser att du räknade ut den totala volymen (dvs även den delen av volymen som finns längs negativa y-axeln) i ditt första försök med skalmetoden i trådstarten?



