rotationsintegraler
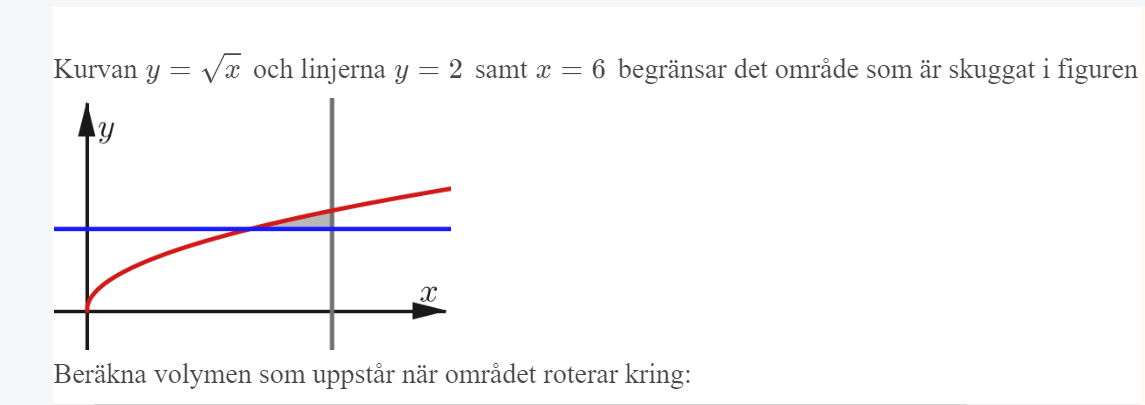
b) när den roterar runt y axeln
jag förstod när det var runt x axeln för man skulle bara subtrahera kuben som bildas under den skuggade figuren från total volymen men jag förstår inte alls förklaringen till b) uppgiften.
eftersom det roterar runt y-axeln skrev jag om det till x = y^2 och ena ändpunkten är y = 2 och den andra är kvadratroten ur 6
jag kom fram till detta: ∫√62π och beräknade bara detta men jag förstår inte varför svaret är fel
Hej.
Orsaken till att det blir fel är att du då beräknar något annat än det som avses.
Det ser ut som om du försöker beräkna volymen som bildas då det gråstreckade området som jag markerat i bilden roterar ett varv runt y-axeln.
Men i så fall är integranden fel.
En sådan cirkelskiva har ju radien vilket betyder att skivans area är , dvs .

Men du kan ju använda ditt tankesätt till att subtrahera den volym du beräknar från volymen av en större cylinder. Ser du hur?
Yngve skrev:Hej.
Orsaken till att det blir fel är att du då beräknar något annat än det som avses.
Det ser ut som om du försöker beräkna volymen som bildas då det gråstreckade området som jag markerat i bilden roterar ett varv runt y-axeln.
Men i så fall är integranden fel.
En sådan cirkelskiva har ju radien vilket betyder att skivans area är , dvs .
Men du kan ju använda ditt tankesätt till att subtrahera den volym du beräknar från volymen av en större cylinder. Ser du hur?
jag ser verkligen inte... Sett facit och dom pratar i likanden spår som du och fattar inte vad för form dom vill att jag ska subtrahera från.
Titta på området som begränsas av y-axeln samt linjerna , och .
Låt detta område rotera ett varv runt y-axeln.
Den rotationskropp som då uppstår har formen av en cylinder med radie och höjd .
Är du med på det?



