Rotation kring x=-1

Kurvan y=x, Linjen y=2.

och y-axeln begränsar ett

område, Bestäm volymen om

detta område roterar kring x=-1

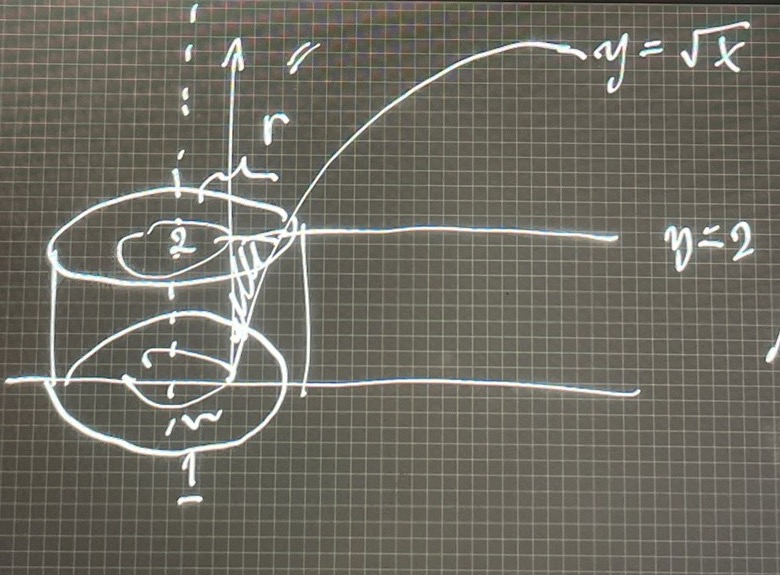Jag vet att jag måste ta hela volymen minus cylindern i mitten men jag har problem med att ta fram den hela volymen

blir det så här?

Om du låter en ny funktion definieras av $g(x)=2-\sqrt{x}$ kan du räkna på som vanligt om du funderar på var dina gränser borde hamna i förhållande till $x=-1$ .

Varför 2-√x ?

kan jag inte flytta grafen ett steg till höger så att den blir y = √(x-1) så att jag får rotation kring y axeln bara istället?

Jag vill föreslå ett helt annat tankesätt än att tänka i inre och yttre cylindrar, som jag personligen tycker är mycket enklare. Men försök med MrPotatoheads förslag först!

Titta här när du har försökt själv.

Jag tänker alltid att man delar in hela området i oändligt många, infinitesimalt breda "rektanglar" med bredd $\mathrm{d}x$ . Höjden på en sådan rektangel är i vårt fall $2-\sqrt x$ . Om man roterar rektangeln runt axeln och sedan klipper upp cylindern så får man ett rätblock, med måtten:

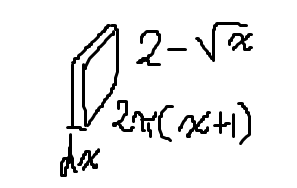
Man tänker att skivan är så tunn att man kan räkna på en "cirkels omkrets" (därifrån kommer $2\pi(x+1)$ ). Volymen på ett sådant rätblock är trivialt $2\pi\mathrm{d}x(x+1)(2-\sqrt x)$ . Så om vi summerar oändligt många sådana volymer kommer vi fram till en integral som ger volymen på rotationskroppen.

Tack! Sen hur räknar jag det vanligt med skivmetodem? Är det okej att flytta grafen ett steg som jag gjorde och sen räkna med rotation kring y axeln bara?

Svara

Visa senaste svar