Rotation av cirkelsektor kring y-axeln

Bilden är paj.

Nu!

Det är en sfär minus 2 "glass-strutar" med spetsen emot varandra. En glass-strut är är en rak cirkulär kon + en kalott. Det finns färdiga formler för detta.

Det går med sfäriska också. En vinkel går mellan 0 och 2pi, den andra mellan 0 och (pi/2-theta). r mellan och a. Dubbla sedan volymen.

Ja, jag försökte med den första. Färdiga formler får man nog inte använda så försökte härleda men det gick inte så bra.

Hur kan den gå från 0 till 2Pi? Hur ser den integralen ut?

MrPotatohead skrev:

Ja, jag försökte med den första. Färdiga formler får man nog inte använda så försökte härleda men det gick inte så bra.

Hur kan den gå från 0 till 2Pi? Hur ser den integralen ut?

I xy-planet roterar man ett helt varv och i xz-planet mellan 0 och pi/2-theta

Jag har tyvärr inte lärt mig hur man gör det. Är det metoden man kör i flervarre sen? Skulle du vilja visa hur integralen ser ut?

Det kommer i Flervariabelanalys, och ser ut i stil med

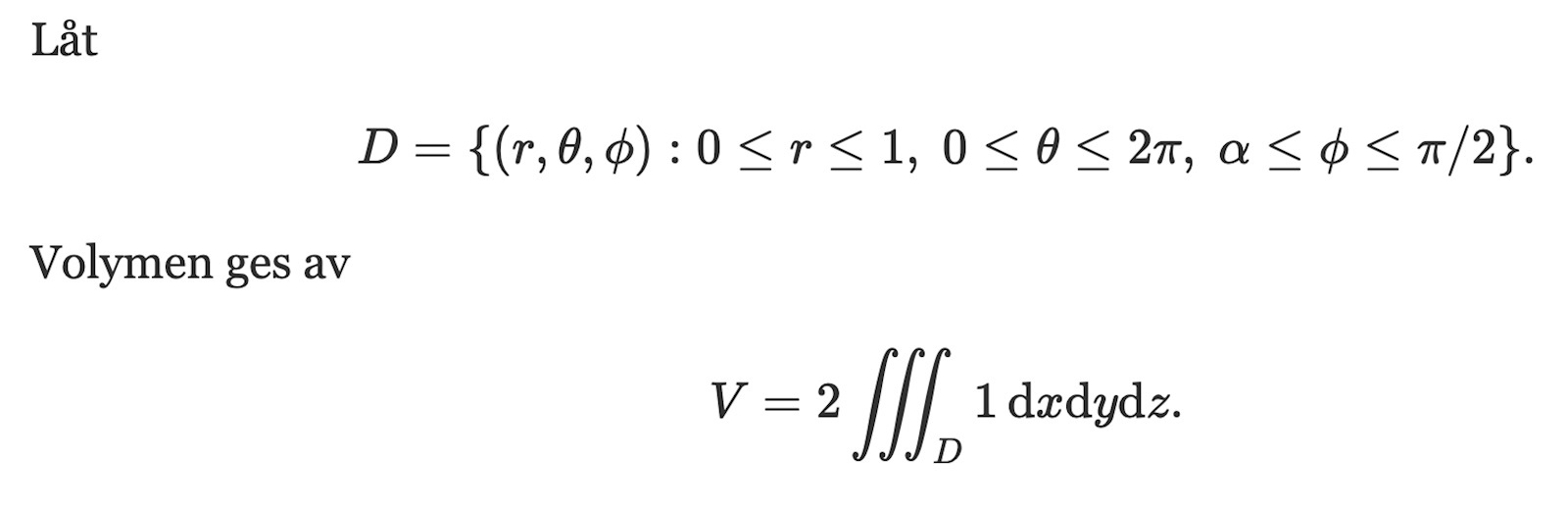
där jag använt beteckningar från

https://sv.wikipedia.org/wiki/Sf%C3%A4riska_koordinater

samt att kroppen är en spegling i xy-planet varför det räcker med att räkna på övre halvan och sedan multiplicera med 2.

alpha = ditt theta och radien a är r.

Men, det går att göra med gymnasiekunskaper/envariabelanalys. Du vet formeln för en rak cirkulär kon. Vad du behöver är en formel för en kalott, vilket är en bit cirkelbåge som roterar runt en axel. Det är en bra övning i analys som passar gymnasiet. Även om cirkelns ekvation y=sqrt(r^2-x^2) är "besvärlig" är det inget problem då man kvadrerar uttrycket för roterande kroppar och därmed är integranden enkel. Prova och så ger vi input om det går fel.

Vad är uppgiften här? Att använda rotationsvolymer? Du pratar om sfäriska koordinater, men det låter inte relevant för envariabelanalys.

Som Trinity2 är inne på är det bara att köra skiv-/skalmetoden rakt av:

Skivmetoden

$\displaystyle V = \int_{y_{min}}^{y_{max}}\left(x\left(y\right)\right)^2 \ dy$

Svårigheten kan då komma från att formulera $x(y)$ korrekt men om man ritar lite så går det nog bra. 

Stort tack Trinity2. Ska försöka på både en- och flervarremetoden. Hör av mig om det strular.

—-

Uppgiften är från mekanikkursen. Jag uttryckte mig fel, menade polära koordinater. Det jag ville var att ställa upp en integral som beror på en vinkel för det kändes som att det skulle göra uppgiften jättelätt + att jag var nyfiken på hur en sådan integral skulle se ut. Men det kanske var fel  tänkt.

Jag testade skivmetoden utan framgång. Förmodligen slarvade jag någonstans, ska försöka igen. Tack för ditt svar. :)

Ååååå, det löste sig. Jag behövde bara vara lite noggrann, och använda korrekt metod.. Stort tack gänget! :)

Tillägg: 5 dec 2024 22:47

Det saknas förresten ett pi i din skivmetod SaintVenant om du vill ordna för framtida åskådare. 

För andra:

Denna uppgiften kunde tydligen lösas på några rader med

https://en.wikipedia.org/wiki/Pappus%27s_centroid_theorem 

MrPotatohead skrev:

För andra:

Denna uppgiften kunde tydligen lösas på några rader med

https://en.wikipedia.org/wiki/Pappus%27s_centroid_theorem 

Jag har inte satt mig in i texten men är det verkar intressant. Vet ej varför denna ej har fokus i matematikutbildning (har aldrig sett den i någon bok). Men tiderna förändras och geometri anses inte så viktigt numera. Möjligtvis är den begränsad i sin användning och den mera generella metoden med polära koordinater är bättre.

Kanske fel av mig att lägga tråden i envariabelanalys. Det är ju en mekanikfråga i området om tyngdpunkt. Tänkte att de matametiska metoderna man fått lära sig är de bästa. Oavsett hade folk som känner till den kanske lättare kunnat göra kopplingen då. Jag hade i alla fall inte heller någon aning om att den fanns. Vår föreläsare nämnde den inte alls men den gömde sig tydligen i kursboken (som ingen använder)...