rörelseenergi och rörelsemängd

vilken formel bör jag använda mig utav?
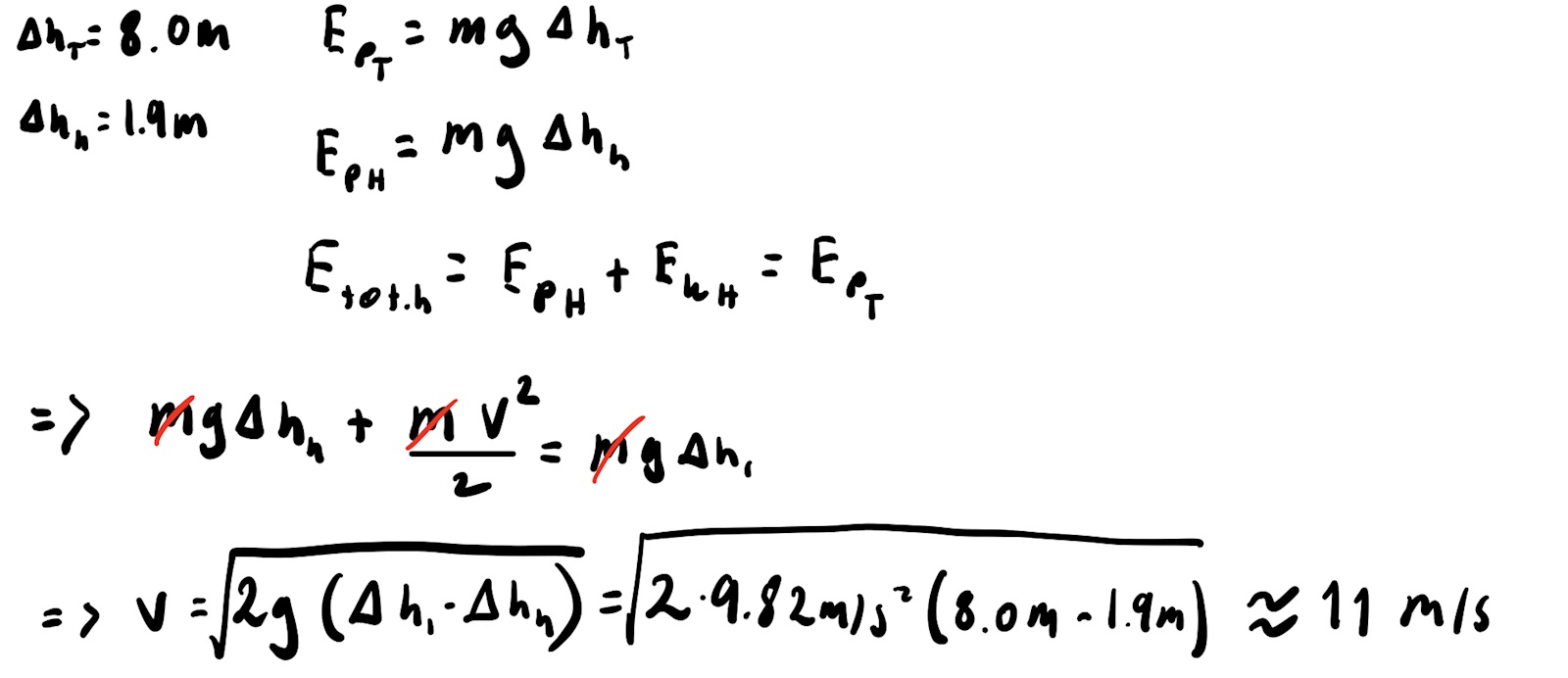
står såhär i lösningsförslaget men förstår inte hur man får ut v i formeln och vad denna formeln heter
De har använt uttrycket för lägesenergi () och uttrycket för rörelseenergi ().
Vidare har de använt sig av energiprincipen, det vill säga att energi inte kan försvinna, endast omvandlas.
naytte skrev:De har använt uttrycket för lägesenergi () och uttrycket för rörelseenergi ().
Vidare har de använt sig av energiprincipen, det vill säga att energi inte kan försvinna, endast omvandlas.
kan du hjälpa mig förstå hur de har omvandlat med hjälp av formlerna? jag förstår inte hur processen går till
Jag tycker att lösningsförslaget är onödigt komplicerat.
Sätt = hastigheten när mobilen lämnar kasthanden, dvs det som efterfrågas.
Rörelseenergin när mobilen lämnar kasthanden är då
Sätt = kastets höjd ovan utkastpunkten, dvs höjdskillnaden mellan högsta punkten och utkastpunkten.
När mobiltelefonen når sin högsta punkt har lägesenergin ökat med
Samtidigt har rörelseenergin minskat till 0, eftersom mobiltelefonens hastighet är 0 precis när den vänder vid högsta punkten.
Ökningen i lägesenergi är precis lika stor som minskningen i rörelseenergi, vilket ger oss ekvationen
Efter förenkling får vi ekvationen
Eftersom m så får vi
Yngve skrev:Jag tycker att lösningsförslaget är onödigt komplicerat.
Sätt = hastigheten när mobilen lämnar kasthanden, dvs det som efterfrågas.
Rörelseenergin när mobilen lämnar kasthanden är då
Sätt = kastets höjd ovan utkastpunkten, dvs höjdskillnaden mellan högsta punkten och utkastpunkten.
När mobiltelefonen når sin högsta punkt har lägesenergin ökat med
Samtidigt har rörelseenergin minskat till 0, eftersom mobiltelefonens hastighet är 0 precis när den vänder vid högsta punkten.
Ökningen i lägesenergi är precis lika stor som minskningen i rörelseenergi, vilket ger oss ekvationen
Efter förenkling får vi ekvationen
Eftersom m så får vi
tack så mycket för svaret



