Rörelse

Likformig acceleration beräknas genom, $a=\frac{∆v}{∆t}=\frac{v_2-v_1}{t_2-t_1}$. Man ska alltså ta skillnaden i hastighet och dela med skillnaden i tid. Hur mycket har hastigheten förändrats mellan v0 och v1?

Hastigheten har minskat med 0,30 m/s efter 1,20 sekunder. Δv är därav 0,30 m/s

Δt=1,20-0 = 1,20 s

så då blir a= 0,30 / 1,20 = 0,25 m/s²

^v₀=5m/s

sedan kan man beräkna sträckan med

s=v₀•t+(a•t²/2)

s=6,18 m

därav tid att stanna med hastigheten 4,70 m/s, blir

6,18/4,70= 1,3 sekunder 

?

eller ska man addera förfluten tid också så totalt 1,20+1,3 = 2,5 sekunder tills pucken stannar

Storleken på accelerationen är rätt men det ska vara ett minustecken också. Hastigheten minskar ju.

Ser ut som du räknar ut sträckan för de första 1.2s, men det är sträckan till pucken stannar som det frågas efter.
Det finns en annan formel med v, v₀, a och s. Vet du vilken?

Den sista fungerar bara om hastigheten är konstant 4.7m/s

just ja.

Δv är  4,70-5,00= -0,30 m/s

så då blir a= -0,30 / 1,20 = -0,25 m/s²

^v₀=5m/s

sedan kan man beräkna sträckan med

s=v₀•t+(a•t²/2)

s=5,82 m

Jag kommer inte ihåg om den andra formel.

eller är det v=v₀•at

men v byts ut till delta s/ delta t

I min gamla formelsamling finns: $v^2 = {\left(v_0\right)}^2 + 2as$.

Jag är obekant med den formeln.

Längst ner i din första bild så finns den.

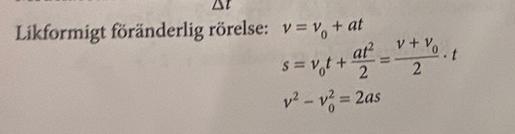
Skriven lite annorlunda, men samma sak

Så då

man har räknat ut a=-0,25m/s²

sedan kan man beräkna sträckan med

v²- v₀=2•a•s     =>     s=(v²- v₀)/(2•a)

s=5,82 m

därav tid att stanna med hastigheten 4,70 m/s, blir

5,82/4,70= 1,23 sekunder 

eller ska man ta med redan förflutet tid 1,23+1,20= 2,43 sekunder tills pucken stannar?

v₀ ska också vara i kvadrat. Jag får sträckan till: $s = (v^2 - {\left(v_0\right)}^2)/2a = (0 - 25)/2(-0.25) = 50m$

I sista steget tror jag det är enklast att räkna ut medelhastigheten, sträckan har du så då kan man räkna ut tiden.

Ok, men är inte v=4,7 m/s och v₀=5,00 m/s ?

v har sjunkit till 4.7m/s efter de första 1.2 sekunderna. När pucken glider vidare och till slut stannar  är v = 0.

då blir det v_m=s/t  => 50m/1,2 s ?

Nej tyvärr.
Vi börjar med 5m/s och slutar med 0m/s. Med acceleration på -0.25m/s² så sjunker hastigheten linjärt ner till noll.

ThomasN skrev:

v₀ ska också vara i kvadrat. Jag får sträckan till: $s = (v^2 - {\left(v_0\right)}^2)/2a = (0 - 25)/2(-0.25) = 50m$

I sista steget tror jag det är enklast att räkna ut medelhastigheten, sträckan har du så då kan man räkna ut tiden.

Det sista steget:

Sträckan då hastigheten 4,70 m/s går mot 0 m/s. Och pucken stannar till slut  är beräknad.

s=50

Acceleration minskningen är på -0,25 m/s² under den sträckan.

för att beräkna tiden t så behövs v_m räknas ut.

Jag vet att också att sträckan är för de första 1.2s, är 6,18 m.

Sträckan 50m är för hela rörelsen med hastigheten 5m/s ner till noll.

Medelhastigheten kan du räkna ut så här:

(Den blir helt enkelt 2.5m/s)

Sen kan du använda formeln v_m=s/t. Stuva om den så du får t = ...

tiden det tar för pucken att stanna då hastigheten 5,00 m/s går mot 0 m/s, under 50 meter . Och pucken stannar till slut är 20 sekunder 

t=s/v _m=> 50/2,5 = 20 sekunder 

ThomasN skrev:

Storleken på accelerationen är rätt men det ska vara ett minustecken också. Hastigheten minskar ju.

Ser ut som du räknar ut sträckan för de första 1.2s, men det är sträckan till pucken stannar som det frågas efter.
Det finns en annan formel med v, v₀, a och s. Vet du vilken?

Den sista fungerar bara om hastigheten är konstant 4.7m/s

påtal om Accelerationen:

Δv är  4,70-5,00= -0,30 m/s

Δt=1,20-0 = 1,20 s

så då blir a= -0,30 / 1,20 = -0,25 m/s²

Efter 1,20 sekunder så har pucken nått Max punkten av sin hastighet och därefter börjar hastigheten avta successivt tills det är noll. Därav behövde man räkna ut acceleration minskningen som pucken kommer ha fram tills pucken har nått 0m/s?

för att på så vis kunna räkna ut det totala sträckan då pucken hade 5m/s => 0m/s

Max hastigheten är den vi har i starten, 5m/s. Därefter sjunker hastigheten ända tills pucken stannar. Efter 1.2s har den sjunkit till 4.7m/s. Som du säger, de här värdena har vi fått för att kunna räkna ut accelerationen.

Att du orkar, imponerande!

Tack, så mycket för hjälpen.

Jag försöker förstå så gott jag kan. 

Nu är det nog dags att krypa till sängs, hoppas det klarnade lite.

Ser det här ut som en bra resonemang?

Helt rätt, perfekt! 

Och en mycket klar och tydlig redogörelse!