Rörelse
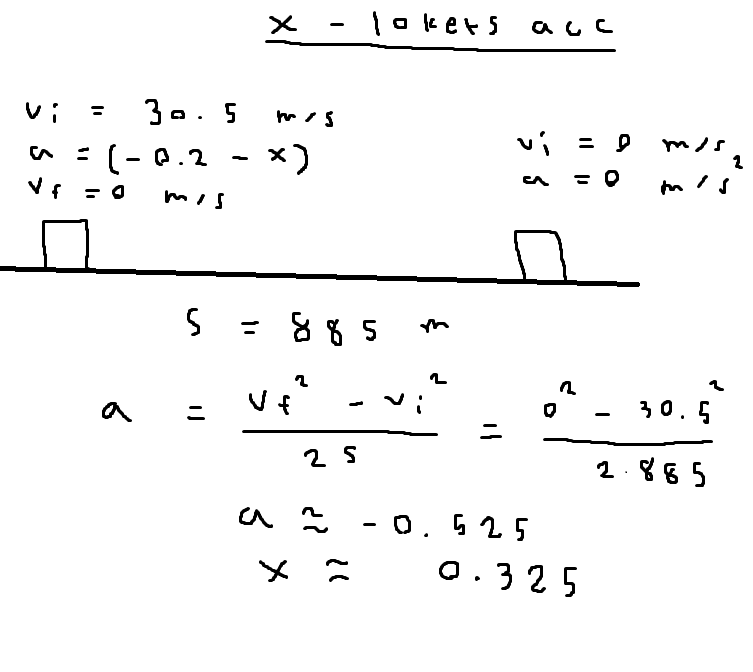
Föraren på ett tåg med hastigheten 117 km/h upptäcker ett stillastående lok 1200 m längre bort. Föraren börjar genast bromsa och signalerar samtidigt. 10 sekunder senare börjar äntligen loket att sätta sig i rörelse bort från tåget. Anta att de båda rörelserna är likformigt accelererade, och att tågets acceleration är -0,20 m/s2. Hur stor måste lokets acceleration minst vara för att enkollision skall undvikas?
Jag har ritat 3 olika situationer.
Innan, 10 sekunder efter och efter de 10 sekunderna har passerat.
Jag har kommit fram till en situation där jag har tåg A och tåg B.
Tåget A har en v=30.5m/s och a=-0.2m/s^2
Tåg B ska nu börja accelerera för att nå en hastighet som är =eller > är tåg A hastighet efter 885 m. Med andra ord tåg B har på sig 32.5 s för att nå det hastigheten.
Jag bygger mitt svar på antagandet ovan och skriver upp följande ekvation
Vilken ger en acceleration på 0.74m/s^2
Så tåg B måste ha en acceleration som är = eller > än 0.74 för att undvika en kollision.
Är antagandet rätt?
SaS.. skrev:Jag har ritat 3 olika situationer.
Innan, 10 sekunder efter och efter de 10 sekunderna har passerat.
Rita en graf med bådas positioner som funktion av tid.
Pieter Kuiper skrev:SaS.. skrev:Jag har ritat 3 olika situationer.
Innan, 10 sekunder efter och efter de 10 sekunderna har passerat.
Rita en graf med bådas positioner som funktion av tid.
När ska t=0 vara då? Innan eller efter?
SaS.. skrev:
När ska t=0 vara då? Innan eller efter?
Spelar väl ingen roll? Om det hände i morse klockan 8:00 eller 9:00?
Pieter Kuiper skrev:SaS.. skrev:
När ska t=0 vara då? Innan eller efter?Spelar väl ingen roll? Om det hände i morse klockan 8:00 eller 9:00?
Så kanske?
SaS.. skrev:Så kanske?
Nej. Gör det ordentligt: på rutpapper, med linjal, kvantitativt.
Eller med din grafritande räknare. Eller med Google.
Så kan du kolla om ditt resultat stämmer.
Pieter Kuiper skrev:SaS.. skrev:Så kanske?
Nej. Gör det ordentligt: på rutpapper, med linjal, kvantitativt.
Eller med din grafritande räknare. Eller med Google.
Så kan du kolla om ditt resultat stämmer.
Jag kan inte bestämma mina funktioner
SaS.. skrev:Föraren på ett tåg med hastigheten 117 km/h upptäcker ett stillastående lok 1200 m längre bort. Föraren börjar genast bromsa och signalerar samtidigt. 10 sekunder senare börjar äntligen loket att sätta sig i rörelse bort från tåget. Anta att de båda rörelserna är likformigt accelererade, och att tågets acceleration är -0,20 m/s2. Hur stor måste lokets acceleration minst vara för att enkollision skall undvikas?
Jag har ritat 3 olika situationer.
Innan, 10 sekunder efter och efter de 10 sekunderna har passerat.
Jag har kommit fram till en situation där jag har tåg A och tåg B.
Tåget A har en v=30.5m/s och a=-0.2m/s^2
Om jag plottar den funktionen i Google får jag:
https://www.google.com/search?q=y%3D30%2C5*t+-0%2C2*t%5E2/2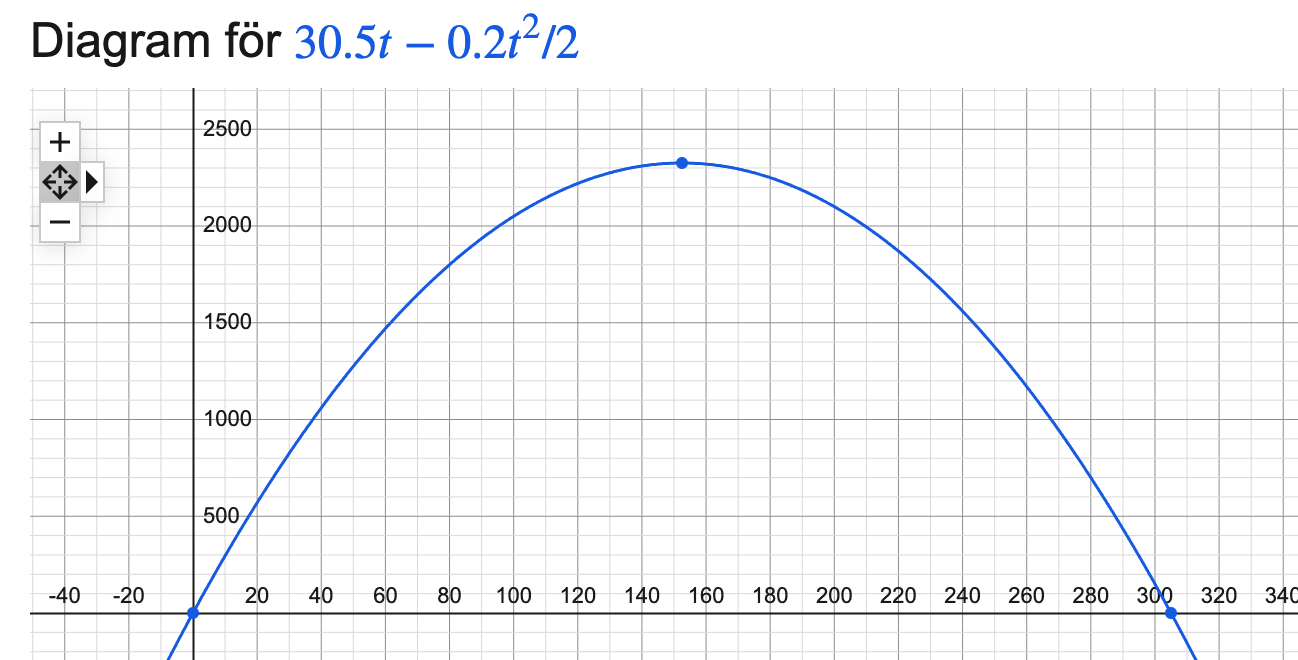 
Du kan lägga till funktionen för tåg B.
Pieter Kuiper skrev:SaS.. skrev:Föraren på ett tåg med hastigheten 117 km/h upptäcker ett stillastående lok 1200 m längre bort. Föraren börjar genast bromsa och signalerar samtidigt. 10 sekunder senare börjar äntligen loket att sätta sig i rörelse bort från tåget. Anta att de båda rörelserna är likformigt accelererade, och att tågets acceleration är -0,20 m/s2. Hur stor måste lokets acceleration minst vara för att enkollision skall undvikas?
Jag har ritat 3 olika situationer.
Innan, 10 sekunder efter och efter de 10 sekunderna har passerat.
Jag har kommit fram till en situation där jag har tåg A och tåg B.
Tåget A har en v=30.5m/s och a=-0.2m/s^2
Om jag plottar den funktionen i Google får jag:
https://www.google.com/search?q=y%3D30%2C5*t+-0%2C2*t%5E2/2Du kan lägga till funktionen för tåg B.
Jag får detta om accelerationen för tåget B är a= 0.74
SaS.. skrev:
Nej, tåget B står på 1200 meter vid t=10s.
Pieter Kuiper skrev:SaS.. skrev:Nej, tåget B står på 1200 meter vid t=10s.
Så du ser att kurvorna inte nuddar varandra. Tåget B hade kunnat accelerera mindre fort.
Pieter Kuiper skrev:Så du ser att kurvorna inte nuddar varandra. Tåget B hade kunnat accelerera mindre fort.
Ja precis, men hur gör jag nu? Kan man lösa det grafiskt?
Jag får inget annat svar algebraiskt
Ja precis, men hur gör jag nu? Kan man lösa det grafiskt?
Jag får inget annat svar algebraiskt
Du har just löst det grafiskt. Hur löser du det algebraiskt, menar du?
EDIT: Nej, du har inte löst uppgiften, du behöver variera a så att kurvorna precis nuddar varandra.
SaS.. skrev:Pieter Kuiper skrev:Så du ser att kurvorna inte nuddar varandra. Tåget B hade kunnat accelerera mindre fort.
Ja precis, men hur gör jag nu? Kan man lösa det grafiskt?
Jag får inget annat svar algebraiskt
Du kan testa dig fram.
Algebraiskt är det att likställa båda och hitta accelerationen som ger en och endast en lösning för t.
Smaragdalena skrev:Ja precis, men hur gör jag nu? Kan man lösa det grafiskt?
Jag får inget annat svar algebraiskt
Du har just löst det grafiskt. Hur löser du det algebraiskt, menar du?
Pieter Kuiper skrev:SaS.. skrev:Pieter Kuiper skrev:Så du ser att kurvorna inte nuddar varandra. Tåget B hade kunnat accelerera mindre fort.
Ja precis, men hur gör jag nu? Kan man lösa det grafiskt?
Jag får inget annat svar algebraiskt
Du kan testa dig fram.
Algebraiskt är det att likställa båda och hitta accelerationen som ger en och endast en lösning.
Har försökt med olika värde på a och fick det bästa till ungefär 0.33 m/s^2
Men om jag får detta på ett prov. Kan man svara med att "Jag har testat och fick svaret till a0.33m/s^2"?
SaS.. skrev:
Men om jag får detta på ett prov. Kan man svara med att "Jag har testat och fick svaret till a0.33m/s^2"?
Jag skulle tycka att det var bra (med en figur).
Men även om en lärare kräver en algebraisk lösning, har du nu väl tillräckligt för att skriva ner rätt ekvation?
Pieter Kuiper skrev:SaS.. skrev:
Men om jag får detta på ett prov. Kan man svara med att "Jag har testat och fick svaret till a0.33m/s^2"?Jag skulle tycka att det var bra (med en figur).
Men även om en lärare kräver en algebraisk lösning, har du nu väl tillräckligt för att skriva ner rätt ekvation?
Inte riktigt, jag fattar inte varför får jag 0.74 även om jag ställer upp rätt ekvation
SaS.. skrev:Inte riktigt, jag fattar inte varför får jag 0.74 även om jag ställer upp rätt ekvation
Man kan konkludera att du inte har rätt ekvation.
Pieter Kuiper skrev:SaS.. skrev:Inte riktigt, jag fattar inte varför får jag 0.74 även om jag ställer upp rätt ekvation
Man kan konkludera att du inte har rätt ekvation.
Hur gör jag då :(
Om jag sätter funktionena lika med varadra där t=30 ( Det får jag om jag sätter g(x)=885, alltså hur lång tid tar det för tåg a att köra 885 m) så får jag svaret negativt!
du skulle kunna tänka att du överger lokets acceleration till tåget med motsatt riktning
Då får du "låtsas" att loket står still och beräkna vilken acceleration som krävs för att tåget ska ha hastighet = 0 efter att den förs 885 meter
SaS.. skrev:Pieter Kuiper skrev:SaS.. skrev:Inte riktigt, jag fattar inte varför får jag 0.74 även om jag ställer upp rätt ekvation
Man kan konkludera att du inte har rätt ekvation.
Hur gör jag då :(
Om jag sätter funktionena lika med varadra där t=30 ( Det får jag om jag sätter g(x)=885, alltså hur lång tid tar det för tåg a att köra 885 m) så får jag svaret negativt!
Du vet inte t, i förväg vet du inte när det inträffar.
Men du vet att det finns ett moment där det är på samma plats.
Så likställ funktionerna, det ger en kvadratisk ekvation för t. Och du vet att det finns endast en lösning, det ger dig nästa ekvation för den okända accelerationen.
Pieter Kuiper skrev:SaS.. skrev:Pieter Kuiper skrev:SaS.. skrev:Inte riktigt, jag fattar inte varför får jag 0.74 även om jag ställer upp rätt ekvation
Man kan konkludera att du inte har rätt ekvation.
Hur gör jag då :(
Om jag sätter funktionena lika med varadra där t=30 ( Det får jag om jag sätter g(x)=885, alltså hur lång tid tar det för tåg a att köra 885 m) så får jag svaret negativt!
Du vet inte t, i förväg vet du inte när det inträffar.
Men du vet att det finns ett moment där det är på samma plats.
Så likställ funktionerna, det ger en kvadratisk ekvation för t. Och du vet att det finns endast en lösning, det ger dig nästa ekvation för den okända accelerationen.
Men den andra funktionen kommen ändå innehålla ett a som jag inte har
spazzy036 skrev:du skulle kunna tänka att du överger lokets acceleration till tåget med motsatt riktning
Då får du "låtsas" att loket står still och beräkna vilken acceleration som krävs för att tåget ska ha hastighet = 0 efter att den förs 885 meter
Du är verkligen SMART!
SaS.. skrev:Pieter Kuiper skrev:Du vet inte t, i förväg vet du inte när det inträffar.
Men du vet att det finns ett moment där det är på samma plats.
Så likställ funktionerna, det ger en kvadratisk ekvation för t. Och du vet att det finns endast en lösning, det ger dig nästa ekvation för den okända accelerationen.Men den andra funktionen kommen ändå innehålla ett a som jag inte har
Så kan du bestämma a. Antar jag att det borde funka.
Pieter Kuiper skrev:SaS.. skrev:Pieter Kuiper skrev:Du vet inte t, i förväg vet du inte när det inträffar.
Men du vet att det finns ett moment där det är på samma plats.
Så likställ funktionerna, det ger en kvadratisk ekvation för t. Och du vet att det finns endast en lösning, det ger dig nästa ekvation för den okända accelerationen.Men den andra funktionen kommen ändå innehålla ett a som jag inte har
Så kan du bestämma a. Antar jag att det borde funka.
Ja, men det blir ekvation med 2 variabler, t och a
SaS.. skrev:Ja, men det blir ekvation med 2 variabler, t och a
Och jag tror att jag har förklarat hur man kan få a.
Pieter Kuiper skrev:SaS.. skrev:Ja, men det blir ekvation med 2 variabler, t och a
Och jag tror att jag har förklarat hur man kan få a.
Jag hängde tyvärr inte med. Du skrev följande "du vet att det finns ett moment där det är på samma plats.Så likställ funktionerna, det ger en kvadratisk ekvation för t. Och du vet att det finns endast en lösning, det ger dig nästa ekvation för den okända accelerationen. " Och jag förstår inte det. Har du möjligheten att förklara mer :)
SaS.. skrev:
Jag hängde tyvärr inte med. Du skrev följande "du vet att det finns ett moment där det är på samma plats.Så likställ funktionerna, det ger en kvadratisk ekvation för t. Och du vet att det finns endast en lösning, det ger dig nästa ekvation för den okända accelerationen. " Och jag förstår inte det. Har du möjligheten att förklara mer :)
Det förstår du nog om du börjar med första steget. För det är inte alls svårt eller så.
Och så vidare steg för steg.
Jan Ragnar skrev:
Men måste dessa tåg ha samma hastighet där vid 1200 meter? Varför?
Det som jag ser i den grafiska lösningen (med värdet för acceleration som @spazzy036 så elegant bestämde) är att tågen nuddar varandra vid t=68 sekunder och s = 1750 meter.
Edit: men om jag läser mera noga har du samma värde som spazzy.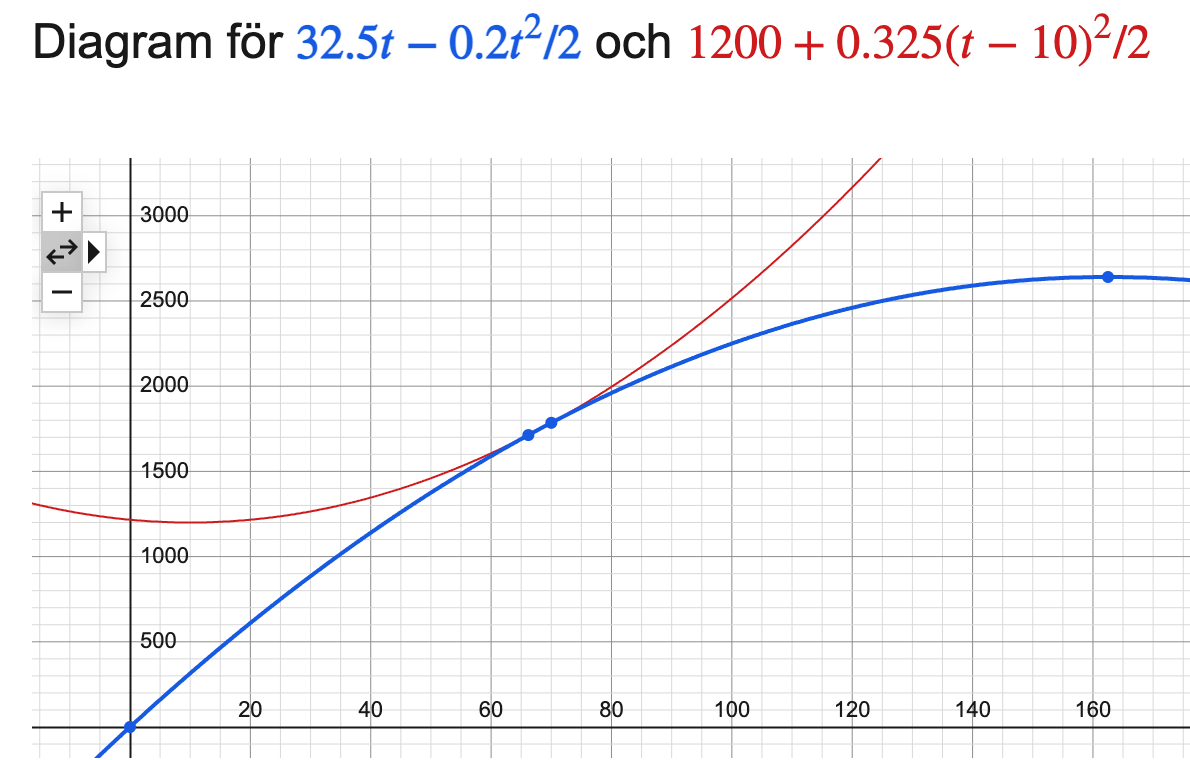
https://www.google.com/search?q=y%3D%2832%2C5*t+-0%2C2*t%5E2%2F2%29%2Cy%3D%281200%2B+0%2C325*%28t-10%29%5E2%2F2%29
När de båda tågen är så nära varandra som möjligt har de samma hastighet. Innan denna punkt blir av ståndet mindre och mindre, efter denna punkt blir avståndet större och större. Hela tiden gäller det ju att tåget bromsar och loket accelererar.
