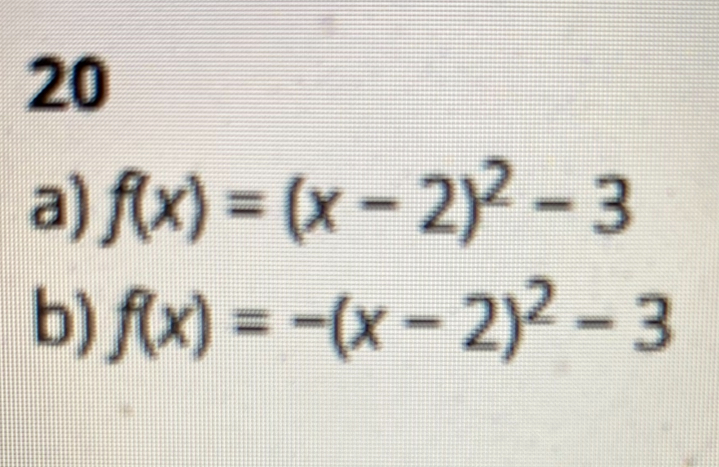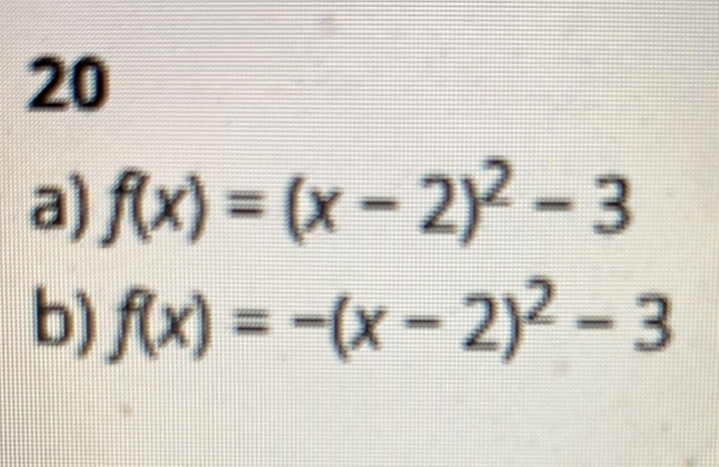Röd uppgift: Få fram en funktion med endast en punkt (Matematik/Matte 2)

Tänk på att det inte är vilken punkt som helst utan minimipunkten du fått reda på. Det är också viktigt att du förstår att det finns oändligt med funktioner som har en minimipunkt där och du behöver bara hitta en.

okej men hur går jag tillväga för att räkna fram en hel funktion utifrån endast en punkt?

Markera (2, -3) i ett koordinatsystem. Dra symmetrilinjen genom denna punkt. Kommer du vidare?

Hej, nej..
men, symmetrilinjen blir 2 om jag utgår från den punkten

Ja. Välj nu två nollställen som fungerar med denna symmetrilinje.

Okej, enklaste är (2,-3) och (2,0)

Tänkte f(x)= a (x-b)(x-c) men ser ett svar i facit som är mer lik f(x)= a(x-b)^2 + c.
Har inte gjort en sån här uppgift förr, och som sagt kan inte hitta någon genomgång eller förklaring på liknande uppgift..

Naturens skrev:
Okej, enklaste är (2,-3) och (2,0)

(2, -3) är inget nollställe.

(2, 0) kan inte ligga på grafen eftersom den pinkten är vertikalt rakt ovanför den givna punkten (2,-3).

Tänkte f(x)= a (x-b)(x-c) men ser ett svar i facit som är mer lik f(x)= a(x-b)^2 + c.

Din ansats går utmärkt även den.

Välj b och c så att de ligger på var sin sida om och lika långt från x = 2.

Nej sorry, du har rätt. Minimipunkten är (2,-3),
Så jag hittar den extrempunkten där x=2 och y=-3. Dock om jag ser svaret i facit så visas en funktion som har -2 (och -3), hur är räknestegen dit? och om det var tvärtom dvs att jag hade funktionen med extrempunkterna inskrivna redan, är meningen att jag ska räkna fram rent algebraiskt och visa hur -2 blir 2 liksom? eller är de något jag bara ska ha i huvudet?

Facit säger f(x) = (x − 2)² − 3 , så vill förstå vad formeln säger och betyder även om jag kanske kan gå runt de och lösa de på annat vis. Jag kan placera in punkten i denna formel, men vet inte hur jag ska räkna mig till det, eller hur jag ska använda formeln riktigt...

Så har läst och försökt förstå kvadratkomplettering formel alltså den här grejen: f(x)= a(x-x0)^2=y0.
Det står att denna formel ger funktionens extrempunkt direkt. Hur då ger? Hur räknar man sig dit? Jag placerar ju bara in punkten för jag har den redan liksom. Hur räknar jag fram extrempunkten genom denna formel?

Såg 2 exempeluppgifter så förstår vart jag ska skriva in min punkt i formeln. Men uppgifterna hade likt facit redan extrempunkterna placerade i formeln. Det fanns inget att räkna fram det var bara att ändra x-värdet i parentesen från ett negativt till ett positivt och så fick man svaret.

Vet inte vad a representerar rent grafiskt eller om jag ska räkna fram extrempunkten vad är det för värden från grafen som ska till a? vet bara att om den koefficienten a, är negativ så kan inte funktionen vara positiv dvs glad mun och sen tvärtom. Dvs negativ a ger positiv kurva, positiv a ger negativ kurva, eller då parabel.

I parentesen, alltså (x-x0)^2. så är x0 - extrempunktens värde på x axelns och Y0 - extrempunktens värde på y axelns.

Vet inte vad de andra x:et i parentesen ska representera grafiskt, vet bara att om jag vill få ett 0 där så tar jag det som redan står i den parentesen och sätter samma siffra fast ett + eller - ex (X-3) så (3-3)=0?

Men om jag tar facits svaret: f(x) = (x − 2)² − 3, så säger de här mig att:

-framför parentesen så är koefficienten positiv dvs +1 fast de inte står något där. Det betyder att parabeln är en glad mun, men som då har en minimipunkt.
- Ena x:et i parentesen, vet jag inte vad den ska representerar rent grafiskt, eller vad jag ska placera för värde där om jag ska räkna fram extrempunkten?
- De andra x:et som de nu står -2 på, är extrempunkten/minimipunkten 2 i uppgiften, men jag antar att den blir -2 i parentesen då formeln är -, dvs att +:et blir ett - bara för att formeln är liksom -. Antar också att om uppgiften hade ex -2 istället för +2, så skulle -x0 i parentesen och -2 som jag sätter in där, då blir ett + och då skulle svaret se typ ut så här: f(x) = (x + 2)² − 3 ?
- Den sista är -3 och det är y värdet på minimipunkten. Det är även denna siffra som står här som bestämmer vad funktionen har för största/minsta värde. Men igen om jag ska räkna fram vad x0 och y0 blir genom att ta hjälp av formeln så vet jag inte hur jag ska använda formeln.

Jag tänker på y= kx+m där jag vet att ex K är lutningen och m är skärningen med y axeln. Antar att denna formel kanske funkar lite på lika vis?, dvs att om jag har en parabel och jag ser värden på den parabeln genom axlarna, så ska jag kunna plocka ut de relevanta värden för parabeln och placera in de i formeln för att sen typ kunna räkna fram extrempunkten?

När Facit säger f(x) = (x − 2)² − 3, så förstår jag att jag ska placera ut punktens värden just där facit visar (visst är de så att +2 i uppgiften blir -2 för att formeln har ett -) men är osäker på hur jag räknar fram värdena med hjälp av formeln. De står i boken att "Varje andragradsfunktio kan uttryckas genom formeln" men visar inte riktigt hur man räknar, dom har bara placerat ut värden på formeln redan. Lika så exempeluppgifterna.

**Undrar också: om det står f(x) = (x − 2)² − 3, så betyder det att de framför parentesen (på a:s plats) står en osynlig +1 där. Betyder det då att f(x) = -(x − 2)² − 3, betyder att de står -1 där a egentligen skulle stå?

** En till grej, vart är a? varför är a inte med? är a automatiskt +1 /-1 ?

Naturens skrev:
Nej sorry, du har rätt. Minimipunkten är (2,-3),
Så jag hittar den extrempunkten där x=2 och y=-3. Dock om jag ser svaret i facit så visas en funktion som har -2 (och -3), hur är räknestegen dit?

Det beror på hur facit ser ut. Ladda gärna upp en bild.

och om det var tvärtom dvs att jag hade funktionen med extrempunkterna inskrivna redan, är meningen att jag ska räkna fram rent algebraiskt och visa hur -2 blir 2 liksom? eller är de något jag bara ska ha i huvudet?

Jag förstår intenriktigt vad du menar här.

En andragradsfunktion har endast en extrempunkt.

Facit säger f(x) = (x − 2)² − 3 , så vill förstå vad formeln säger och betyder även om jag kanske kan gå runt de och lösa de på annat vis. Jag kan placera in punkten i denna formel, men vet inte hur jag ska räkna mig till det, eller hur jag ska använda formeln riktigt...

Att f(x) = (x-2)²-3 säger oss följande:

Eftersom ett kvadratiskt uttryck aldrig är negativt så är funktionens minsta värde -3 och det inträffar när kvadraten är lika med 0, dvs då x = 2. Der ger oss direkt att funktionens minimipunkt är (2, -3).

Om du justerar formeln lite och sätter dit en positiv konstant k framför parentesen så blir uttrycket f(x) = k(x-2)²-3. Detta nya uttryck har precis som det tidigare (och av samma anledning som tidigare) en minimipunkt vid (2, -3). Det enda som skiljer är hur "djupt skålad" motsvarande parabel är.

Ju högre värde på k, desto "brantare" är parabeln.

Värdet på k påverkar även var nollställena hamnar.

Om k t.ex. är lika med 3 så får vi f(x) = 3(x-2)²-3 och nollställena hamnar då vid 3(x-2)²-3 = 0, dvs vid (x-2)² = 1, dvs vid x₁ = 1 och x₂ = 3.

Om k istället t.ex. är lika med 0,75 så får vi f(x) = 0,75(x-2)²-3 och nollställena hamnar då vid 0,75(x-2)²-3 = 0, dvs vid (x-2)² = 4, dvs vid x₁ = 0 och x₂ = 4.

Så har läst och försökt förstå kvadratkomplettering formel alltså den här grejen: f(x)= a(x-x0)^2=y0.
Det står att denna formel ger funktionens extrempunkt direkt. Hur då ger? Hur räknar man sig dit? Jag placerar ju bara in punkten för jag har den redan liksom. Hur räknar jag fram extrempunkten genom denna formel?

Jag förstår inte riktigt, kan du visa en bild?

Såg 2 exempeluppgifter så förstår vart jag ska skriva in min punkt i formeln. Men uppgifterna hade likt facit redan extrempunkterna placerade i formeln. Det fanns inget att räkna fram det var bara att ändra x-värdet i parentesen från ett negativt till ett positivt och så fick man svaret.

Vet inte vad a representerar rent grafiskt eller om jag ska räkna fram extrempunkten vad är det för värden från grafen som ska till a? vet bara att om den koefficienten a, är negativ så kan inte funktionen vara positiv dvs glad mun och sen tvärtom. Dvs negativ a ger positiv kurva, positiv a ger negativ kurva, eller då parabel.

I parentesen, alltså (x-x0)^2. så är x0 - extrempunktens värde på x axelns och Y0 - extrempunktens värde på y axelns.

Vet inte vad de andra x:et i parentesen ska representera grafiskt, vet bara att om jag vill få ett 0 där så tar jag det som redan står i den parentesen och sätter samma siffra fast ett + eller - ex (X-3) så (3-3)=0?

Men om jag tar facits svaret: f(x) = (x − 2)² − 3, så säger de här mig att:

-framför parentesen så är koefficienten positiv dvs +1 fast de inte står något där. Det betyder att parabeln är en glad mun, men som då har en minimipunkt.

Det stämmer. Bra!

- Ena x:et i parentesen, vet jag inte vad den ska representerar rent grafiskt, eller vad jag ska placera för värde där om jag ska räkna fram extrempunkten?

Se min förklaring ovan.

- De andra x:et som de nu står -2 på, är extrempunkten/minimipunkten 2 i uppgiften, men jag antar att den blir -2 i parentesen då formeln är -, dvs att +:et blir ett - bara för att formeln är liksom -. Antar också att om uppgiften hade ex -2 istället för +2, så skulle -x0 i parentesen och -2 som jag sätter in där, då blir ett + och då skulle svaret se typ ut så här: f(x) = (x + 2)² − 3 ?

Samma här, se min förklaring ovan.

- Den sista är -3 och det är y värdet på minimipunkten. Det är även denna siffra som står här som bestämmer vad funktionen har för största/minsta värde. Men igen om jag ska räkna fram vad x0 och y0 blir genom att ta hjälp av formeln så vet jag inte hur jag ska använda formeln.

Jag tänker på y= kx+m där jag vet att ex K är lutningen och m är skärningen med y axeln. Antar att denna formel kanske funkar lite på lika vis?, dvs att om jag har en parabel och jag ser värden på den parabeln genom axlarna, så ska jag kunna plocka ut de relevanta värden för parabeln och placera in de i formeln för att sen typ kunna räkna fram extrempunkten?

Det är inte lika tydlig koppling mellan konstanters värde och grafens utseende när det gäller andragradsfunktioner.

När Facit säger f(x) = (x − 2)² − 3, så förstår jag att jag ska placera ut punktens värden just där facit visar (visst är de så att +2 i uppgiften blir -2 för att formeln har ett -) men är osäker på hur jag räknar fram värdena med hjälp av formeln. De står i boken att "Varje andragradsfunktio kan uttryckas genom formeln" men visar inte riktigt hur man räknar, dom har bara placerat ut värden på formeln redan. Lika så exempeluppgifterna.

Hoppas jag har svarat på detta ovan?

**Undrar också: om det står f(x) = (x − 2)² − 3, så betyder det att de framför parentesen (på a:s plats) står en osynlig +1 där. Betyder det då att f(x) = -(x − 2)² − 3, betyder att de står -1 där a egentligen skulle stå?

Ja, det stämmer. Bra!

=======

Vi har ännu inte gått igenom de andra representationerna av andragradsfuntioner:

Faktoriserad form f(x) = k(x-x₁)(x-x₂)
Standardform f(x) = ax²+bx+c

Dessa två, tillsammans med den kvadratkompletterade formen de använder i facit, är bra på olika sätt:

Kvadratkompletterad form är bra om vi känner till extrempunktens koordinater.
Faktoriserad form är bra om vi känner till nollställena (vid x = x₁ och x = x₂)
Standardform är bra om vi känner till var parabeln skär y-axeln (vid y = c). övriga sammanhang

==========

Ställ gärna fler följdfrågor om det fortfarande är oklarheter kring detta.

Uppskattar hjälpen, tack, de vart lite fler frågor.

Numrerar det för enkelhetens skull:

1) Du skrev: (Eftersom ett kvadratiskt uttryck aldrig är negativt). Hur menar du, det står (x-2)^2 , det är negativt?

2)Du skrev: (funktionens minsta värde -3 och det inträffar när kvadraten är lika med 0, dvs då x = 2) Måste kvadraten alltså försvinna helt dvs bli =0, för att funktionen ska få sitt minsta/största värde? Kan man inte säga att funktionen har ett minsta/största värde trots att kvadraten finns kvar i uträkningen/formeln?

3)Du skrev: (funktionens minsta värde -3 och det inträffar när kvadraten är lika med 0, dvs då x = 2). Så det betyder att, de första X:et i kvadraten representerar den riktiga siffran för x-värdet, för just den punkten dvs 2, och eftersom att vi vet att 2 är det som får kvadraten att bli =0 så vet man automatiskt att punkten är (2,-3)? Medan de andra X:et representerar "tvärtom" siffran för x-värdet, för just den punkten dvs -2?

4) Jag uppskattar verkligen den här uträkningen du gjorde, tror jag förstår bättre när jag ser steg så här. Du skrev:

(Värdet på k påverkar även var nollställena hamnar. Om k t.ex. är lika med 3 så får vi f(x) = 3(x-2)2-3)

-Jag förstår det här steget.

(och nollställena hamnar då vid 3(x-2)2-3 = 0)

-Jag förstår detta steg, men vad menar du med att nollställerna hamnar då vid.. Vad representerar nollställen i detta? Vart ser du dom?

(, dvs vid (x-2)2 = 1, dvs vid x1 = 1 och x2 = 3.)

-Vet inte hur du räknar för att komma hit, det hoppar liksom fram fler steg som jag inte kan se i huvudet.

5)Uppgiften jag har är:

Facit är:

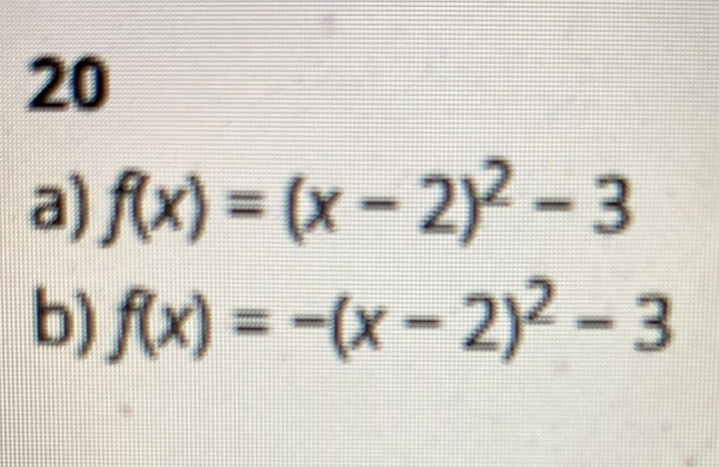
Fråga & ska försöka ställa den så bra jag kan: hur visar jag steg för steg i en uträkning med kvadratkompletterad form.

Hur jag får facit svaren. Tror inte det räcker med att jag vet vart jag ska placera punkten (2,-3) i formen utan behöver veta hur jag räknar?

Exempel på förvirring: vart försvinner a framför facit svaren/ parenteserna? Den måste ha ”räknats bort” i något räknesteg tänker jag?

Exempel på förvirring: vart kommer - framför facit svaret/parentesen i uppgift b) från, tänker att även den måste ha kommit till genom uträkning?

Naturens skrev:
Uppskattar hjälpen, tack, de vart lite fler frågor.

Numrerar det för enkelhetens skull:

1) Du skrev: (Eftersom ett kvadratiskt uttryck aldrig är negativt). Hur menar du, det står (x-2)^2 , det är negativt?

Nej, uttrycket (x-2) kan vara negativt, men kvadraten av detta, dvs (x-2)^2 år aldrig negativt.

Pröva själv med olika värden på x. Lyckas du få uttrycket stt bli negativt?

Naturens skrev:
Uppskattar hjälpen, tack, de vart lite fler frågor.

Numrerar det för enkelhetens skull:

1) Du skrev: (Eftersom ett kvadratiskt uttryck aldrig är negativt). Hur menar du, det står (x-2)^2 , det är negativt?

Nånting i kvadrat kan aldrig vara negativt (om nånting är ett reellt tal - om man börjar syssla med komplexa tal, som man läser i Ma4, så kan kvadrater vara negativa). Det betyder att vilket x-värde du än stoppar in så kan (x-2)² aldrig vara mindre än 0, och det är bara 0 om x = 2.

2)Du skrev: (funktionens minsta värde -3 och det inträffar när kvadraten är lika med 0, dvs då x = 2) Måste kvadraten alltså försvinna helt dvs bli =0, för att funktionen ska få sitt minsta/största värde? Kan man inte säga att funktionen har ett minsta/största värde trots att kvadraten finns kvar i uträkningen/formeln?

Funktionen har sitt minsta värde när parentesen som kvadreras har värdet 0 (eller största värde, om koefficienten för parentesen-i-kvadrat är negativ).

3)Du skrev: (funktionens minsta värde -3 och det inträffar när kvadraten är lika med 0, dvs då x = 2). Så det betyder att, de första X:et i kvadraten representerar den riktiga siffran för x-värdet, för just den punkten dvs 2, och eftersom att vi vet att 2 är det som får kvadraten att bli =0 så vet man automatiskt att punkten är (2,-3)? Medan de andra X:et representerar "tvärtom" siffran för x-värdet, för just den punkten dvs -2?

4) Jag uppskattar verkligen den här uträkningen du gjorde, tror jag förstår bättre när jag ser steg så här. Du skrev:

(Värdet på k påverkar även var nollställena hamnar. Om k t.ex. är lika med 3 så får vi f(x) = 3(x-2)2-3)

-Jag förstår det här steget.

(och nollställena hamnar då vid 3(x-2)2-3 = 0)

-Jag förstår detta steg, men vad menar du med att nollställerna hamnar då vid.. Vad representerar nollställen i detta? Vart ser du dom?

(, dvs vid (x-2)2 = 1, dvs vid x1 = 1 och x2 = 3.)

-Vet inte hur du räknar för att komma hit, det hoppar liksom fram fler steg som jag inte kan se i huvudet.

Det här är svårt att tyda eftersom det inte syns vad som är kvadrerat.

5)Uppgiften jag har är:

Facit är:

Fråga & ska försöka ställa den så bra jag kan: hur visar jag steg för steg i en uträkning med kvadratkompletterad form.

Hur jag får facit svaren. Tror inte det räcker med att jag vet vart jag ska placera punkten (2,-3) i formen utan behöver veta hur jag räknar?

Exempel på förvirring: vart försvinner a framför facit svaren/ parenteserna? Den måste ha ”räknats bort” i något räknesteg tänker jag?

Exempel på förvirring: vart kommer - framför facit svaret/parentesen i uppgift b) från, tänker att även den måste ha kommit till genom uträkning?

En andragradsfunktion har ett maximivärde om koefficienter n för kvadrattermen (när man skriver funktionen på formen y = ax²+bx+c) är negativ.

Naturens skrev:
2)Du skrev: (funktionens minsta värde -3 och det inträffar när kvadraten är lika med 0, dvs då x = 2) Måste kvadraten alltså försvinna helt dvs bli =0, för att funktionen ska få sitt minsta/största värde? Kan man inte säga att funktionen har ett minsta/största värde trots att kvadraten finns kvar i uträkningen/formeln?

Se tidigare svar. Om x har något annat värde än 2 så blir (x-2)^2 större än 0. Det blir då ett positivt tillskott till funktionsvärdet. Det betyder att om x har något annat värde än 3 så är funktionsvärdet större än -3.

För att funktionsvärdet ska bli så litet som möjligt måste alltså (x-2)^2 vara lika med 0

Naturens skrev:
[...]

3)Du skrev: (funktionens minsta värde -3 och det inträffar när kvadraten är lika med 0, dvs då x = 2). Så det betyder att, de första X:et i kvadraten representerar den riktiga siffran för x-värdet, för just den punkten dvs 2, och eftersom att vi vet att 2 är det som får kvadraten att bli =0 så vet man automatiskt att punkten är (2,-3)? Medan de andra X:et representerar "tvärtom" siffran för x-värdet, för just den punkten dvs -2?

Symbolen x i uttrycket betecknar det som kallas den oberoende variabeln (kallas ibland helt enkelt "variabeln")

Olika värden på detta x ger olika värden på uttrycket och därmed olika värden på funktionen.

Siffran 2 i uttrycket är inte "det andra x-et" utan helt enkelt ett tal.

Jämför en linjär funktion g(x) = 2x+5.

Här betecknar x (den oberoende) variabeln. Siffrorna 2 och 5 betecknar vanliga tal.

Beroende på vilket värde x har så får funktionen olika värden.

Om x t.ex. är lika med 1 så får funktionen värdet g(1) = 2*1+5 = 7.

Om x istället är 4 så får funktionen värdet g(4) = 2*4+5 = 13.

Naturens skrev:
[...]

4) Jag uppskattar verkligen den här uträkningen du gjorde, tror jag förstår bättre när jag ser steg så här. Du skrev:

(Värdet på k påverkar även var nollställena hamnar. Om k t.ex. är lika med 3 så får vi f(x) = 3(x-2)2-3)

-Jag förstår det här steget.

(och nollställena hamnar då vid 3(x-2)2-3 = 0)

-Jag förstår detta steg, men vad menar du med att nollställerna hamnar då vid.. Vad representerar nollställen i detta? Vart ser du dom?

Ett nollställe är en x-koordinat för vilket ett uttryck/funktion har värdet 0.

Exempel::

Funktionen g(x) = 2x+5 har ett nollställe där g(x) = 0, dvs där 2x+5 = 0, dvs där 2x = -5, dvs vid x = -5/2.

För funktionen f(x) = 3(x-2)^2-3 gäller det på samma sätt att nollställena ligger vid de x-koordinater där f(x) = 0, se nedan.

(, dvs vid (x-2)2 = 1, dvs vid x1 = 1 och x2 = 3.)

-Vet inte hur du räknar för att komma hit, det hoppar liksom fram fler steg som jag inte kan se i huvudet.

Vi har ekvationen

$3(x-2)^2-3 = 0$

Addera 3 till båda sidor och förenkla:

$3(x-2)^2 = 3$

Dividera båda sidor med 3 och förenkla:

$(x-2)^2=1$

Dra roten ur på båda sidor:

$x-2=\pm\sqrt{1}$

Förenkla:

$x-2=\pm1$

Dela upp i två fall:

Fall 1:

$x_1-2=-1$

Addera 2 till båda sidor.

$x_1=-1+2=1$

Fall 2:

x₂-2=1

Addera 2 till båda sidor:

$x_2=1+2=3$

Här är tre olika andragradsfunktioner som alla har ett minimum i punkten (2,-3):

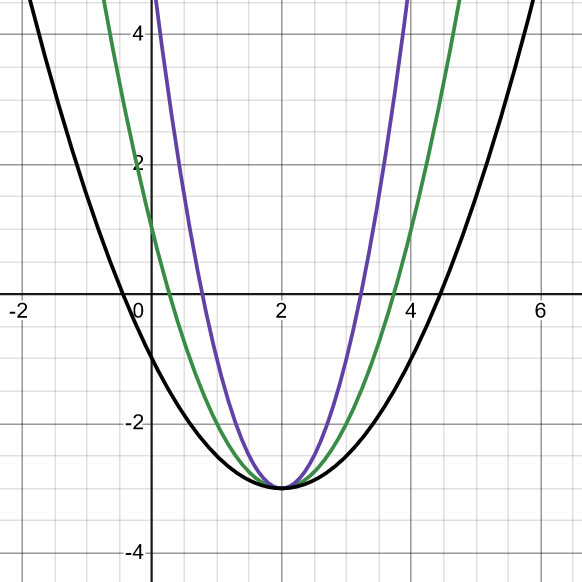
De kan alla beskrivas som f(x) = k(x-2)²-3 men k-värdena är olika - den svarta har k-värdet 0,5, den gröna 1 och den blålila 2.

Naturens skrev:
[...]

5)Uppgiften jag har är:

Facit är:

Fråga & ska försöka ställa den så bra jag kan: hur visar jag steg för steg i en uträkning med kvadratkompletterad form.

Hur jag får facit svaren. Tror inte det räcker med att jag vet vart jag ska placera punkten (2,-3) i formen utan behöver veta hur jag räknar?

Se tidigare svar: Att extrempunkten ligger vid (2, -3) innebär att den generella funktionen kan skrivas på kvadratkompletterad form enligt f(x) = a(x-2)^2-3.

Om a > 0 så får vi en "glad mun" med en minimipunkt.

Om a < 0 så får vi en "ledsen mun" med en maximipunkt.

Eftersom det endast efterfrågas en funktion som har de egenskaperna så kan vi fritt välja värde på a (då länge det är positivt eller negativt).

De har valt a = 1 för enkelhets skull.

Exempel på förvirring: vart försvinner a framför facit svaren/ parenteserna? Den måste ha ”räknats bort” i något räknesteg tänker jag?

De använder a = 1 i ena fallet och a = -1 i andra fallet

Exempel på förvirring: vart kommer - framför facit svaret/parentesen i uppgift b) från, tänker att även den måste ha kommit till genom uträkning?

Minustecknet behövs för att parabeln ska bli en "ledsen mun". Det måste nämligen vara så för att det ska finnas en maximipunkt.

Nu tror jag att jag har besvarat alla dina frågor.

Jag hoppas att det inte blev förvirrande för dig att vi var två personer som svarade mer eller mindre samtidigt här?

Fortsätt gärna att ställa följdfrågor, men ta då en fråga i taget för enkelhetens skull.

Tack. Okej.

Eftersom att det är en minimipunkt jag söker i A uppgiften betyder det att jag i förväg måste veta att värdet jag väljer på A måste vara positiv, för att ett positivt värde på A ger mig en minimipunkt. (Glad mun)?

vilket då betyder att värdet jag väljer i B uppgiften måste vara ett negativt värde då ett negativt värde på B ger mig en maximipunkt. (Ledsen mun)?

vad betyder/står ringarna/nollorna för i kvadratkompletterad form?

Jag gjorde A uppgiften & fick ut rätt svar enligt facit. Jag gjorde så här:

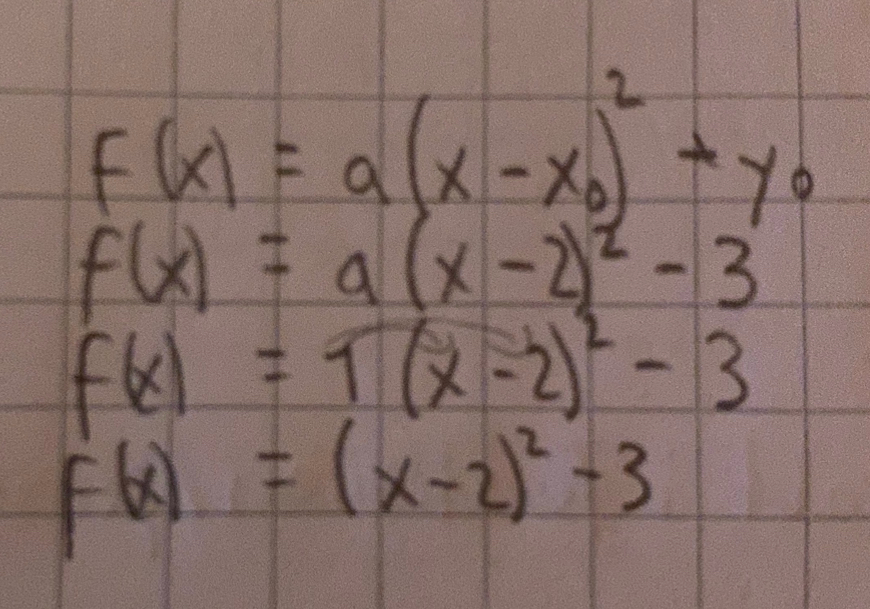
när jag försökte göra lika på B uppgiften vart det fel, det vart så här: (sluta räkna när jag såg att svaret vart fel, vet att -x ^2 inte är ok)

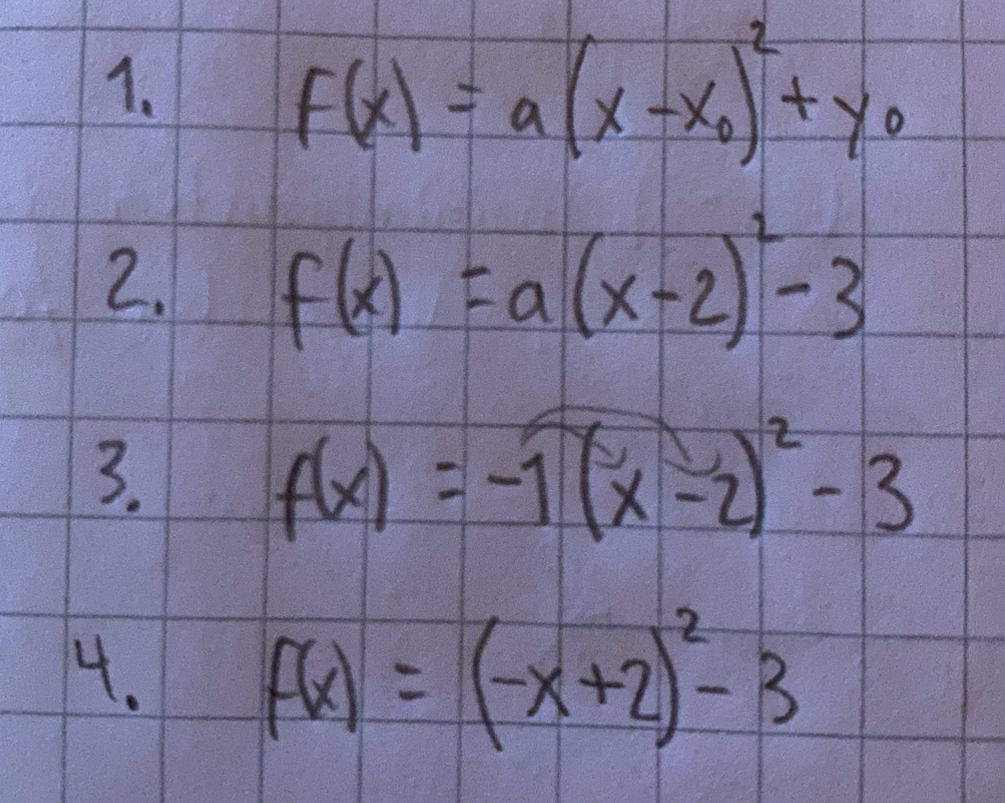
1. antar att jag inte ska räkna ut det, utan bara placera in punkten (2,-3) i formen?

2. vidare antar jag att det är A värdet i formen som bestämmer om parabeln får en maximipunkt eller en minimipunkt och detta genom att bara placera ut värdet +1/-1 framför parentesen & faktiskt inte räkna fram det, för de blir inte rätt på B uppgiften?

Steg 4 är inte rätt. Tänk på att

$- 1 {(x - 2)}^{2} - 3 = - 1 (x - 2) (x - 2) - 3$

Du har multiplicerat in -1 i båda parenteserna. Det enklaste är antagligen att räkna ut ${(x - 2)}^{2}$ och sen multiplicera det med -1. Så kan du använda andra kvadreringsregeln som genväg istället för vanlig parentesmultiplikation.

Naturens skrev:
Tack. Okej.

Eftersom att det är en minimipunkt jag söker i A uppgiften betyder det att jag i förväg måste veta att värdet jag väljer på A måste vara positiv, för att ett positivt värde på A ger mig en minimipunkt. (Glad mun)?

Ja, det stämmer.

vilket då betyder att värdet jag väljer i B uppgiften måste vara ett negativt värde då ett negativt värde på B ger mig en maximipunkt. (Ledsen mun)?

Ja, det stämmer.

Naturens skrev:
vad betyder/står ringarna/nollorna för i kvadratkompletterad form?

Det är nollor och de avser extrempunktens koordinater (x₀. y₀).

Vi kan lika gärna kalla extrempunktens koordinater (x₁, y₁), vilket ger oss f(x).= a*(x-x₁)^2-y₁.

Tackar mycket för all hjälp & tålamod!

Förstår inte riktigt hur du menar? för jag får inte svaret att bli -(x-2)^2 -3, med hjälp av räkning...
Har försökt få -1(x-2)^2 -3, till bara -(x-2)^2 -3 genom att räkna fram det svaret, alltså räkning stegvis och inte bara placera ett - framför parentesen. Men de går inte för mig. Det är typ omöjligt tror jag!
För jag gav upp efter ett tag & testa att scanna in -1(x-2)^2 -3 i en app som räknar ut utryck på olika vis steg för steg så man liksom kan se stegen & förstå vart man själv typ gjort fel/tänker fel, appen ger olika förslag på hur man kan räkna & visar stegen, men den appen gav inte heller ut ett svar som ger: -(x-2)^2 -3 =/

Vilken app var det? Exakt vad matade du in?

Den heter: Photomath

***
Jag skrev -1(x-2)^2 -3 på ett papper och scanna in den i appen & så får man olika förslag via appen.
Jag får inte fram något som leder till ett svar som ger -(x-2)^2-3.

Naturens skrev:
Den heter: Photomath

***
Jag skrev -1(x-2)^2 -3 på ett papper och scanna in den i appen & så får man olika förslag via appen.
Jag får inte fram något som leder till ett svar som ger -(x-2)^2-3.

Visa exakt hur papperet ser ut och vilka förslag appen gav.

Vad jag scanna in:

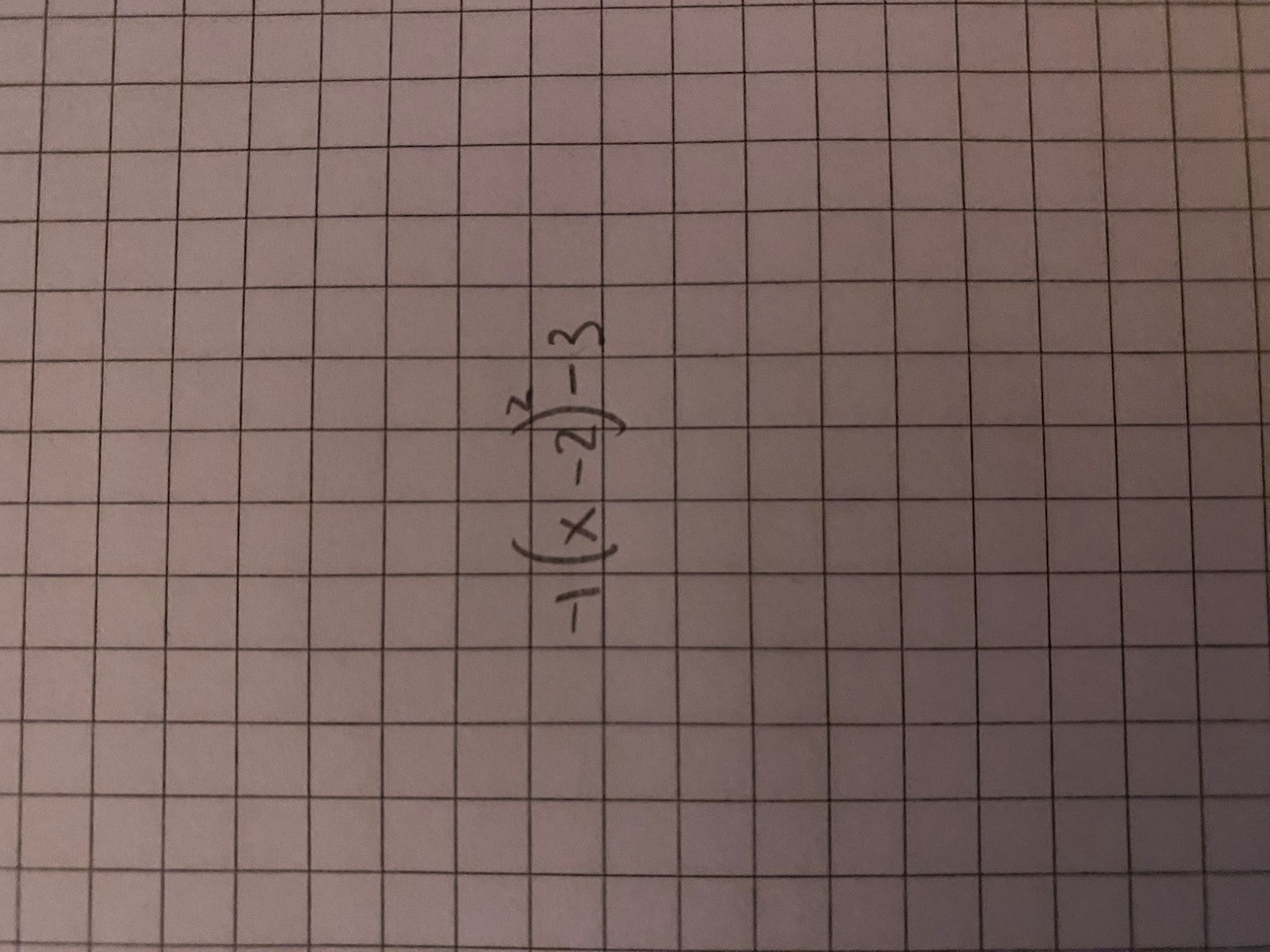
Lösningar appen ger:

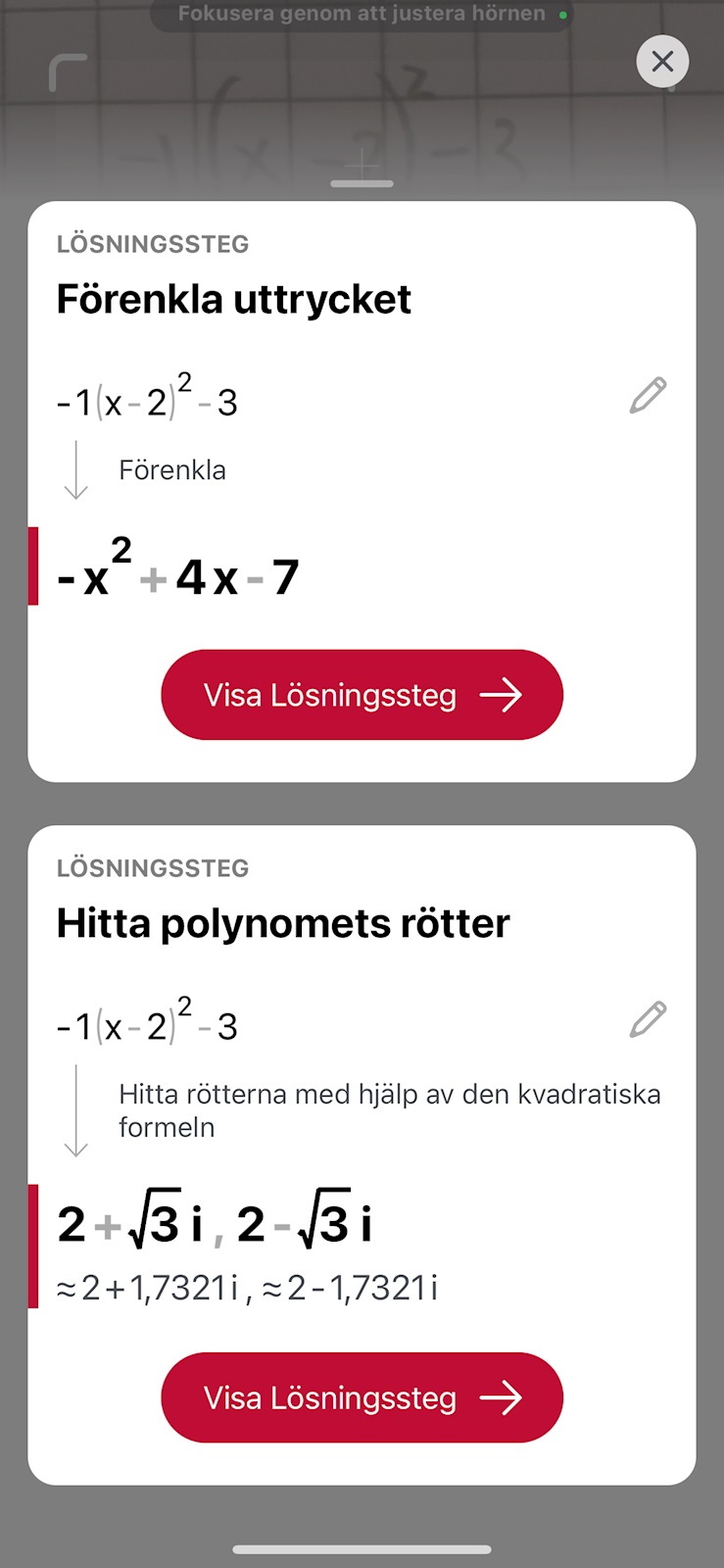
Allt som står i appen stämmer.

Men uppgifr 20 b gäller att ge ett exempel på en funktion som har en maximipunkt vid (2, -3).

Det som står i facut, nämligen $f(x) = -(x-2)^2-3$ , är ett exempel på ett sådant uttryck.

Grafen till $y=-(x-2)^2-3$ ser ut sp här:

Vi ser att den uppfyller villkoret i uppgiften eftersom den har en maximipunkt vid (2, -3).

Vad är det du vill att appen ska hjälpa dig med?

Tack.
Jag vill kunna räkna mig till svaret som facit visar. Precis som jag gjorde med a uppgiften. Dvs hur går jag från:

-1(x-2)^2 -3 till svaret, dvs -(x-2)^2 - 3 alltså stegen.

hur räknar jag fram de, går det?

***
Jag vet att
-(x-2)^2-3 är samma som -1(x-2)^2-3, men min tanke här är liksom,
om jag lär mig att räkna fram detta, dvs få bort siffran 1 framför parentesen,
så spelar de ingen roll vad som står på (a) platsen dvs -1 plats, för jag kan räkna fram det.

Hur gör man för att få bort siffran 1, hur får man -1(x-2)^2 - 3 att bli -(x-2)^2 - 3.
Eller är tanken här bara att jag ska tänka att,

Om uppgiften söker en maximipunkt, så placerar jag bara ut koordinaterna för maximipunkten i kvadratkompletterad form utan att försöka visa läraren hur jag räkna bort 1:an framför parentesen.
dvs
Jag skulle kunna lämna uppgiften så här:

Svar:
1(x-2)^2 - 3 Istället för (x-2)^2 - 3
-1(x-2)^2 - 3 Istället för -(x-2)^2 - 3

Vidare om jag har en punkt som kanske är (29,-65), så skulle minimipunkt/maximipunkt i funktion se ut så här:
1(x-29)^2 -65. eller. (x-29)^2-65
-1(x-29)^2-65 eller -(x-29)^2-65

Tänker jag rätt?

Naturens skrev:
Tack.
Jag vill kunna räkna mig till svaret som facit visar. Precis som jag gjorde med a uppgiften. Dvs hur går jag från:

-1(x-2)^2 -3 till svaret, dvs -(x-2)^2 - 3 alltså stegen.

hur räknar jag fram de, går det?

På samma sätt som en faktor 1 kan utelämnas så kn en faktor -1 ersättas av endast ett minustecken.

Exempel:

I uttrycket 1*a kan faktorn 1 utelämnas och uttrycket kan istället skrivas bara a

I uttrycket (-1)*a kan faktorn -1 ersättas av ett likhetstecken och uttrycket kan istället skrivas bara -a.

Med det sagt så är (-1)*(x-2)^2-3 ett helt korrekt svar, du behöver inte skriva om det.

Okej,

så då skulle detta också vara rätt om jag hade denna punkt:

En punkt som kanske är (29,-65), så skulle minimipunkt/maximipunkt i funktion se ut så här:
1(x-29)^2 -65. eller (x-29)^2-65
-1(x-29)^2-65 eller -(x-29)^2-65

P.S- Fråga angående din parabel som du skicka:
Vet du att parabeln skär y axeln vid -7, för att du fick fram den genom att räkna ut funktionen
(x-2)^2-3 till -x^2-4x-7 (en -7 som sen blir +7, när man tar -x^2*-1, för att få den x^2, men att man får tänka tvärtom dvs att det ska vara -7 parabeln skär och inte +7 då parabeln ska vara en minimipunkt)

Helt rätt. Utmärkt!

Tänk på att faktorn framför det kvadratiska uttrycket inte behöver vara just 1 för en minimipunkt, den kan vara vilket positivt tal som helst, t.ex. 0,23 eller 4711.

På samma sätt, för en maximipunkt kan faktorn vara vilket negativt tal som helst.

TACK SÅ MYCKET!!

skissar in punkterna i ett system bara för kul/ förstå bättre..
vet inte om du såg detta, men sista frågan på de här (lovar : )

P.S- Fråga angående din parabel som du skicka:Vet du att parabeln skär y axeln vid -7, för att du fick fram den genom att räkna ut funktionen-(x-2)^2-3 till -x^2-4x-7 (en -7 som sen blir +7, när man tar -x^2*-1, för att få bort - framför x^2, men att man då får tänka tvärtom dvs att det ska vara -7 )

Naturens skrev:
TACK SÅ MYCKET!!

skissar in punkterna i ett system bara för kul/ förstå bättre..
vet inte om du såg detta, men sista frågan på de här (lovar : )

Oroa dig inte, det finns ingen övre gräns för antalet frågor man får ställa, fråga bara på så mycket du vill. Vi tycker att det är bra med många frågor 👍

P.S- Fråga angående din parabel som du skicka:Vet du att parabeln skär y axeln vid -7, för att du fick fram den genom att räkna ut funktionen-(x-2)^2-3 till -x^2-4x-7 (en -7 som sen blir +7, när man tar -x^2*-1, för att få bort - framför x^2, men att man då får tänka tvärtom dvs att det ska vara -7 )

Nej, jag använde bara en gratis onlinetjänst som heter Desmos för att rita grafen, så jag tog inte ens reda på var grafen skär y-axeln.

Men du har rätt I att om vi skriver om funktionsuttrycket på standardform f(x) = ax²+bx+c (se svar #10) enligt f(x) = -(x-2)²-3 = -(x²-4x+4)-3 = -x²+4x-4-3 = -x²+4x-7 så ser vi direkt att c = -7 och att grafen alltså skär y-axeln vid y = -7.

En annan intressant spaning med standardform är att symmetrilinjen alltid ligger vid x = -b/(2a).

I det här fallet är a = -1 och b = 4, vilket ger att symmetrilinjen är x = -4/(2*(-1)) = -4/-2 = 2.

Har fått så bra hjälp här, TACK!!

Vad bra! Varsågod!