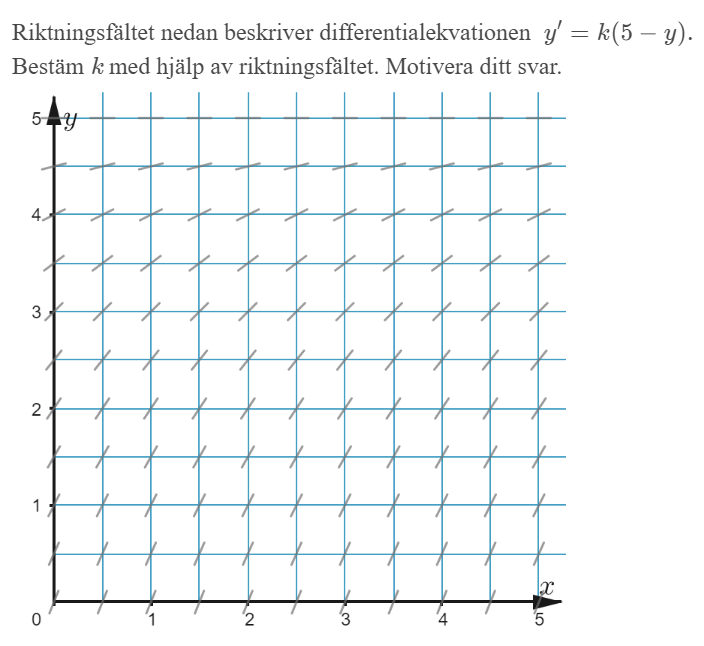
Riktningsfältet nedan beskriver differentialekvationen
Hej, jag förstår inte hur man ska lösa den här frågan. Bild två är på facit men jag förstår inte riktigt vad man ska göra i GeoGebra? Ska man testa olika värden på k? Hur vet man om man har rätt k-värde?
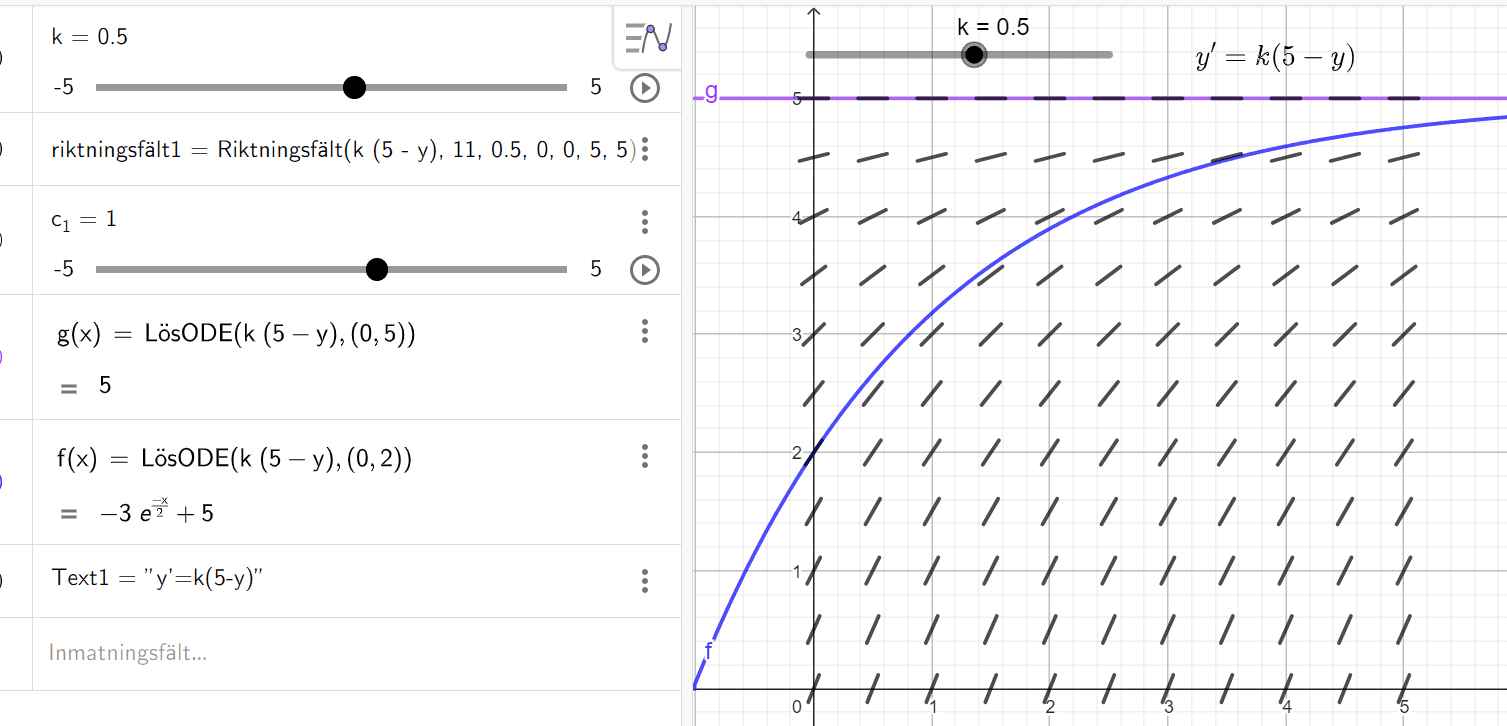
Lösningen är
Plotta 5 kurvor för lämpliga värden på .
Dra i reglaget för tills du hittar ett k-värde där _alla_ dina kurvor matchar riktningsfältet.
y' verkar vara 1 för y = 3.
D4NIEL skrev:Lösningen är
Plotta 5 kurvor för lämpliga värden på .
Dra i reglaget för tills du hittar ett k-värde där _alla_ dina kurvor matchar riktningsfältet.
Fast linjerna i riktningsfältet är väldigt korta och täta när jag skriver dem i GeoGebra, så jag vet inte riktigt ens hur jag ska jämföra dem.
Laguna skrev:y' verkar vara 1 för y = 3.
Jag testade att lösa på det här sättet algebraisk också men fick inte ut några värden, men det kanske var fel på uträkningen då.
Plotta fem kurvor, för , dra i reglaget runt
Kan du hitta ett värde på där kurvorna verkar matcha fältet?
Ska jag sätta olika c-värden och sedan testa olika k-värden för varje c-värde?
Uppgiften går ut på att du ska lära känna Geogebra samtidigt som du får en förståelse för hur lösningsskaran till en differentialekvation fungerar.
Differentialekvationen har lösningsskaran
Din uppgift är att klura ut vilket värde på som gör att lutningarna för lösningsskarans kurvor ungefär efterliknar riktningsfältet.
Här nedan är några lösningar till differentialekvationen plottade i diagrammet. Jag valde i mitt program (jag använder inte GeoGebra) och klistrade lite slarvigt in lösningarna över din bild:

Om du inte kan plotta flera lösningar räcker det med att du testar olika värden på för en lösning i taget. Varje lösning motsvarar ett värde på konstanten . Eftersom ekvationen saknar randvillkor är alla värden på egentligen tillåtna.
I facit har de valt att lösa ODEn för och , dvs de utgår från punkterna (0,2) samt (0,5). Men du får självklart även testa andra kurvor.
När blir ju lösningen
Så du ser direkt vilket värde på som motsvarar vilken kurva i facit. Om du till exempel vill ha den lila linjen i mitt diagram får du alltså lösa ekvationen för . Då misstänker jag att du kan skriva
h(x)=LösODE(k(5-y),(0,3))
Okej tack



