Riemansumma analystentafråga

Hej!
Jag vet inte var man ska börja på denna fråga. Hur bevisar man detta?
Formeln för en riemann sum är ju detta

Pröva att rita upp integralen, dela in den i rektanglar och försök tänka ut vad formeln för rektanglarna skulle vara.
Bedinsis skrev:Pröva att rita upp integralen, dela in den i rektanglar och försök tänka ut vad formeln för rektanglarna skulle vara.

Jag tänker delta x_k =b-a/n och i detta fall b=1 och a=0 så delta x_k=1/n. f(x_k)=(1/(1/n)+1)*(1/n)
Nej, ska vandra över intervallet, och bli större med ökande värden på k. Med ditt val blir oberoende av .
Ditt val ser dock bra ut.
D4NIEL skrev:Nej, ska vandra över intervallet, och bli större med ökande värden på k. Med ditt val blir oberoende av .
Ditt val ser dock bra ut.
Okej så hur ska jag bestämma f(x_k) och man får alltså inte multiplicera med delta x?
destiny99 skrev:D4NIEL skrev:Nej, ska vandra över intervallet, och bli större med ökande värden på k. Med ditt val blir oberoende av .
Ditt val ser dock bra ut.
Okej så hur ska jag bestämma f(x_k) och man får alltså inte multiplicera med delta x?
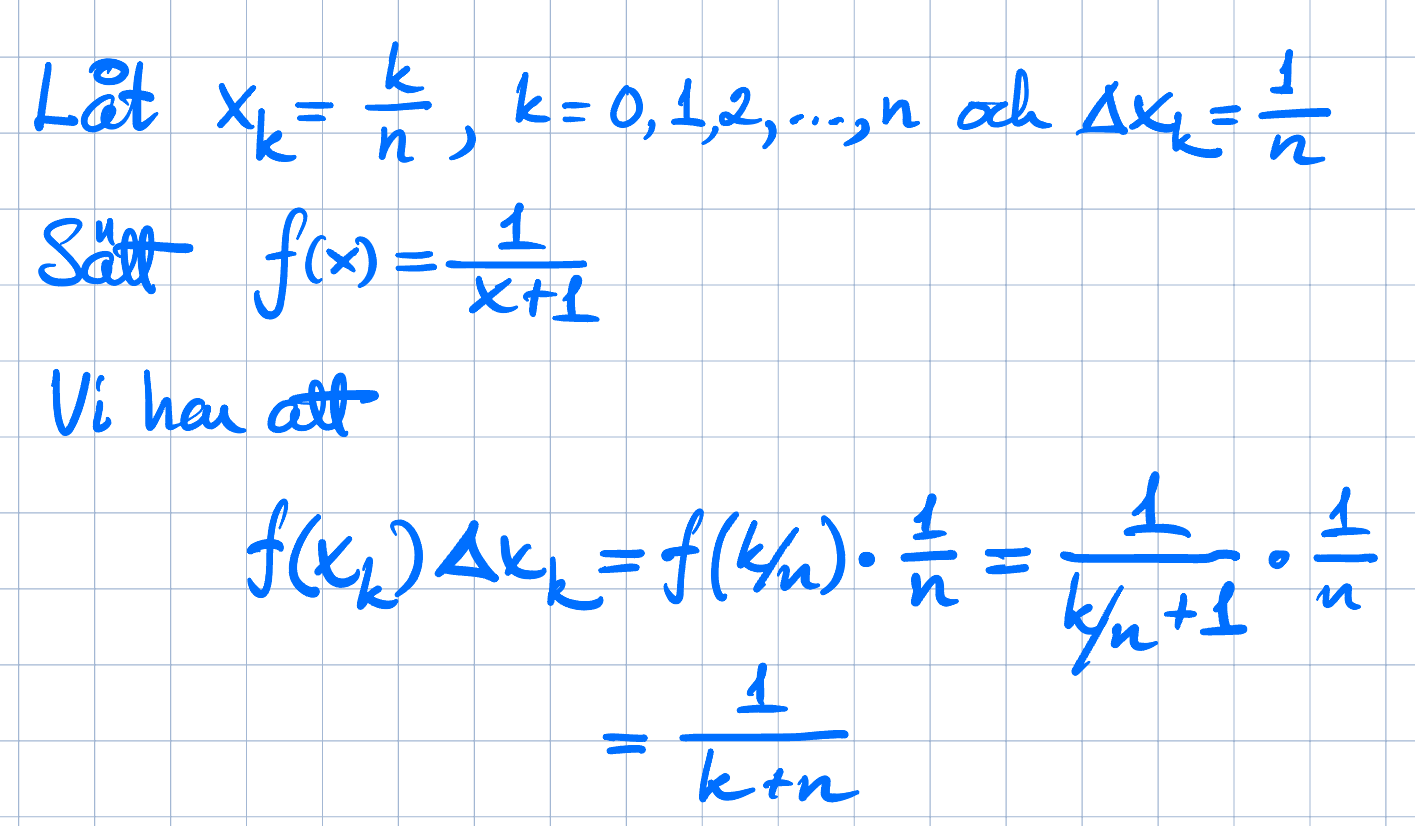
Trinity2 skrev:destiny99 skrev:D4NIEL skrev:Nej, ska vandra över intervallet, och bli större med ökande värden på k. Med ditt val blir oberoende av .
Ditt val ser dock bra ut.
Okej så hur ska jag bestämma f(x_k) och man får alltså inte multiplicera med delta x?
Ahaa det är så man ska göra. Ok nu har vi f(x_k)*delta x_k. Vi vet även att k börjar från 1 så det måste väl bli 1/(1+n)? Sen ska vi visa att a_n är en riemansumma till integralen, men jag antar att vi har gjort det då vi bestämt en riemansumma till integralen?
Ja, summan du ställt upp är per definition en Riemannsumma till integralen. Det finns också en sats som säger att om du låter antalet intervall, , gå mot oändligheten så har Riemannsumman gränsvärdet .
Lite mer exakt gäller om är kontinuerlig på , så finns till varje tal ett tal så att
För varje Riemannsumma med
När antar Riemannsumman den bestämda integralens värde. Nu kan du alltså beräkna den sökta summan genom att beräkna integralen istället.