Resonansfrekvens oscilloskop
Hej!
Jag kommer inte vidare till något svar på de här frågorna.

11) Vad jag har funderat på är att jag kanske kan koppla in en resistor, en induktans och en kapacitans i en krets med oscilloskopet. Om jag har värdena på resistorn, induktansen och kapacitansen och får värdet på spänningen borde jag kunna lösa ut och sen vidare lösa ut f. Jag kan inte komma på något annat tillvägagångssätt.
12) Att använda en voltmeter kanske? En voltmeter ger effektivvärdet på spänningen, till skillnad från oscillatorn som ger det faktiska värdet om jag har förstått det rätt.
11)
Gör som du föreslår, koppla en resistans, en induktans och en kapacitans i serie. Sen står det att du ska använda ett oscilloskop, inte räkna ut den.
När du har resonans, vad innebär det för spänningen över resistansen?
Och hur ser spänningen över och strömmen genom resistansen ut vid resonans? (Fasförskjutning?)
12)
Ett sätt är att mäta effektivvärdet på spänningen över och strömmen genom resistansen. Vad ska de bli om vi har resonans? Lite grann som andra metoden på 11:an.
11)
Att all spänning är över resistorn? Induktansen och kapacitansen tar ut varandra spänningsmässigt då deras spänningar är lika stora men motriktade.
Ingen fasförskjutning i en rent resistiv krets (vilket den upplevs som här om jag förstått det rätt).
12)
Att de ska vara proportionella mot varandra och R? Alltså U=RI igen?
Eller är det att effekten ska bli 1? Det finns trianglar för effekten med induktans och kapacitans vet jag, men när kretsen är i resonans borde dessa ta ut varandra tänker jag så att vinkeln ?
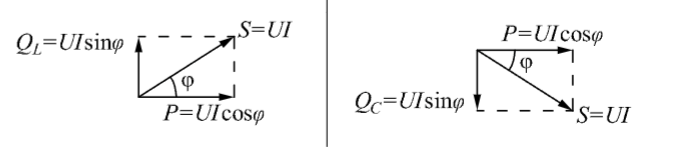
Just det, i en seriekrets får du maxspänning över resistansen och ström och spänning är i fas vid resonans.
Om man mäter effektivvärden så gäller U = RI bara om ström och spänning är i fas, som vid resonans. Har bara svårt att komma på ett sätt till.
Kom på ett sätt till. Det går ju också att mäta effektivvärdena av spänningarna över induktansen och kapacitansen. När de är lika har vi resonans.
Tack för hjälpen!


