Resistorer

Jag har ritat en bild.(Derödakrusedullernapåkanternaärresistorer) Den här tänkte jag att man skulle kunna rita såhär förenklat:
Den här tänkte jag att man skulle kunna rita såhär förenklat:

stämmer detta?
Nej. Du kan reagera på att att hörnen i din graf endast är kopplade till två resistorer men i en kub är varje nod kopplas till tre resistorer.
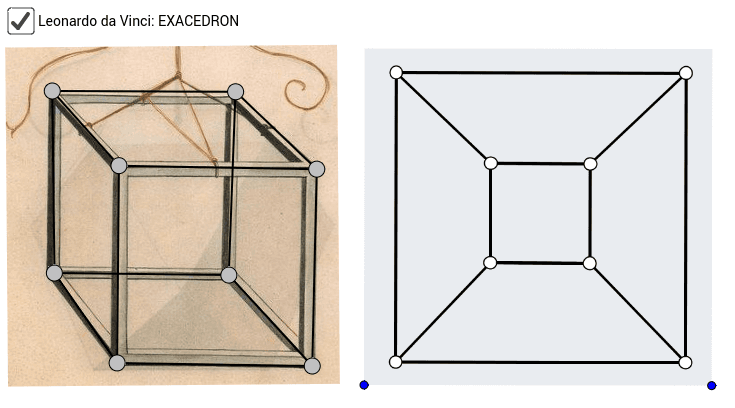
Om man plattar ut en kub så får man ovan bilder. Du kan komma fram till detta genom att tänka dig hur en genomskinlig kub ser ut om man betraktar den ovanifrån.
Vilken nivå läser du fysik på? Det underlättar för oss som svarar om vi vet om du går på högstadiet eller läser fysik på universitetet - vi formulerar oss olika i de båda fallen. Du kan själv flytta din tråd till rätt nivå genom att redigera ditt förstainlägg (inom 2 timmar). /moderator
Nej, det stämmer inte. Om du tänker dig kuben på högkant så kommer de 6 resistorerna som är "närmast ekvatorn" att ha samma potential, så där kommer det inte att gå någon ström. Du kan alltså tänka dig att du plockar bort dem utan att några strömmar eller spänningar förändras.
Ett klassiskt problem som är svårt till en början men ganska enkelt när man förstår vad man kan göra. Testa att använda Kirchoffs strömlag:
 Det kommer in en ström på 3 Ampere i ett av hörnen. Detta delas upp enligt Kirchoffs strömlag jämnt mellan varje av sidorna eftersom resistanserna i sidorna är lika. Vi får därmed 1 A av ström som flödar i sidorna enligt bilden. Detta resulterar i följande spänningsfall:
Det kommer in en ström på 3 Ampere i ett av hörnen. Detta delas upp enligt Kirchoffs strömlag jämnt mellan varje av sidorna eftersom resistanserna i sidorna är lika. Vi får därmed 1 A av ström som flödar i sidorna enligt bilden. Detta resulterar i följande spänningsfall:

Alltså att vi har ett spänningsfall på U = R·I = R Volt. Nu är det upp till dig att räkna ut spänningsfallet mellan två motsatta hörn och sedan dela detta med totala strömmen på 3 Ampere för att få ut den sökta resistansen.
Närmaste vägen mellan två motstående hörn passerar alltid tre resistorer.
Börja i punkten vi kallar "A" och antag att därifrån lämnar strömmen "3I".
Pga. symmetri lämnar strömmen "I" i var och en av de tre grenarna från punkten A.
Man tycks då kunna rita: Kommer du vidare?
Kommer du vidare?
Ebola skrev:Ett klassiskt problem som är svårt till en början men ganska enkelt när man förstår vad man kan göra. Testa att använda Kirchoffs strömlag:
Det kommer in en ström på 3 Ampere i ett av hörnen. Detta delas upp enligt Kirchoffs strömlag jämnt mellan varje av sidorna eftersom resistanserna i sidorna är lika. Vi får därmed 1 A av ström som flödar i sidorna enligt bilden. Detta resulterar i följande spänningsfall:
Alltså att vi har ett spänningsfall på U = R·I = R Volt. Nu är det upp till dig att räkna ut spänningsfallet mellan två motsatta hörn och sedan dela detta med totala strömmen på 3 Ampere för att få ut den sökta resistansen.
Tack för alla asgrymma svar. riktigt bra förklaring! blir det här rätt?:
Smaragdalena skrev:Vilken nivå läser du fysik på? Det underlättar för oss som svarar om vi vet om du går på högstadiet eller läser fysik på universitetet - vi formulerar oss olika i de båda fallen. Du kan själv flytta din tråd till rätt nivå genom att redigera ditt förstainlägg (inom 2 timmar). /moderator
Nej, det stämmer inte. Om du tänker dig kuben på högkant så kommer de 6 resistorerna som är "närmast ekvatorn" att ha samma potential, så där kommer det inte att gå någon ström. Du kan alltså tänka dig att du plockar bort dem utan att några strömmar eller spänningar förändras.
Okej! Det ska jag tänka på tills nästa gång. dock tycker jag det är lite svårt att sätta nivå på uppgifterna ifall jag gör något form av prov online. t.ex här matte o fysikprovet.
pepsi1968 skrev:Tack för alla asgrymma svar. riktigt bra förklaring! blir det här rätt?:
Tyvärr inte rätt.
Spänningsfallet mellan två motsatta hörn är som man kan se i din bild:
Om vi nu delar detta spänningsfall med totala strömmen får vi ut resistansen:
Nej, svaret på detta klassiska problem är att det blir som en parallellkoppling av 3 grenar som vardera innehåller 2 seriekopplade resistorer.
Smaragdalena skrev:Nej, svaret på detta klassiska problem är att det blir som en parallellkoppling av 3 grenar som vardera innehåller 2 seriekopplade resistorer.
Hur menar du att det blir det? Jag skulle säga en ekvivalent krets är:

Detta summeras till resistansen .
Jag skrev tidigare:
Om du tänker dig kuben på högkant så kommer de 6 resistorerna som är "närmast ekvatorn" att ha samma potential, så där kommer det inte att gå någon ström. Du kan alltså tänka dig att du plockar bort dem utan att några strömmar eller spänningar förändras.
Smaragdalena skrev:Jag skrev tidigare:
Om du tänker dig kuben på högkant så kommer de 6 resistorerna som är "närmast ekvatorn" att ha samma potential, så där kommer det inte att gå någon ström. Du kan alltså tänka dig att du plockar bort dem utan att några strömmar eller spänningar förändras.
Aha, fast det där förstår jag inte eftersom strömmen måste gå igenom dessa resistorer. Du kan inte kortsluta mellan två punkter med olika potential utan att påverka kretsen.
Vi tittar på kuben igen:

De blåröda noderna har samma potential så vi kan kortsluta mellan dem:
 Likaså har de rödgröna samma potential (inte samma som de blåröda!) så vi kan kortsluta mellan dem:
Likaså har de rödgröna samma potential (inte samma som de blåröda!) så vi kan kortsluta mellan dem: Den slutliga kretsen ser ut som följer:
Den slutliga kretsen ser ut som följer: Om du fortfarande inte tror mig kan du kolla upp huruvida jag har rätt eller ej här. Kolla under fråga 18.
Om du fortfarande inte tror mig kan du kolla upp huruvida jag har rätt eller ej här. Kolla under fråga 18.
Affe Jkpg skrev:Närmaste vägen mellan två motstående hörn passerar alltid tre resistorer.
Börja i punkten vi kallar "A" och antag att därifrån lämnar strömmen "3I".
Pga. symmetri lämnar strömmen "I" i var och en av de tre grenarna från punkten A.
Man tycks då kunna rita:Kommer du vidare?
I denna tråd förekommer diverse fantasifulla illustrationer :-)
Adderat till ovanstående illustration föredrar jag denna:

Man skulle även kunna ta Affes diagram och sedan räkna på effekt. Då kommer man runt parallell/serietänk och kan fokusera på att effekten som utvecklas i hela kretsen är summan av deleffekterna
där alltså är delströmmarna genom genom resistorer är och är andelen av matningsströmmen varifrån eesättnibgsresistansen blir






