Relativt prima tal med inklusion-exklusion

Det är för mig litet oklart om 1 ska anses ligga mellan 1 och n.

Jag låter 1 vara ett tal mellan 1 och n, så får vi dra bort ett från slutantalet.

I så fall börjar vi med n tal: 1, 2, 3, …, n.

Det finns n/p₁ tal av dessa  som är delbara med p₁. De ska bort. Kvar är n–n/p₁

Det finns n/p₂ tal som är delbara med p₂. De ska också bort. Kvar är n–n/p₁ –n/p₂

Men nu har vi dragit bort alla multipler av p₁p₂ två gånger, vi ska bara dra bort dem en gång. Så vi måste lägga till n/(p₁p₂). Kvar är …

Sedan drar vi bort alla som är delbara med p₃. Men vi måste lägga till antalet multipler av p₁p₃ och p₂p₃.

Och dra bort antalet multipler av p₁p₂p₃ ….

Jag testar med n = 90 = 2*3²*5

Det finns 45 jämna tal, Kvar 45.

Det finns 30 tal delbara med 3. Kvar 15.

Men det finns 15 tal delbara med 2*3. Lägg till, vi får 30

Det finns 18 tal delbara med 5. Ta bort. Kvar 12

Lägg till 9 tal delbara med 2*5. Kvar 21.

Lägg till 6 tal delbara med 3*5. Kvar 27

Dra bort 3 tal delbara med 2*3*5. Kvar 24.

Kolla: 1,7,11,  13,17,19,  23,29,31,  37,41,43,  47,49,53,  59,61, 67,  71,73,77, 79,83,89

Det blev 24, Men eventuellt ska ettan i början bort.

Det blir litet grötigt att skriva en allmän formel med många olika primtal i faktoriseringen av n. Men strukturen har jag sett i sannolikhetsläran. Sannolikheten för att A eller B eller C ska hända är
P(A) + P(B) +P(C) – P(A snitt B) – P(A snitt C) – P(B snitt C) + P(A snitt B snitt C). 
Det är väl det som termerna inklusion–exklusion avser?

(I sannolikhetsformeln blir tecknen omvända eftersom Övning 6 frågar hur många som är kvar. Hade vi i stället frågat hur många tal vi tar bort skulle vi fått samma tecken.)

Tänkte bara flika in att notationen $[n]$ betyder mängden $\{1,2,\dots,n\}$, så det är riktigt att talen 1 och $n$ ingår.

Det där lät som en bra strategi!

Om man utgår från det här teoremet om inklusion-exklusion, så kanske man kan uttrycka det med den här formeln:

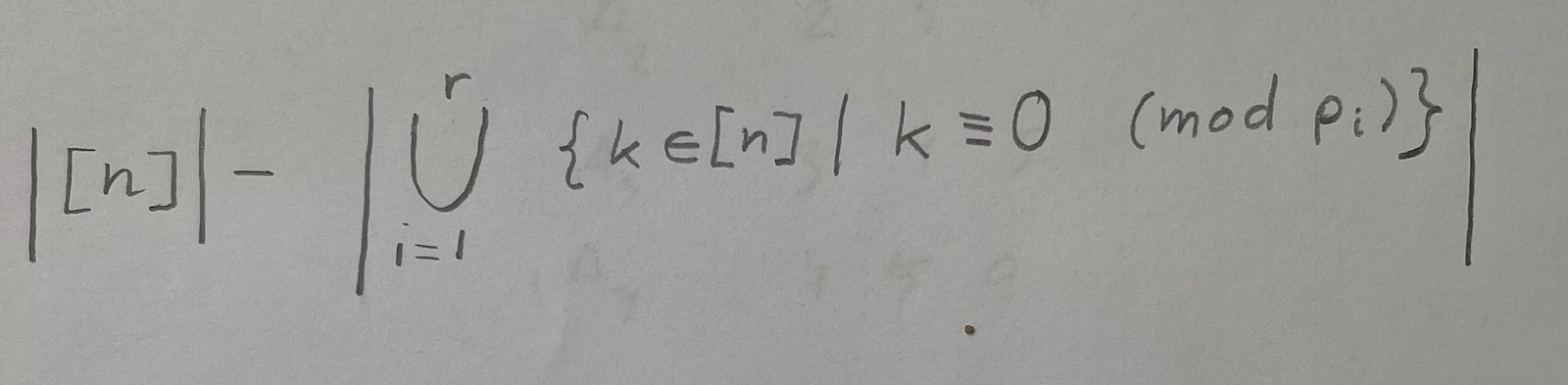
Jag tycker det ser väldigt proffsigt ut.

Tack 😃