Relativitet

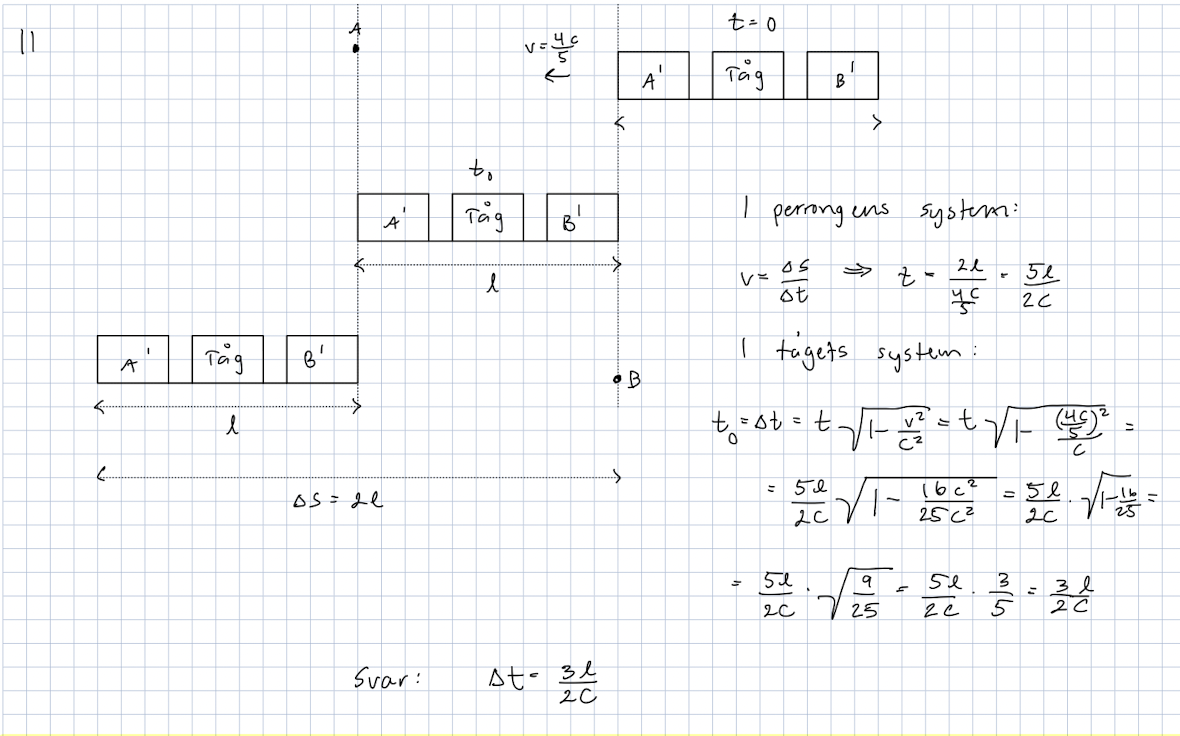
Hur långt är tåget i tågets system? Hur lång är perrongen i tågets system?

Hur långt ska perrongen alltså färdas?

Hur lång tid tar det?

Ingen aning.
Är tågets längd enligt tåget vilolängden? Visst ser perrongen ett kortare tåg?

Ja, perrongen ser kortare ut, närmare bestämt $l'=\frac{l_0}{\gamma}$

Jag förstår fortfarande inte vilken sträcka tåget ska åka. Jag lärde mig att vilolängden tillhör det system där vilolängden inte rör sig relativt det systemet. Sträckan tåget har rört sig rör sig ju inte relativt perrongen. Det är det enda jag kommer på.

Det står i frågan att vi skall räkna i tågets inertialsystem, d v s räkna med att tåget står stilla och resten av världen rör sig.

Problemformuleringen vill veta hur lång tid passagen tar i tågets system.

Därför kan det vara enklast att betrakta tåget som stillastående och perrongen som rör sig. Hur långt ska perrongen flytta sig enligt tåget?

I tågets system är tåget fortfarande $l$ långt. Däremot har perrongen blivit kortare, närmare bestämt $\frac{l}{\gamma}$.

Perrongen ska alltså färdas sträckan

$s=l(1+\frac{1}{\gamma})$

Hur lång tid tar det?

$t=\frac{s}{v}=\frac{l(1+\frac{1}{\gamma})}{\frac45c}$

Eftersom $\frac{1}{\gamma}=\frac35$ får vi

$t=\frac{l(1+\frac35)}{\frac45c}=\frac{2l}{c}$

Okej nu förstår jag. Tack så mycket!