Rekurrensekvation; ansats till den partikulära lösningen

En inhomogen rekurrensekvation löses genom att addera den homogena lösningen med den partikulära lösningen.
Homogena lösningen :
Den karakteristiska ekvationen är .
Med dessa kan vi skapa uttrycket för den allmänna homogena lösningen
Partikulära lösningen :
Vår ansats ska matcha den inohomogena delens polynomtal...
MEN!
[Här gör jag ett ekvationsystem för att räkna ut A och B, vilket kommer att slutföra den slutgiltiga ekvationen]
Polynomtalet för är ju inte bestämt, och jag vet inte hur man ansätter sådana. Jag hittade i en anteckning att detta kan ansättas med men jag förstår inte riktigt varför. Skulle någon kunna förklara varför det blir denna ansats?
Tack
Om xn är E 2n så blir xn+1 = E 2n+1 = 2E 2n och xn+2 = 4E 2n så vänsterledet blir ett uttryck i 2n som kan matchas mot högerledet.
Jag tänkte på talet e, men du menade en variabel E. Det stog dessutom c i lösningsförslaget, läste visst inte igenom ordentligt...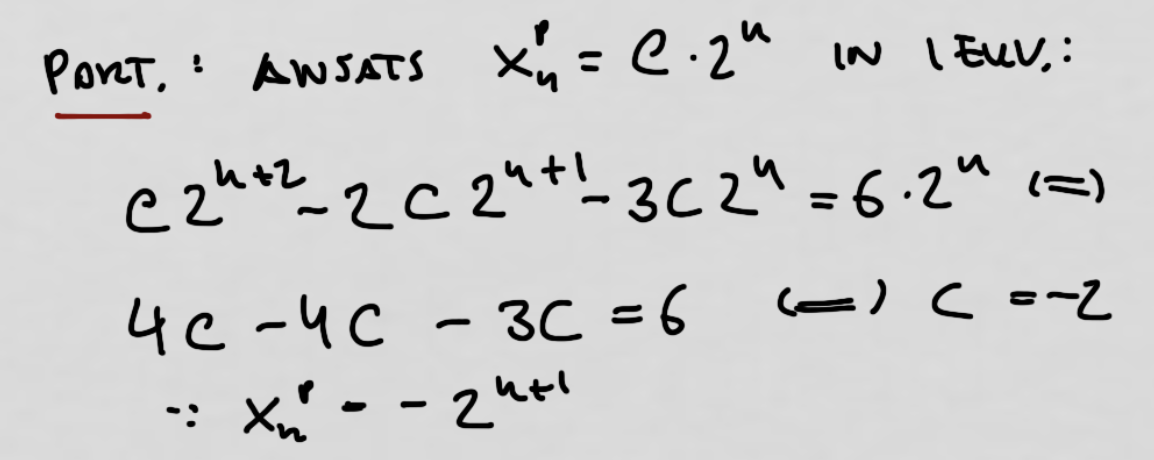 Ber om ursäkt för det... Tack för ditt svar ändå! :D
Ber om ursäkt för det... Tack för ditt svar ändå! :D
Inget att be om ursäkt för, situationen är väldigt lik den där man löser differentialekvationer, och där kommer e in. Lätt att trampa fel.


