Regler för bråk, förhållanden
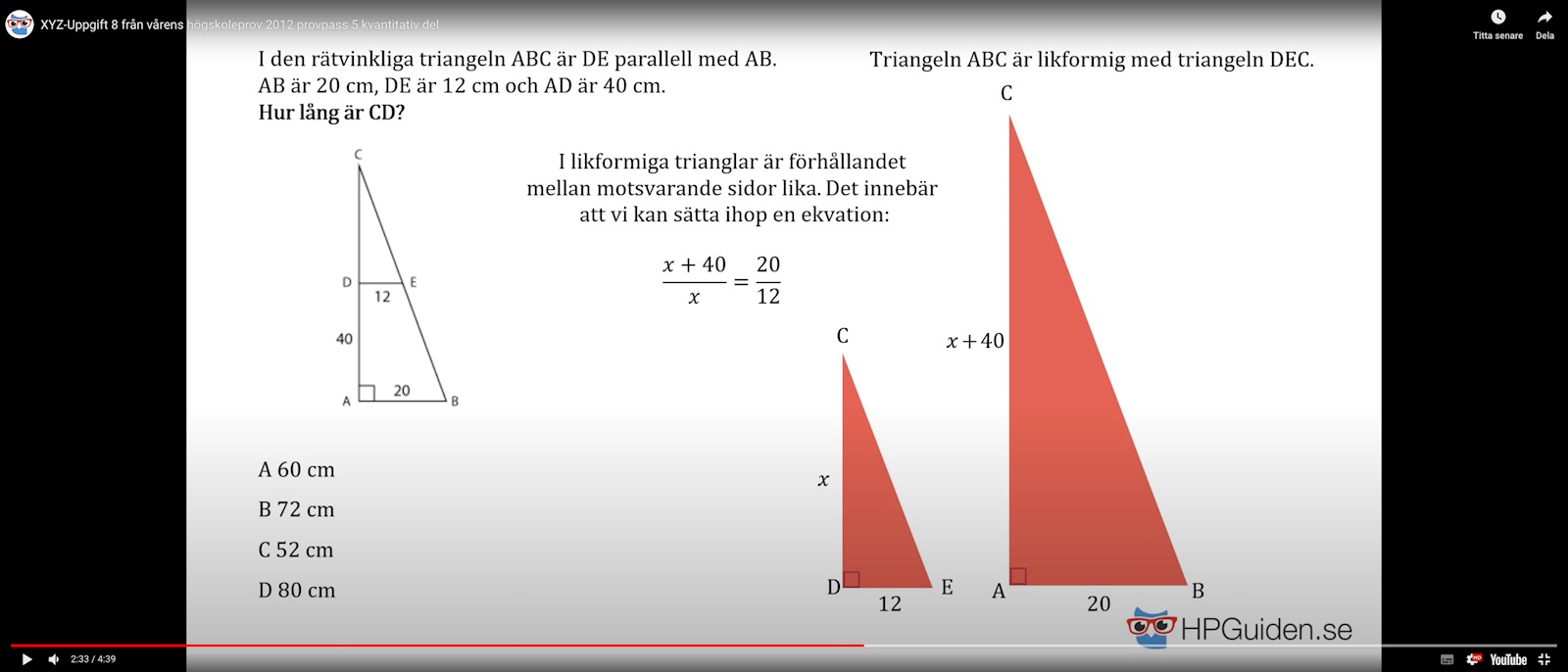Jag finner denna väldigt svår att lösa på 1 minut. Vilket jag såklart inte gjorde. En fråga är tar man alltid den större triangeln delat på den lilla när man ska ta ut förhållandet på likformiga trianglar eller kan man lika gärna ha
Vill väldigt gärna inte utelämna några regler för jag har gjort fel pga osäkerhet på vissa uppgifter när det kommer till just hur man får bearbeta bråk. De flesta kan jag som korsmultiplikation, invers vid division, förlängning osv men kommer ni på någon mer så är jag evigt tacksam om ni kan berätta.
Du behöver inte ta trianglarna i någon särskild ordning (störst först, etc). Däremot måste du se till att du har samma ordning inom ekvationen du ställer upp. Om det är många olika sidor involverade brukar jag rita pilar som börjar i den ena triangeln (dess sidor blir täljare i bråken) till motsvarande sida i den andra triangeln (dess sidor blir nämnare). Ungefär såhär (varning för ful skiss):
Så länge alla pilar går åt samma håll, och pekar på motsvarande sidor, kommer dina ekvationer att stämma. Detta är särskilt användbart om en triangel ligger ned (så att det är svårare att se likformigheten).
Det spelar ingen roll men man vill gärna sätta den termen som gör uträkningen enklast i nämnaren. I detta fall är det x. Det går fort att ta:
Det ser ut att vara många steg men man gör det fort i huvudet.
Okej grymt, tack!!
Annars är att testa alternativen en snabb metod här när du ställt upp
Man ser ganska lätt att 60 är det enda rimliga när siffrorna är så enkla.
Detta gäller:
Allt kommer ju från "regeln" att när bråk har samma nämnare så kan man addera täljarna över ett gemensamt bråkstreck. Detta är bra att kunna göra bakvägen också.
mrpotatohead skrev:Annars är att testa alternativen en snabb metod här när du ställt upp
Man ser ganska lätt att 60 är det enda rimliga när siffrorna är så enkla.
Detta gäller:
Aah, men exempelvis
Det stämmer ja. De är inte samma.
Tack återigen!!
