reflekterande vågor
I bild 1 har jag försökt rita en våg som reflekteras och bildar en stående våg. I bild 2 har jag sedan ökat frekvensen, men jag förstår inte hur den reflekteras då när den inte hunnit ett hel våglängd.
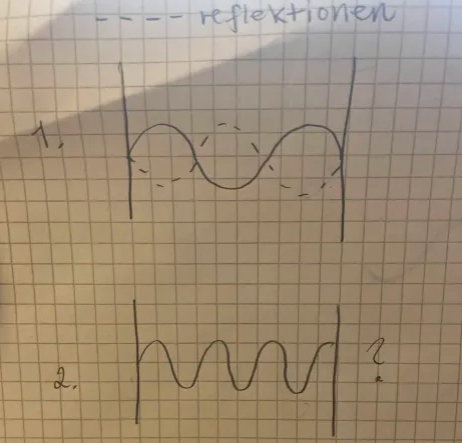
Sedan har jag en till fråga: Om vågen i bild 1 är en stående våg, kommer den att vara det hela tiden eller kommer den också att behöva reflekteras innan den hunnit en hel våglängd som i bild 2. Och har den stående vågen dubbla amplituden jämfört med bild 2?
Den nedre bilden stämmer inte riktigt.
Stående vågor fungerar så att det är noder vid väggarna.
Så är det vid båda väggarna i den övre bilden men bara vid den vänstra väggen i den nedre bilden.
Okej så den nedre bilden är inte en stående våg. Men är då dess amplitud hälften så stor som i den första bilden?
Och kan en stående våg ha en destruktiv interferrens? Jag tänker på den svarta linjen i den här GIF:en när den är platt.
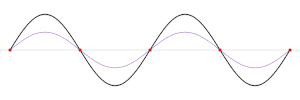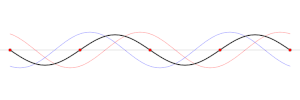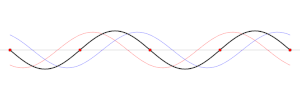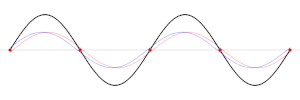
De stående vågorna bildas av de vågor som tillsammans gar en konstruktiv interferens och den stående vägens amplitud är beroende av amplituden hos de vågor som tillsammans skapar den konstruktiva interferensen.
========
För att det ska bildas en stående våg så måste det vara noder vid väggarna.
Om vi säger att avståndet mellan de två väggarna är så är de enda sätten att få stående vågor följande:
- Två noder och en buk. Våglängd :

- Tre noder och två bukar. Våglängd :

- Fyra noder och tre bukar. Våglängd :

- Fem noder och fyra bukar. Våglängd

och så vidare.
Vi kan sammanfatta detta som att de möjliga våglängderna kan vara , där är ett positivt heltal.
Du kan läsa mer om vågor exempelvis här.
Var det svar på dina frågor?
Ja tack så mycket!


