Reducibelt/ irreducibelt polynom
Hej
Jag ska kolla om x^4+4 går att dela upp i faktorer. Jag hänger med såhär långt:
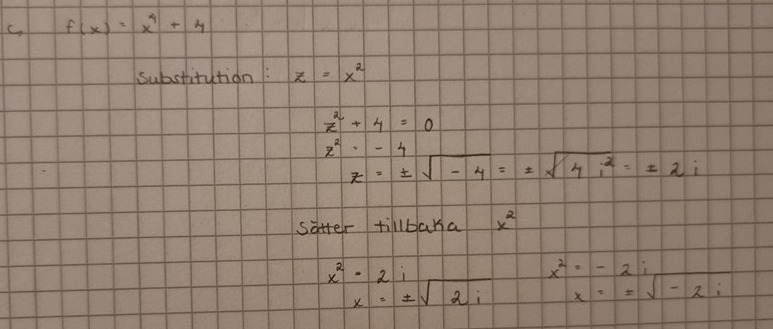
Men hur blir det detta?
![]()
Du har ju kommit fram till alla fyra rötter. Om du tillämpar faktorsatsen kan du skriva om ditt polynom som:
x4+4=(x-√2i)(x+√2i)(x-√-2i)(x+√-2i)
Multiplicera ihop paranteserna med hjälp av konjugatregeln så blir det samma sak som facit.
naytte skrev:Du har ju kommit fram till alla fyra rötter. Om du tillämpar faktorsatsen kan du skriva om ditt polynom som:
x4+4=(x-√2i)(x+√2i)(x-√-2i)(x+√-2i)
Multiplicera ihop paranteserna med hjälp av konjugatregeln så blir det samma sak som facit.
Aha tack, men jag har en till fråga. Vet inte om jag kan ställa den eller om jag måste göra en ny tråd. Men i a och b hade jag x^2+1 och x^4-1. Varför är b också irreducibelt över R? För b kan jag dela upp I termer som innehåller x^2+1

Var står det att b) är irreducibelt över ℝ? Jag tycker det ser väldigt reducibelt ut. Faktoriseringen du har hittat visar väl att det är reducibelt? Det går inte att reducera polynomet till linjära faktorer som alla tillhör ℝ[x], men det verkar ju definitivt gå att reducera över ℝ.
naytte skrev:Var står det att b) är irreducibelt över ℝ? Jag tycker det ser väldigt reducibelt ut. Faktoriseringen du har hittat visar väl att det är reducibelt?
Facit sa att b (x^4-1) ät inte irreducibelt över R, men jag trodde det var irreducibelt över R
Står det någon motivering?
naytte skrev:Var står det att b) är irreducibelt över ℝ? Jag tycker det ser väldigt reducibelt ut. Faktoriseringen du har hittat visar väl att det är reducibelt? Det går inte att reducera polynomet till linjära faktorer som alla tillhör ℝ[x], men det verkar ju definitivt gå att reducera över ℝ.

Det står ju att det inte är irreducibelt.
naytte skrev:Det står ju att det inte är irreducibelt.
Ja, men varför är det inte irreducibelt? Har precis börjat med irreducibelt/ reducibelt så de känns inte 100% naturliga än:/
Du frågade i början av tråden varför polynomet är irreducibelt. Nu har vi kommit fram till att polynomet är reducibelt, alltså inte irreducibelt. Besvarar inte det din fråga?
Polynomet är reducibelt över ℝ eftersom det kan faktoriseras till polynom av lägre grad med reella koefficienter.
naytte skrev:Du frågade i början av tråden varför polynomet är irreducibelt. Nu har vi kommit fram till att polynomet är reducibelt, alltså inte irreducibelt. Besvarar inte det din fråga?
Polynomet är reducibelt över ℝ eftersom det kan faktoriseras till polynom av lägre grad med reella koefficienter.
Vänta så reducibelt betyder att det går att faktorisera tull polynom med lägre grad och inte att det kan skrivas som en produkt av högre grad polynom?
Oj, nu märkte jag felskrivningen på ditt papper i "definitionen" för reducibilitet. Det är omöjligt att faktorisera ett polynom till polyomfaktorer av högre grad.
Så svaret är ja, ett polynom är reducibelt över en kropp K om det går att faktorisera det till polynom av lägre grad vars koefficienter tillhör K. I fallet med reella tal är ett polynom reducibelt över de reella talen om du kan dela upp det i polynomfaktorer vars koefficienter är reella.
naytte skrev:Oj, nu märkte jag felskrivningen på ditt papper i "definitionen" för reducibilitet. Det är omöjligt att faktorisera ett polynom till polyomfaktorer av högre grad.
Så svaret är ja, ett polynom är reducibelt över en kropp K om det går att faktorisera det till polynom av lägre grad vars koefficienter tillhör K. I fallet med reella tal är ett polynom reducibelt över de reella talen om du kan dela upp det i polynomfaktorer vars koefficienter är reella.
Aha okej då är jag med på irreducibel/ reducibel, men jag hänger inte riktigt med på varför man säger över R på a isf
På a är det (x+i)(x-i) och då är det irreducibelt över R för det går inte att faktorisera mer... men borde det inte vara över C för x är i/-i och det tillhör komplexa tal?
Förlåt för så många frågor också🥺🥺
Vad är det du inte förstår i uppgift a)? Du har kommit fram till att de enda polynomfaktorerna som x2+1 har är komplexa. Således är x2+1 irreducibelt över ℝ, men reducibelt över ℂ. I själva verket är alla polynom som tillhör ℝ[x] faktoriserbara i ℂ[x].
Jag tycker att den här artikeln ger en bra förståelse för både begreppen reducibel/irreducibel och begreppet "över", som i "irreducibel över ℝ".
Läs speciellt exemplen.
Aha jag tror jag fattar nu, tack så hemskt mycket för hjälpen😭😭😭😭😭
Eller vänta, varför är inte a och b samma? För b innehåller ju a's två termer (x+i)(x-i)
Som sagt:
Polynomet i b) kan inte faktoriseras upp i linjära polynom som alla tillhör ℝ[x] MEN det finns en polynomfaktorisering av polynomet sådan att alla faktorer tillhör ℝ[x]. Således är polynomet reducibelt över ℝ.
naytte skrev:Som sagt:
Polynomet i b) kan inte faktoriseras upp i linjära polynom som alla tillhör ℝ[x] MEN det finns en polynomfaktorisering av polynomet sådan att alla faktorer tillhör ℝ[x]. Således är polynomet reducibelt över ℝ.
Aha okej, tror jag fattar



