Randvillkor mellan två olika material
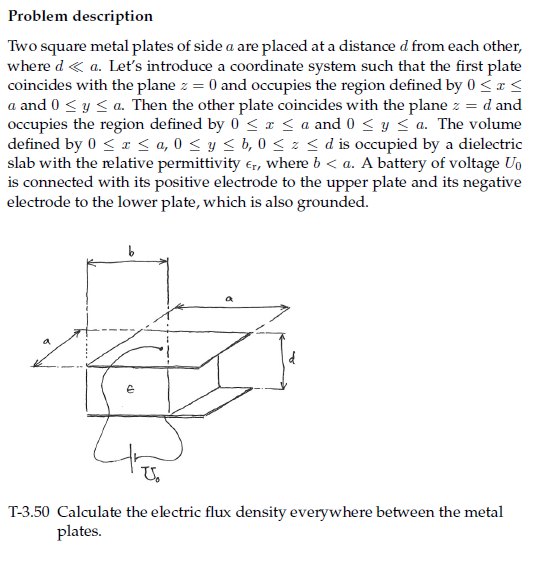
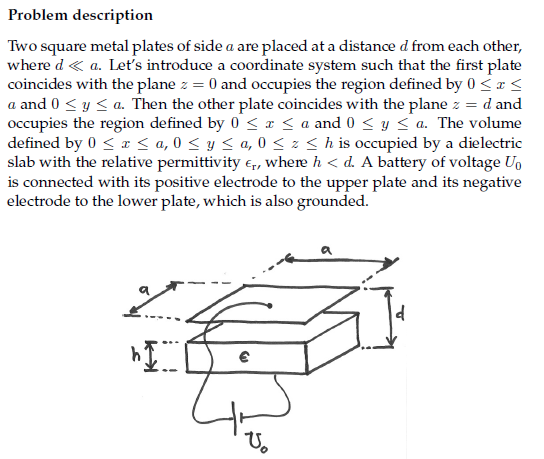
Har lite svårt för de här med randvillkor inom elektrostatiken. Nedan har jag ett problem med en lösning till som jag försöker förstå. Det är ett antal steg jag har hakat upp mig på. Det är tre bilder till lösningarna som jag tyckte blev för kladdigt att ladda upp här, därför finns de här.
Min första fundering är riktningen på det elektriska förskjutningsfältet och , i bild 1 och 2 (lösning) så definierar han z axeln som uppåt, och även riktningen på förskjutningsfältet . Borde inte förskjutningsfältet vara riktat nedåt då det går från plus till minus.
Min andra fråga är, på bild två (lösning) längst ner, där det står "på metallyta:", verkar de undersökas ytterligare ett randvillkor. Hur många ställen ska vi kolla på? Det finns sex möjliga sidor (varav vi undersökt en sida redan) runt om det dielektriska vi kan kolla på. Har inte sett detta tidigare.
Min tredje och sista fråga hänvisar till bild tre (lösning) längst upp. Är detta utvecklingen av det som stod sidan över, dvs ? Om svaret är ja, så tycker jag att och pekar i samma riktning, så varför blir utvecklingen på den tredje sidan längst upp
, tycker det borde vara .
På fråga 1. Man definierar D = .
Här bestäms riktningen av tecknet på skalären Dz. Positivt tecken upp, negativt ner.
På fråga 2. Det viktiga är väl att kolla vad som händer mellan metall och dielektrika. Mellan dielektrika får vi egentligen ingen ny information.
På fråga 3. Se fråga 1. . .
Så D-fältet blir riktat nedåt, som det borde.
PATENTERAMERA skrev:På fråga 1. Man definierar D = .
Här bestäms riktningen av tecknet på skalären Dz. Positivt tecken upp, negativt ner.
På fråga 2. Det viktiga är väl att kolla vad som händer mellan metall och dielektrika. Mellan dielektrika får vi egentligen ingen ny information.
På fråga 3. Se fråga 1. . .
Så D-fältet blir riktat nedåt, som det borde.
Kanon. Tack ska du ha!
PATENTERAMERA skrev:Det viktiga är väl att kolla vad som händer mellan metall och dielektrika.
Det första läraren gör är att kolla vad som händer mellan dielektrika och vad som är (alltså området b<y<a), både ickemetaller, hur går tanken här i så fall?
Man har redan fastslagit att mellan plattorna så är D och E, i varje dielektriskt område, konstanta och parallella med z-axeln. Eftersom det är samma spänning mellan metallplattorna oavsett område så måste E-fältet vara detsamma i båda områdena.
Jag kan därför inte se att vi får någon ny information av randvillkoren mellan de två dielektriska områdena.
PATENTERAMERA skrev:Man har redan fastslagit att mellan plattorna så är D och E, i varje dielektriskt område, konstanta och parallella med z-axeln. Eftersom det är samma spänning mellan metallplattorna oavsett område så måste E-fältet vara detsamma i båda områdena.
Jag kan därför inte se att vi får någon ny information av randvillkoren mellan de två dielektriska områdena.
Det är lite konstigt tycker jag att E-fältet är detsamma på båda områden. Eftersom laddningstätheten är större på den del av metallplattan som täcks av dielektrikan så tycker jag att det verkar logiskt att det elektriska fältet bör vara starkare här. Och eftersom laddningstätheten är lägre där det inte finns dielektrika bör det vara svagare.
Jag gjorde en liknande uppgift, där vi nu hade ett elektriskt förskjutningsfält D och två elektriska fält E. Vi har relationen , så jag tänkte då att båda beror på epsilon, som vi har två av, alltså bör det alltid vara två av varje.
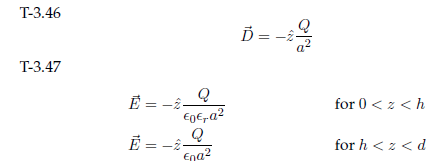
Cien skrev:PATENTERAMERA skrev:Man har redan fastslagit att mellan plattorna så är D och E, i varje dielektriskt område, konstanta och parallella med z-axeln. Eftersom det är samma spänning mellan metallplattorna oavsett område så måste E-fältet vara detsamma i båda områdena.
Jag kan därför inte se att vi får någon ny information av randvillkoren mellan de två dielektriska områdena.
Det är lite konstigt tycker jag att E-fältet är detsamma på båda områden. Eftersom laddningstätheten är större på den del av metallplattan som täcks av dielektrikan så tycker jag att det verkar logiskt att det elektriska fältet bör vara starkare här. Och eftersom laddningstätheten är lägre där det inte finns dielektrika bör det vara svagare.
E-fältet är ju spänning/avstånd. Samma spänning, samma avstånd.
Tänk på att vi bara tagit med den fria ytladdningen på metallplattan. Det finns också en ytladdning pga av polarisation på den övre ytan av dielektrikat.
.
Om du tar med denna borde du komma fram till att det inte finns någon paradox.
Tillägg: 14 dec 2024 21:54

PATENTERAMERA skrev:Cien skrev:PATENTERAMERA skrev:Man har redan fastslagit att mellan plattorna så är D och E, i varje dielektriskt område, konstanta och parallella med z-axeln. Eftersom det är samma spänning mellan metallplattorna oavsett område så måste E-fältet vara detsamma i båda områdena.
Jag kan därför inte se att vi får någon ny information av randvillkoren mellan de två dielektriska områdena.
Det är lite konstigt tycker jag att E-fältet är detsamma på båda områden. Eftersom laddningstätheten är större på den del av metallplattan som täcks av dielektrikan så tycker jag att det verkar logiskt att det elektriska fältet bör vara starkare här. Och eftersom laddningstätheten är lägre där det inte finns dielektrika bör det vara svagare.
E-fältet är ju spänning/avstånd. Samma spänning, samma avstånd.
Tänk på att vi bara tagit med den fria ytladdningen på metallplattan. Det finns också en ytladdning pga av polarisation på den övre ytan av dielektrikat.
.
Om du tar med denna borde du komma fram till att det inte finns någon paradox.
Tillägg: 14 dec 2024 21:54
Jag märkte att man också kan göra på följande sätt.
Vi har
för 0<y<b
för b<y<a
Med sambandet får vi
för 0<y<b
för b<y<a
Här ser vi att de elektriska fälten är identiska, därav endast ett elektriskt fält existerar mellan plattorna.
Ja, vad skönt att det hela hänger i hop oavsett från vilken sida man ser på det.
Tycker själv att detta med polarisation är en ganska subtil sak som kräver en del tankemöda.
PATENTERAMERA skrev:Ja, vad skönt att det hela hänger i hop oavsett från vilken sida man ser på det.
Tycker själv att detta med polarisation är en ganska subtil sak som kräver en del tankemöda.
Ja, tack för all hjälp!


