Randvillkor koaxialkabel

Har två cylindrar med radie a respektive b där b>a och längden L>>b. Mellan ledarna finns luft med permittiviteten $\epsilon=\epsilon_0$. Ett batteri med spänningen U_ab kopplas med den negativa elektroden till den yttre cylinder och den positiva till den inre enligt bild. Efter ett tag har den inre +Q laddning och yttre -Q (när kondensatorn är fulladdad). 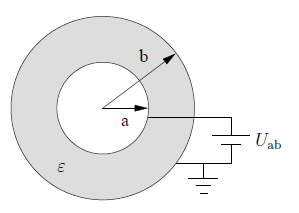Har beräknat det elektriska fältet mellan cylindrarna, potentialen V, laddningen Q till detta (kan vara felberäknat):

$\vec{E}=\dfrac{\rho_s \, a}{\epsilon_0 \, r} \, \hat{r}$ (mellan cylindrarna)

$V \left(r \right)=\dfrac{\rho_s \, a}{\epsilon_0 } \ln{(b/r)}$ då a<r<b

$V\left(b \right)=0$

$V\left(a \right)=\dfrac{\rho_s \, a}{\epsilon_0 } \ln{(b/a)}$

$Q=\dfrac{2 \pi L \epsilon_0}{\ln{(b/a)}} \, U_{ab}$

Nästa del är att kolla om randvillkoren på ytorna av den inre och yttre cylindrarna uppfylls. Det står i uppgiften att jag ska visa detta genom att göra följande tre saker:

Jag tror att jag redan löst den första punkten, då om vi stoppar in r=b i V(r) ovan så får vi att V(b)=0 då vi får ln(1)=0, antar att det är allt som krävs för den.

Lite osäker hur vi gör för de resterande två punkterna.

Om någon kunde förklara vad jag ska göra hade det uppskattas.