Räkna yta under kurva

Hej, 

Du verkar ha ett korrekt uttryck för arean. 

När man letar efter en maximal area letar man efter en maximipunkt för A'(x). Obs: maximipunkt för derivatan!

Vet du hur man hittar sådana?

Tack!

tidigare har det varit att sätta derivatan lika med 0.

jag har försökt sätta A’(x)=0 men fastnar på 0=4x-3x^2

Använd nollproduktsmetoden.

Jag ser att man ska hitta 2 nollpunkter genom att bryta ut x^2 men jag förstår inte hur jag gör med 3 och 4.

Nej, du ska bryta ut endast x. 

Då får du en ekvation som ser ut som denna:

x(4-3x) = 0

Lös den och utvärdera vilken rot som är en maximipunkt.

Tack!

jag för två rötter 

x1= 0 och x2 = 4/3

Sen sätter jag  in x2 = 4/3 i y=2x-x^2  och får y=8/9

aen tänkter jag att jag ska sätta in x och y i triangelns formel A=(b*h)/2?

och då får jag (4/3*8/9)/2 som jag inte förstår hur jag räknar ut.

Har jag ställt upp fel nånstans?

Bra att du fått fram rötterna. 

Sätt inte in tal i formler utan att du förstått varför du gör det, annars blir det fel, vilket det blev nu.

Du har tagit fram två punkter där funktionen har någon typ av extrempunkt. Om vi letar efter en maximipunkt måste alltså en av dessa punkter vara dess x-koordinat.

Vet du hur man kan ta reda på om en punkt är en extrempunkt?

Jag tänkte att x=0 inte kan ge en area vid beräkning så rätt rot måste vara x=4/3, men det kanske är inte är rätt.

jag har gjort andraderivatan nu och får 2 och -2. Men det säger mig inget. Hur ska jag tolka svaret?

Matt3b skrev:

[...]

Kurvan y = 2x - x^2 innesluter tillsammans med x-axeln ett område. Beräkna triangelns maximala area. Svara exakt.

Det område som beskrivs är ingen triangel.

Kan du ladda upp en bild på uppgiften?

Kurvan y = 2x - x^2 innesluter tillsammans med x-axeln ett område. Beräkna triangelns maximala area. Svara exakt.

Jag behöver hjälp att tolka andraderivatan. jag har gjort andraderivatan och får 2 och -2. Men det säger mig inget. Hur ska jag tolka svaret?

eller har jag ställt upp något tidigare i mina uträkningar ?

när jag räknar ut arean A så får jag ((4/3)*(8/9))/2= 16/27. Kan det vara rätt?

jag förstår ändå inte hur jag tolkar andraderivatan.

Yngve skrev:

Matt3b skrev:

[...]

Kurvan y = 2x - x^2 innesluter tillsammans med x-axeln ett område. Beräkna triangelns maximala area. Svara exakt.

Det område som beskrivs är ingen triangel.

Kan du ladda upp en bild på uppgiften?

Vad/var har jag gjort fel?

Vad/var har jag gjort fel?

Kan du samla alla dina beräkningar i en (1) post, det är svårt att greppa över flera svar och dialoger.

så här har jag gjort men är osäker på om det är rätt svar?

hur vet man att andraderivatan ska användas tex?

EDIT - Nu ser jag att du har laddat upp en bild på uppgiften. Missade det tidigare

Matt3b skrev:

så här har jag gjort men är osäker på om det är rätt svar?

hur vet man att andraderivatan ska användas tex?

Det är bra att du samlar allt i en post. Då ser man allt klarare

Triangelns höjd är som du skriver y-värdet, 2x-x^2.

Men den triangel du ritar har inte basen x. x är avståndet till origo VÄNSTER om triangeln.

Om du ser på själva kurvan. Kan du säga när den skär x-axeln?

Om du vet den HÖGRA skärningspunkten, kan du då skriva ett uttryck för basen för din triangel, om den vänstra delen av triangeln ligger på x?

Prova igen och visa räkningar.

Det verkar som att jag likt de andra också missförstod uppgiften. Tänk nästa gång på att lägga i en bild så sparar det vår och din tid!

Som Trinity2 skriver, försökt att skriva uttryck för dessa tre koordinater:

Triangelns högra hörn

Triangelns vänstra hörn

Triangelns topphörn (som ligger på funktionen)

Skriv dessa på formen (x,y) och försök att i största möjliga mån att använda din funktion y(x) till det.

Jag hänger inte med riktigt.

jag tänker att eftersom kurvan går genom origo så kan man lika gärna spegelvända triangeln och att x-koordinaten då blir x eftersom kurvan är en x^2 och symmetrisk?

Matt3b skrev:

Jag hänger inte med riktigt.

jag tänker att eftersom kurvan går genom origo så kan man lika gärna spegelvända triangeln och att x-koordinaten då blir x eftersom kurvan är en x^2 och symmetrisk?

Det är en korrekt observation, tack vare att y(x) är symmetrisk på intervallet. Det ger inte så mycket enklare räkningar dock och man bör vara påpasslig så att man inte alltid tror att denna symmetri föreligger. Man kan t.ex. skapa en x^3-kurva som ser symmetrisk ut, men inte är det.

Men, vi kan köra med din lösning om du vill det, men uppdatera då bilden så vi har något att referera till. Annars blir det svårt. Även din bild på din lösning är felritad i detta fall.

Triangeln i uppgiften är ritad som på min bild så mitt svar är antagligen fel om man ska återge triangelns placering under kurvan med formlerna men jag förstår inte hur man ska beskriva det annars.

Trinity2 skrev:

Matt3b skrev:

Jag hänger inte med riktigt.

jag tänker att eftersom kurvan går genom origo så kan man lika gärna spegelvända triangeln och att x-koordinaten då blir x eftersom kurvan är en x^2 och symmetrisk?

Det är en korrekt observation, tack vare att y(x) är symmetrisk på intervallet. Det ger inte så mycket enklare räkningar dock och man bör vara påpasslig så att man inte alltid tror att denna symmetri föreligger. Man kan t.ex. skapa en x^3-kurva som ser symmetrisk ut, men inte är det.

Men, vi kan köra med din lösning om du vill det, men uppdatera då bilden så vi har något att referera till. Annars blir det svårt. Även din bild på din lösning är felritad i detta fall.

Triangeln i uppgiften är ritad som på min bild så mitt svar är antagligen fel om man ska återge triangelns placering under kurvan med formlerna men jag förstår inte hur man ska beskriva det annars.

Vi tar det metodiskt i bitar. Det löser 99.99% av denna typ av uppgift.

1. Rita rätt bild - Klart

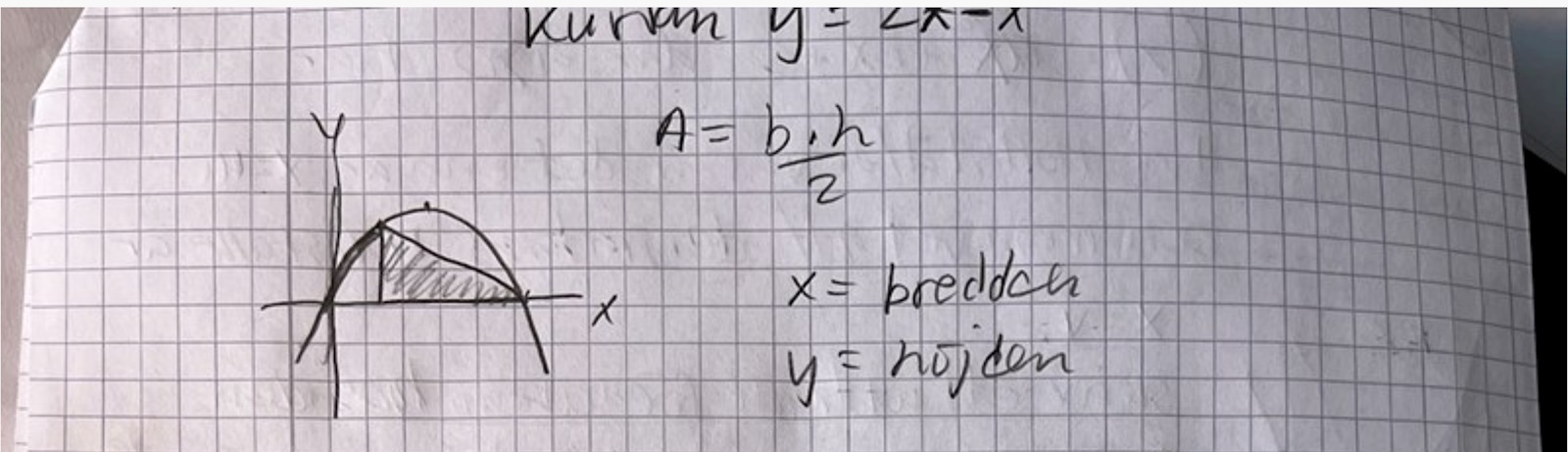
2. Sätt ut viktiga punkter.

Nollställen är viktiga. Varför skriver du inte ut dem i bilden. Det blir abstrakt och "luddigt" vad bilden visar.

Vilka är nollställena?

Vad är det för kurva du ritat? Varför inte skriv ut det i bilden, så vi vet vad som gäller?

3. Låt det vänstra nedre hörnet ha koordinaten (x,0).

4. Uttryck basens längd med hjälp av x.

5. Uttryck höjdens längd med hjälp av ... ja... vad?

Gör detta först, så räknar vi vidare senare.

Det är det här jag kör fast på, att uttrycka basen.

(x,0) och (x+b,0)?

eller ska jag köra pq-formeln och få fram rötterna?

Matt3b skrev:

Det är det här jag kör fast på, att uttrycka basen.

(x,0) och (x+b,0)?

eller ska jag köra pq-formeln och få fram rötterna?

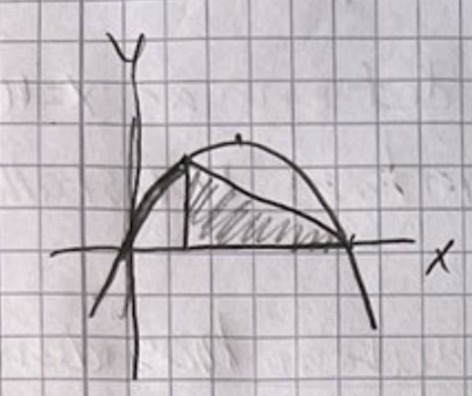
Vad är nollställen - skriv ut dem.

Triangelns vänstra punkt sätter vi till x. Hur lång är då basen?

Ja de är (0,0) och (x,0) tänker jag men jag förstår inte hur jag ska få fram den delen som är till höger om x om jag låter vänstra hörnet på triangeln vara x.

Matt3b skrev:

[...] men jag förstår inte hur jag ska få fram den delen som är till höger om x om jag låter vänstra hörnet på triangeln vara x.

Ledtråd: Längden av triangelns bas är då lika med avståndet mellan punkterna (x, 0) och (2,0).

Jag hänger inte med? Måste man använda pq-formeln för att få punkten x=2. Är det enda sättet att få fram basen?

Du behöver inte använda pq-formeln.

Totta på min bild. Vad är avståndet mellan de två givna punkterna?

Om du inte ser det direkt kan du ju använda avståndsformeln, men det är lite overkill.

2-1=1?

men jag förstår inte hur man får fram koordinaten (2,0)

Matt3b skrev:

2-1=1?

men jag förstår inte hur man får fram koordinaten (2,0)

Det är ett av nollställena för 2x-x².

Du kan hitta dem genom att lösa ekvationen 0 = 2x-x²

Efter faktorisering: 0 = x(2-x)

Nollproduktmetoden ger dig nu de två nollställena x = 0 och x = 2.

Det här var krångligare än jag trott.

måste man inte använda pq-formeln för att få ut rötterna, dvs nollställen?

Och sen hur får man basen förstår jag ändå inte. 

Så basen är 2-x?

Matt3b skrev:

Så basen är 2-x?

Ja

Är då arean A= ((2-x)(2x-x^2))/2?

Matt3b skrev:

[...]

måste man inte använda pq-formeln för att få ut rötterna, dvs nollställen?

[...]

Du kan, men måste inte, använda pq-formeln.

Matt3b skrev:

Är då arean A= ((2-x)(2x-x^2))/2?

Ja, det stämmer.

Okej, nästa steg är isåfall att derivera areans uttryck för att få maximipunkten och det blir en väldigt svår ekvation?

A=(4x^2-x^3-4x)/2 med derivatan A’=(8x-3x^2-4)/2? och sätter den =0

hur löser jag den? Har jag ställt upp fel från början?

Det är rätt, förutom att du har fått fel tecken på uttrycket.

Det ska vara A(x) = (x³-4x²+4x)/2 med derivata A'(x) = (3x²-8x+4)/2.

Ekvationen A'(x) = 0 löser du sedan med hjälp av kvadratkomplettering eller pq-formeln.

Om du vill kan du behålla A(x) i 'faktorform' och inte utveckla den. Räkningarna blir lite enklare och speciellt ekvationen på slutet

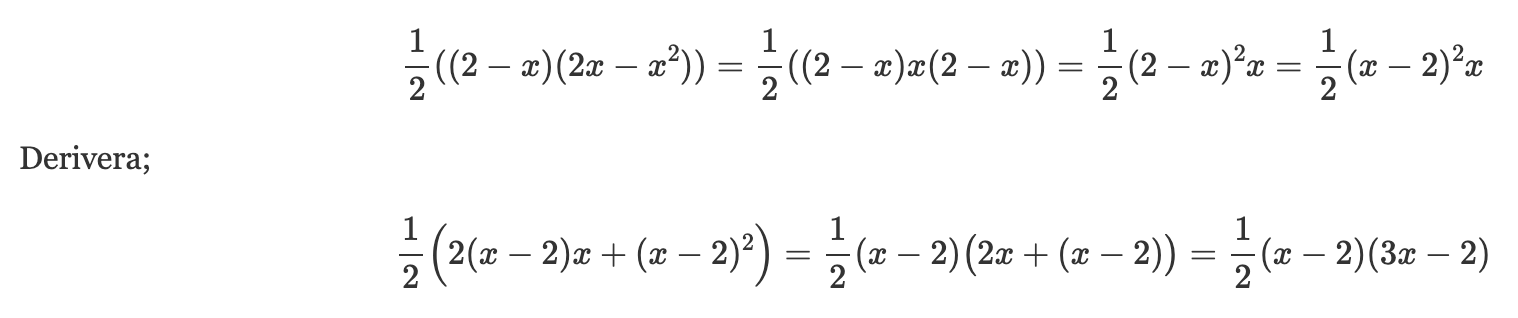
Sedan löser du ekvationen lätt, nästan i huvudet.

Efter mycket om och men tror jag att jag har en lösning, kan detta stämma? Är det rätt? Eller har jag gjort det för krångligt?

Matt3b skrev:

Efter mycket om och men tror jag att jag har en lösning, kan detta stämma? Är det rätt? Eller har jag gjort det för krångligt?

Här ligger arbete bakom detta! Ser bra ut. Men, x=2. Vad betyder det för triangeln? Hur ser den ut då? Är det lönt att ta hänsyn till det svaret?

Lärare brukar älska dra poäng för utebliven enhet så tag en varm synål och lite sot och tatuera in på insidan på ögonlocken att alltid svara med enhet. Retligt att missa 1p för en enkel sak.

Ja areaenheter! a.e ska det vara.

men x=2 är väl för att få ut koordinaten för att kunna göra uttrycket för basen. Eller är det något mer den ska användas till? Figuren är avritad från uppgiften.

Matt3b skrev:

Ja areaenheter! a.e ska det vara.

men x=2 är väl för att få ut koordinaten för att kunna göra uttrycket för basen. Eller är det något mer den ska användas till? Figuren är avritad från uppgiften.

x=2 innebär att triangelns vänstra sida;

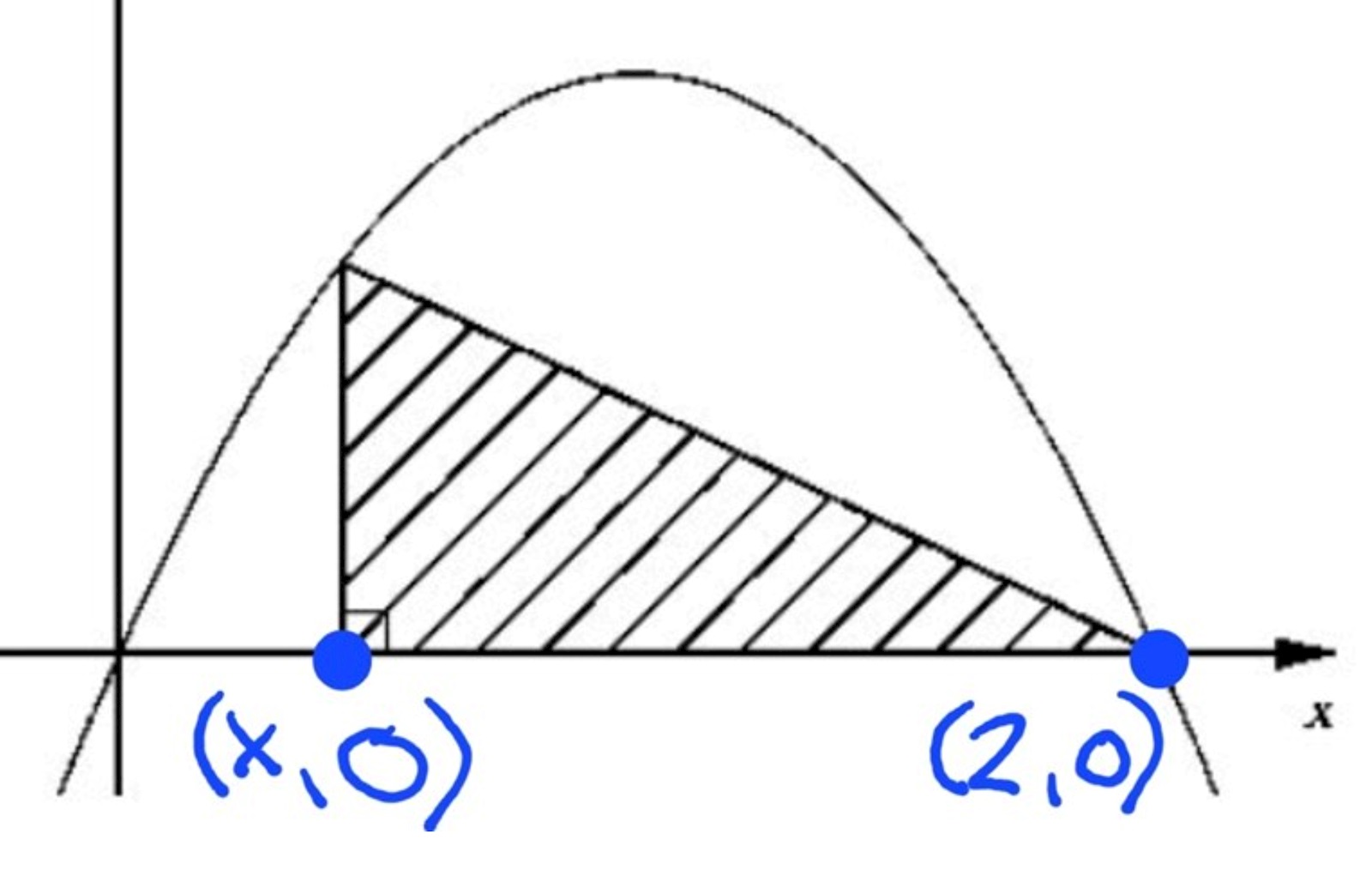
ligger på det högra hörnet - inte mycket av triangel kvar :)

Jag funderar men som jag tänker är  x=2 punkten där triangeln börjar?

Tack för hjälp!

Matt3b skrev:

Jag funderar men som jag tänker är  x=2 punkten där triangeln börjar?

Tack för hjälp!

Dt är helt rätt, x = där den börjar. Men om nu x=2, var börjar den då? Och var slutar den?

Ja som jag tänker börjar den inte alls. Om x är lika med 2 och basen på triangeln är 2-x så finns inte triangeln och då tänker jag att basen inte skulle vara 2-x? Jag hänger nog inte med.

Matt3b skrev:

Ja som jag tänker börjar den inte alls. Om x är lika med 2 och basen på triangeln är 2-x så finns inte triangeln och då tänker jag att basen inte skulle vara 2-x? Jag hänger nog inte med.

Du tänker rätt. x=2 = finns ingen triangel. x=2 är en lösning som inte duger och som du direkt kan förkasta. Kvar blir bara x=2/3 som du måste verifiera att det är ett maximum, viilket du gjorde bra.

När man börjar med denna typ av uppgifter är det ALLTID att rekommendera att man funderar på vad x kan vara.

Du skriver tidigt att

 A= ((2-x)(2x-x^2))/2

och då ser man extra noga på bilden och tänker "Hm... VAD exakt kan x variera mellan för att det skall bli en triangel..... x=0 ger ingen triangel, den har ingen höjd och finns den inte.... oh x=2 är samma sak, ingen höjd här heller = triangel finns inte.... men alla x mellan 0 och 2 funkar...." och så skriver man

 A= ((2-x)(2x-x^2))/2,    OBS! 0<x<2

Då vet man det! Sedan när du räknar på så kommer du fram till något x senare och du ser du på vad du skrev från starten och kan direkt förkasta orimliga x. Det spar du tid på och räkningar och jobb. FÖrsök finna så mycket fakta du kan från bilden. Det kräver ofta inga beräkningar och spar dig kanske 10 minuter senare, beroende på hur snabb du är på räkning och "aldrig räknar fel" (vilket alla gör...). Räkna inte på saker som inte behövs räknas - tar tid, kan bli fel och kan därmed ge fel slutsatser och fel svar.

Jag förstår vad du menar, jag hade kunnat hoppa över att räkna A’’(2) (under förutsättning att jag räknar rätt på A’’(2/3). 
Intervallet var bra tips!

Matt3b skrev:

Jag förstår vad du menar, jag hade kunnat hoppa över att räkna A’’(2) (under förutsättning att jag räknar rätt på A’’(2/3). 
Intervallet var bra tips!

Exakt. Ju mindre du räknar, ju färre fel, ju färre felaktiga slutsatser. Säg att du genom fel fått A''(2)<0, då hade du sagt att det också var ett maxima kanske. Man skall inte öppna dörrar som inte behövs öppnas.