räkna ut fyrhörningens area
Om diagonalerna i en fyrhörning är vinkelräta mot varandra och är 4 längd- enheter respektive 5 längdenheter långa, så är fyrhörningens area
(a) 20 a.e.; (b) 10 a.e.; (c) annat tal; (d) kan ej avgöras.
svar B
ingen aning hur jag ska räkna ut det här.
Rita! Om diagonalerna är vinkelräta måste vi ha att göra med någon slags drakformat objekt:
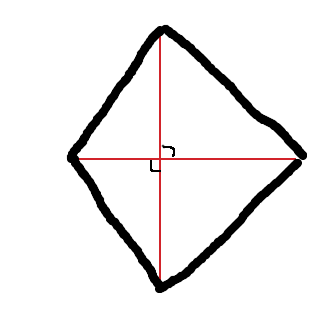
Vilken area har denna figur (om diagonalerna har måtten du skrivit)?
Smutstvätt skrev:Rita! Om diagonalerna är vinkelräta måste vi ha att göra med någon slags drakformat objekt:
Vilken area har denna figur (om diagonalerna har måtten du skrivit)?
ingen aning, det går väl inte ens använda pythagoras? för vi vet ju inte vart exakt diagonalerna korsar. Det enda vi vet är att de är vinkelräta mot varandra
Tänk dig att du viker ut flikarna. Då får du en rektangulär figur i stil med denna:
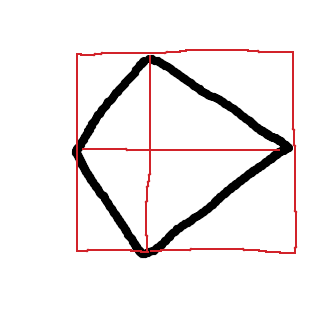
Det är en rektangel, med sidlängderna 4 och 5, och den är exakt dubbelt så stor som figuren vi hade innan. :)
Smutstvätt skrev:Tänk dig att du viker ut flikarna. Då får du en rektangulär figur i stil med denna:
det går ju fortfarande inte räkna ut det svartsträckade?
Mycket riktigt, men vi behöver inte räkna ut de svarta sträckorna. Det enda vi behöver beräkna är hur stor area de innesluter, och den arean är precis hälften så stor som arean av rektangeln den är inskriven i.
Smutstvätt skrev:Mycket riktigt, men vi behöver inte räkna ut de svarta sträckorna. Det enda vi behöver beräkna är hur stor area de innesluter, och den arean är precis hälften så stor som arean av rektangeln den är inskriven i.
hur vet man att den är precis hälften?
Diagonalerna utgör två kateter till en rätvinklig triangel. Du har triangeln ABC, låt AB vara 5l.e och BC 4l.e arean blir
Det blir hälften, eftersom vi tar varje triangel (de fyra i mitten), kopierar dem, och sätter på utsidan, så att vi får en rektangel. Vi började med fyra olika trianglar, och nu har vi två uppsättningar av samma fyra trianglar.


