Räkna arean mellan två grafer
Figuren nedan visar parabeln f(x)=x2 och linjen g(x)=4x−4. Linjen tangerar parabeln i punkten P. Parabeln och linjen innesluter tillsammans med xx-axeln ett område som skuggats i figuren.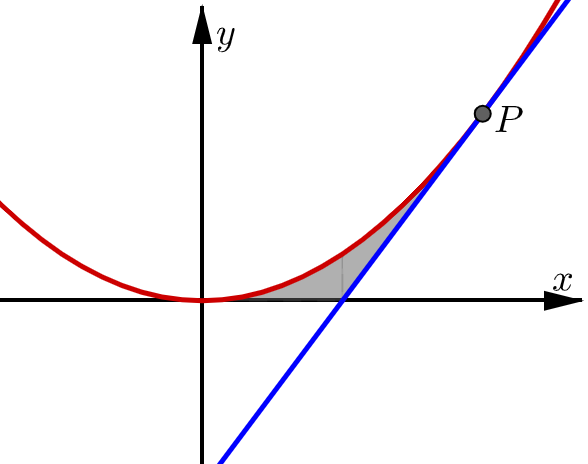
Bestäm arean av det skuggade området.
Jag la in det såhäe i exam: integral(x2-4x+4) från 0 till 2. Då får jag 8/3 men i facit står det 2/3 och dem löser det genom att räkna ut areorna enskilda och sedan subtraherar dem. Är inte det sättet jag har gjort rätt också? Alltså arean mellan två kurvor blir ju integralen (kurvan ovanpå - kurvan under)
Hej.
Det du har beräknat är arean av det område som begränsas av den röda grafen, den blåa grafen och y-axeln.
Du har alltså även räknat med triangeln under x-axrln.
Yngve skrev:Hej.
Det du har beräknat är arean av det område som begränsas av den röda grafen, den blåa grafen och y-axeln.
Du har alltså även räknat med triangeln under x-axrln.
borde inte integralen blivit negativ då arean där under är större?
Nej, när du integrerar "övre funktionen" minus "undre funktionen" så blir resultatet alltid positivt, oavsett var i förhållande till x-axeln graferna ligger.
Men om du integrerar "undre funktionen" minus "övre funktionen" så blir resultatet alltid negativt, oavsett var i förhållande till x-axeln graferna ligger.
=======
Du tänker nog på när man integrerar en funktion f(x), vars graf ligger helt eller delvis under x-axeln.
Då gäller samma sak som ovan, fast den andra funktionen är då g(x) = 0, vars graf ju sammanfaller med x-axeln.
Du integrerar alltså egentligen inte f(x) utan istället f(x) - g(x), dvs f(x) - 0, dvs f(x).
Det är därför de delar av funktionen som är
- större än 0 ger ett positivt bidrag till integralen, eftersom f(x) där är den övre funktionen och g(x) den undre funktionen.
- mindre än 0 ger ett negativt bidrag till integralen, eftersom f(x) där är den undre funktionen och g(x) den övre funktionen.
